标签:建模 dict 原则 脏数据 das 关系 添加 rip use
目录
??当我们得到数据后,接下来就是要考虑样本数据集的数据和质量是否满足建模的要求?是否出现不想要的数据?能不能直接看出一些规律或趋势?每个因素之间的关系是什么?
??通过检验数据集的数据质量,绘制图表,计算某些特征值等手段,对样本数据集的结构和规律进行分析的过程就是数据探索。数据质量检测对后面的数据预处理有很大参考作用,并有助于选择合适的建模方法。
??数据探索大致分为 质量探索 和 特征探索 两方面。
?? 定义:数据质量分析是数据预处理的前提,也是对数据挖掘的结果有效性和准确性的保证,只有拥有可信的数据,才能够构建准确的模型。
??主要任务: 检测是否存在脏数据(不符合要求与不能方便地进行分析的数据)。包括缺失的数据,异常的数据,不一致的数据,以及含有其他不标准符号以及重复的数据。
??数据的缺失主要包括 记录的缺失 和 记录中某个字段的缺失 。他们都会造成分析结果的不准确。
??产生原因是一些信息无法获取或者在收集获取的时候出现了遗漏或者设计的时候的一些值在获取的时候并没有。
??数据缺失会丢失大量有用信息,或者造成建模混乱,得到的模型不准确,规律难以得到。
??使用简单的统计分析,可以得到含有缺失值的属性的个数,以及缺失数,缺失率等。
??异常值分析是检验数据是否有录入错误以及含有不合常理的数据。通过检测数据是否有异常,发现问题并而找到改进的策略。
??异常值是指样本中的个别值,数值明显偏离其余的观测值,故又叫离群值。
??分析步骤:
??(1)简单统计量分析
??首先可以通过一些常见的检测值对变量做一个探索,查看哪些数据是不合情理的。比如用最大值和最小值,和实际的的现实意义联系判断变量取值是否合理。
??(2)正态分布原则
??正态分布原则就是异常值被定义为一组测试值中与平均值的偏差超过三倍标准差的值。
??(3)箱型图分析
??箱型图提供的一个识别异常值的一个标准,异常值通常被定义为小于Ql - 1.5IQR或大于Qu + 1.5IQR的值。Ql称为下四分位数,表示样本值中有四分之一
比它小;Qu成为上四分位数,表示样本值中有四分之一比它大;IQR是四分位数间距,是QI和Qu的差,包括全部样本的一半。
??实例:
??这里我们首先先爬取华为手机日销量数据,如下:
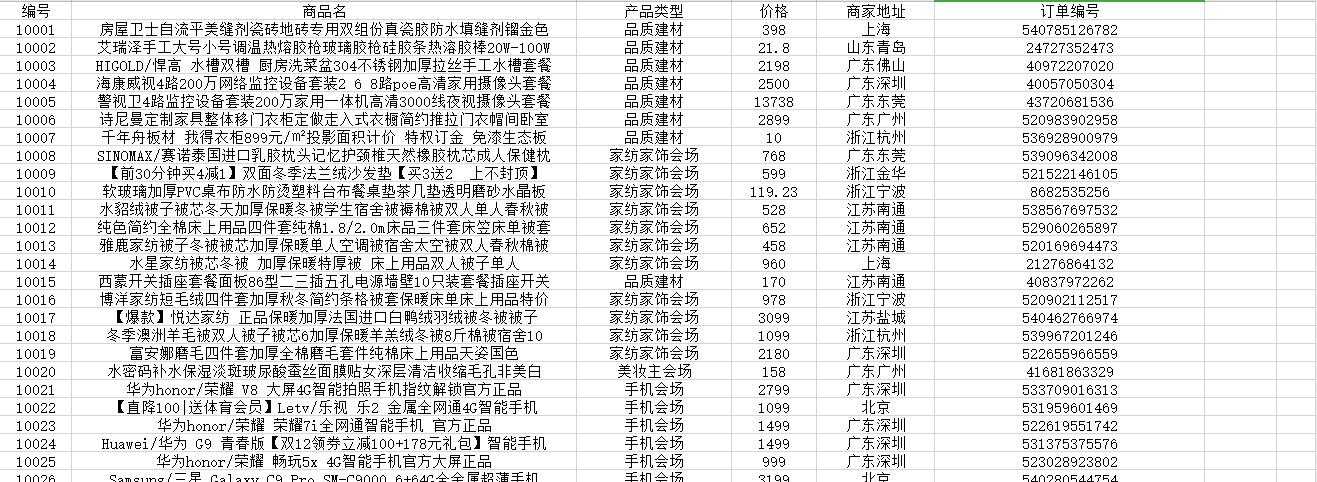

??我们规定商品的价格的平均值前后一定范围价格为正常值,来分析所有商品的价格情况。
??但是有些数据是缺失的,而且数据多的时候人工识别不出,可以用程序
检测含有缺失值的记录和属性以及个数,来求缺失率。
??数据的基本情况:
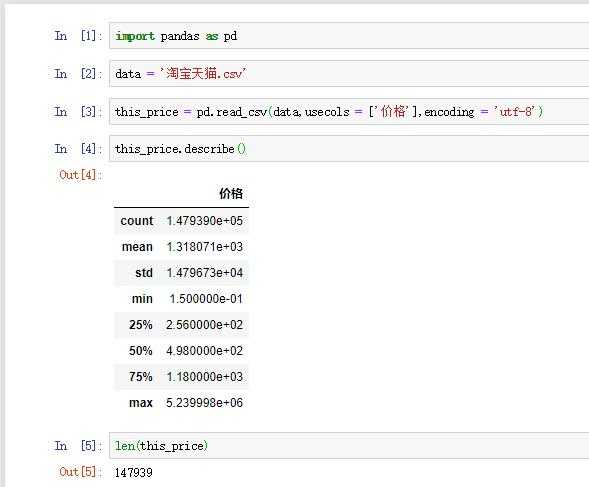
??这里可以看到数据一共有147939条,还可以得到平均值(mean),标准差(std),最小值(min),最大值(max)以及四分位数等。
??下面可以用箱型图检测异常值。
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
data = '淘宝天猫.csv'
this_price = pd.read_csv(data,usecols = ['价格'],encoding = 'utf-8')
plt.figure() # 建立图像
p = this_price.boxplot(return_type='dict')
x = p['fliers'][0].get_xdata()
y = p['fliers'][0].get_ydata()
y.sort()
# 用annotate添加注释
for i in range(len(x)):
if i > 0:
plt.annotate(y[i],xy = (x[i],y[i]), xytext = (x[i] + 0.05 - 0.8 / (y[i] - y[i - 1]),y[i]))
else:
plt.annotate(y[i],xy = (x[i],y[i]), xytext = (x[i] + 0.08,y[i]))
plt.show()??之前未处理的图片
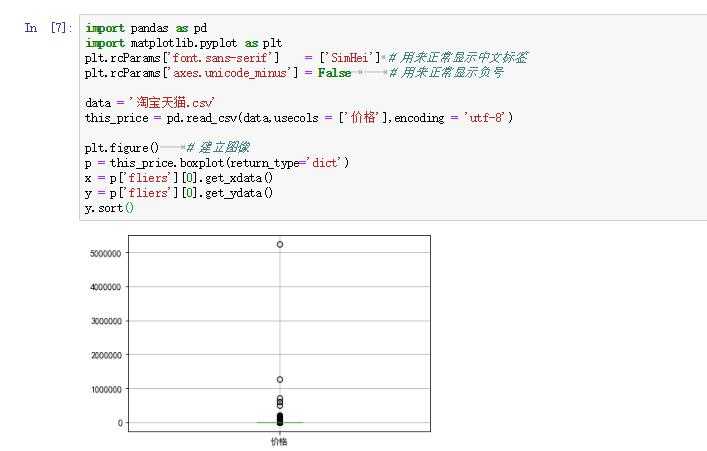
??处理后的图片
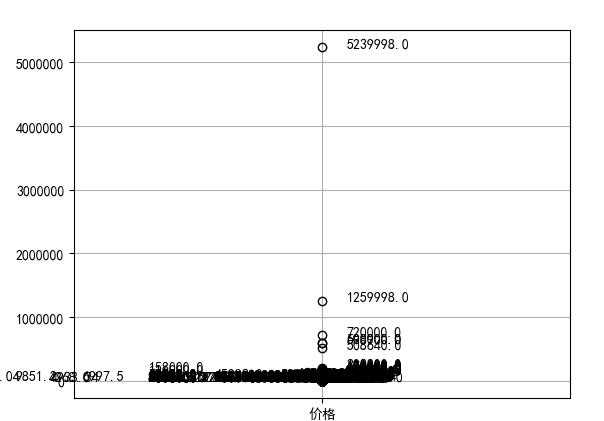
可以根据不同的需求进行调节,然后按照不同规则进行选取和分析数据。
??数据不一致是指数据的矛盾性,不相容性,可能有不同表之间的联系,然后改变了其他表但并未改变与之相连的表。
标签:建模 dict 原则 脏数据 das 关系 添加 rip use
原文地址:https://www.cnblogs.com/ITXiaoAng/p/11889811.html