使用场景:
1,空间复杂度 越低越好、n值较大:
堆排序 O(nlog2n) O(1)
2,无空间复杂度要求、n值较大:
桶排序 O(n+k) O(n+k)
经典排序算法图解:
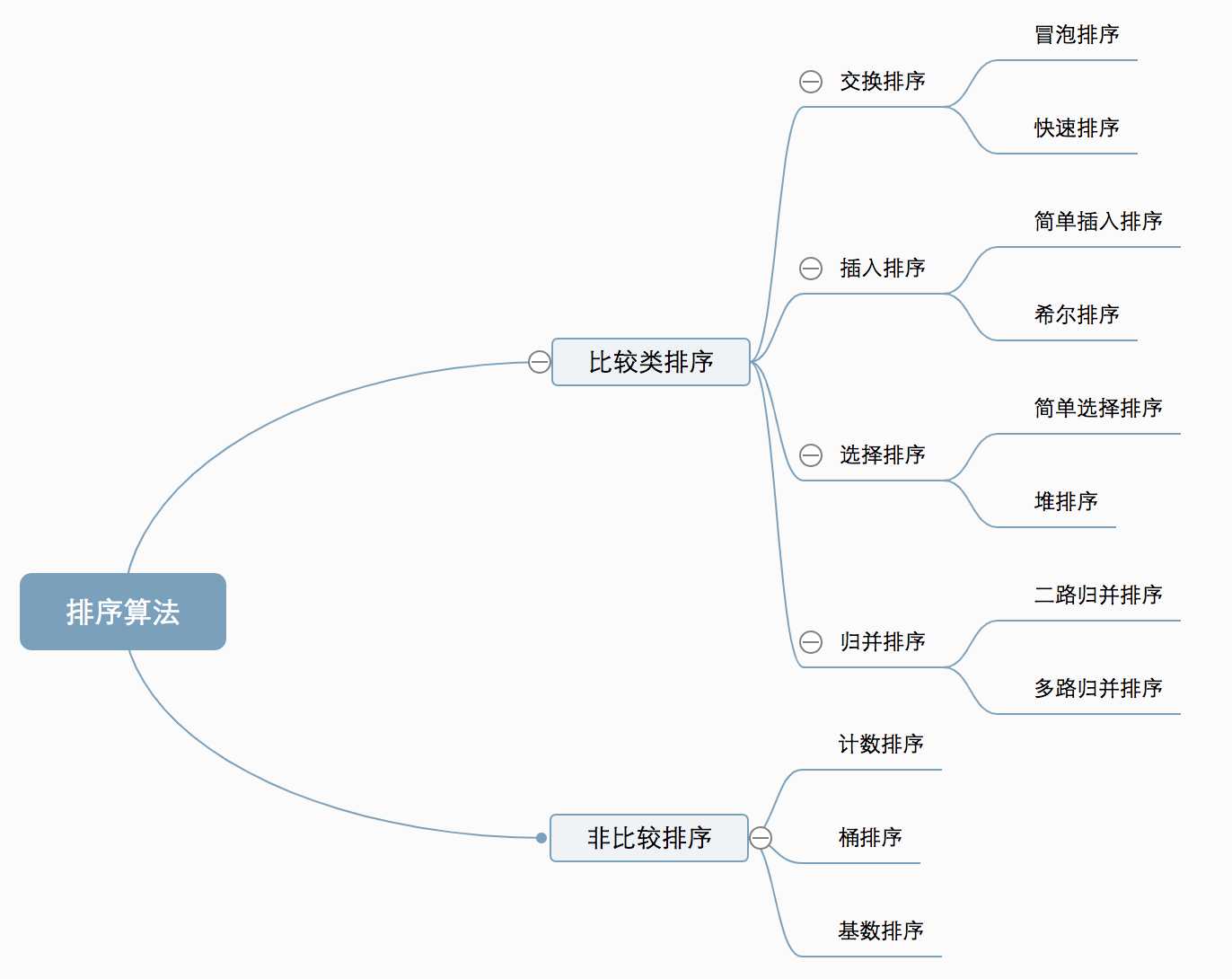
经典排序算法的复杂度:
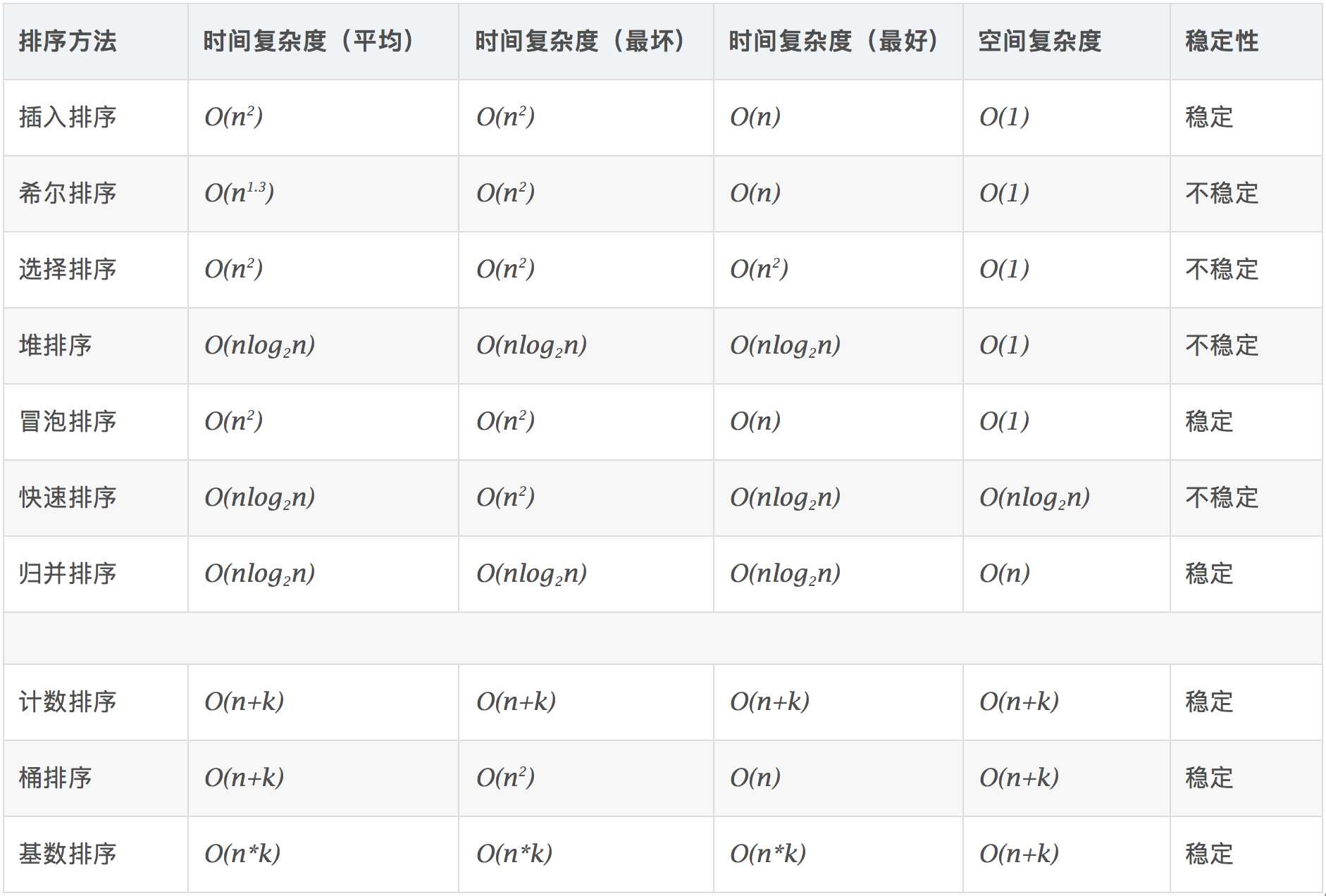
大类一(比较排序法):
1、冒泡排序(Bubble Sort)【前后比较-交换】
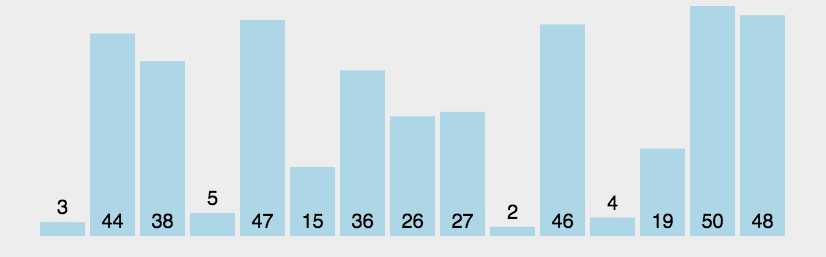
python代码实现:
1 d0 = [2, 15, 5, 9, 7, 6, 4, 12, 5, 4, 2, 64, 5, 6, 4, 2, 3, 54, 45, 4, 44] 2 d0_out = [2, 2, 2, 3, 4, 4, 4, 4, 5, 5, 5, 6, 6, 7, 9, 12, 15, 44, 45, 54, 64] # 正确排序 3 4 while 1: 5 state = 0 # 假设本次循环没有改变 6 for i in range(len(d0) - 1): 7 if d0[i] > d0[i + 1]: 8 d0[i], d0[i + 1] = d0[i + 1], d0[i] 9 state = 1 # 有数值交换,那么状态值置1 10 if not state: # 如果没有数值交换,那么就跳出 11 break 12 13 print(d0) 14 print(d0_out)
2、选择排序(Selection Sort)【选择最小的数据放在前面】
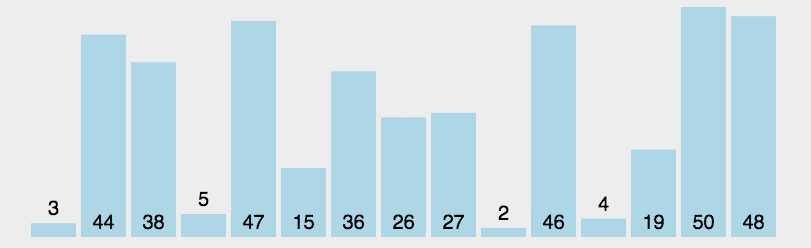
python代码实现:
1 def select_sort(data): 2 d1 = [] 3 while len(data): 4 min = [0, data[0]] 5 for i in range(len(data)): 6 if min[1] > data[i]: 7 min = [i, data[i]] 8 del data[min[0]] # 找到剩余部分的最小值,并且从原数组中删除 9 d1.append(min[1]) # 在新数组中添加 10 return d1 11 12 if __name__ == "__main__": 13 d0 = [2, 15, 5, 9, 7, 6, 4, 12, 5, 4, 2, 64, 5, 6, 4, 2, 3, 54, 45, 4, 44] # 原始乱序 14 d0_out = [2, 2, 2, 3, 4, 4, 4, 4, 5, 5, 5, 6, 6, 7, 9, 12, 15, 44, 45, 54, 64] # 正确排序 15 d1 = select_sort(d0) 16 print(d1) 17 print(d0_out)
3、插入排序(Insertion Sort)【逐个插入到前面的有序数中】
直接插入排序-python实现:
1 def direct_insertion_sort(d): # 直接插入排序,因为要用到后面的希尔排序,所以转成function 2 d1 = [d[0]] 3 for i in d[1:]: 4 state = 1 5 for j in range(len(d1) - 1, -1, -1): 6 if i >= d1[j]: 7 d1.insert(j + 1, i) # 将元素插入数组 8 state = 0 9 break 10 if state: 11 d1.insert(0, i) 12 return d1 13 14 15 if __name__ == "__main__": 16 d0 = [2, 15, 5, 9, 7, 6, 4, 12, 5, 4, 2, 64, 5, 6, 4, 2, 3, 54, 45, 4, 44] # 原始乱序 17 d0_out = [2, 2, 2, 3, 4, 4, 4, 4, 5, 5, 5, 6, 6, 7, 9, 12, 15, 44, 45, 54, 64] # 正确排序 18 d1 = direct_insertion_sort(d0) 19 print(d1) 20 print(d0_out)
折半插入排序-python实现:
1 d0 = [2, 15, 5, 9, 7, 6, 4, 12, 5, 4, 2, 64, 5, 6, 4, 2, 3, 54, 45, 4, 44] # 原始乱序 2 d0_out = [2, 2, 2, 3, 4, 4, 4, 4, 5, 5, 5, 6, 6, 7, 9, 12, 15, 44, 45, 54, 64] # 正确排序 3 4 d1 = [d0[0]] 5 del d0[0] 6 7 for i in d0: 8 index_now = [0, len(d1)] 9 while 1: 10 index = index_now[0] + int((index_now[1] - index_now[0]) / 2) 11 if i == d1[index]: 12 d1.insert(index+1,i) 13 break 14 elif index in index_now: # 如果更新的index值在index_now中存在(也有可能是边界),那么就表明无法继续更新 15 d1.insert(index+1,i) 16 break 17 elif i > d1[index]: 18 index_now[0] = index 19 elif i < d1[index]: 20 index_now[1] = index 21 22 print(d1) 23 print(d0_out)
4、希尔排序(Shell Sort)【从大范围到小范围进行比较-交换】类似冒泡和插入的联合
python代码实现:
1 def direct_insertion_sort(d): # 直接插入排序,因为要用到后面的希尔排序,所以转成function 2 d1 = [d[0]] 3 for i in d[1:]: 4 state = 1 5 for j in range(len(d1) - 1, -1, -1): 6 if i >= d1[j]: 7 d1.insert(j + 1, i) # 将元素插入数组 8 state = 0 9 break 10 if state: 11 d1.insert(0, i) 12 return d1 13 14 15 def shell_sort(d): # d 为乱序数组,l为初始增量,其中l<len(d),取为len(d)/2比较好操作。最后还是直接省略length输入 16 length = int(len(d) / 2) # 10 17 num = int(len(d) / length) # 2 18 while 1: 19 20 for i in range(length): 21 d_mid = [] 22 for j in range(num): 23 d_mid.append(d[i + j * length]) 24 d_mid = direct_insertion_sort(d_mid) 25 for j in range(num): 26 d[i + j * length] = d_mid[j] 27 # print(d) 28 length = int(length / 2) 29 if length == 0: 30 return d 31 break 32 # print(‘length:‘,length) 33 num = int(len(d) / length) 34 35 36 if __name__ == "__main__": 37 d0 = [2, 15, 5, 9, 7, 6, 4, 12, 5, 4, 2, 64, 5, 6, 4, 2, 3, 54, 45, 4, 44] # 原始乱序 38 d0_out = [2, 2, 2, 3, 4, 4, 4, 4, 5, 5, 5, 6, 6, 7, 9, 12, 15, 44, 45, 54, 64] # 正确排序 39 d1 = shell_sort(d0) 40 print(d1) 41 print(d0_out)
5、归并排序(Merge Sort)【分治法-2-4-8插入排序】
python代码实现(这个地方是由大往小进行递归):
1 # 归并排序,还有些问题。其中有些细节需要重新理解 2 # 也是递归问题 3 def merge_sort(data): # 分治发的典型应用,大问题拆分成小问题,逐个击破,之后将结果合并 4 half_index = int(len(data) / 2) # 将数组拆分 5 6 d0 = data[:half_index] 7 d1 = data[half_index:] 8 9 if len(d0) > 1: 10 d0 = merge_sort(d0) 11 12 if len(d1) > 1: 13 d1 = merge_sort(d1) 14 15 index = 0 16 for i in range(len(d1)): 17 state = 1 18 for j in range(index, len(d0)): 19 if d1[i] < d0[j]: 20 state = 0 21 index = j + 1 22 d0.insert(j, d1[i]) 23 break 24 if state == 1: # 如果大于d0这个队列的所有值,那么直接extend所有数据 25 d0.extend(d1[i:]) 26 break 27 return d0 28 29 30 if __name__ == "__main__": 31 d0 = [2, 15, 5, 9, 7, 6, 4, 12, 5, 4, 2, 64, 5, 6, 4, 2, 3, 54, 45, 4, 44] # 原始乱序 32 d0_out = [2, 2, 2, 3, 4, 4, 4, 4, 5, 5, 5, 6, 6, 7, 9, 12, 15, 44, 45, 54, 64] # 正确排序 33 d1 = merge_sort(d0) 34 print(d1) 35 print(d0_out)
python代码实现(由小扩展到大的子序列):
1 2 def list_sort(d0, d1): # 基元组往大扩展 3 index = 0 4 for i in range(len(d1)): # 遍历d1数组 5 state = 1 6 for j in range(index, len(d0)): # 遍历d0数组 7 if d0[j] > d1[i]: 8 state = 0 9 index = j + 1 10 d0.insert(j, d1[i]) 11 break 12 if state == 1: # 如果大于d0这个队列的所有值,那么直接extend所有数据 13 d0.extend(d1[i:]) 14 break 15 return d0 16 17 18 def merge_sort(data): 19 d0 = [[x] for x in data] 20 while len(d0) != 1: # 循环条件 21 length = len(d0) 22 half = int(length/2) # 除2的整数部分 23 quo = length%2 # 除2的商 24 d0_mid = [] 25 for i in range(half): 26 d0_mid.append(list_sort(d0[i*2], d0[i*2+1])) 27 if quo: 28 d0_mid.append(d0[-1]) 29 d0 = d0_mid 30 31 return d0[0] 32 33 34 35 if __name__ == "__main__": 36 d0 = [2, 15, 5, 9, 7, 6, 4, 12, 5, 4, 2, 64, 5, 6, 4, 2, 3, 54, 45, 4, 44] # 原始乱序 37 d0_out = [2, 2, 2, 3, 4, 4, 4, 4, 5, 5, 5, 6, 6, 7, 9, 12, 15, 44, 45, 54, 64] # 正确排序 38 d1 = merge_sort(d0) 39 print(d1) 40 print(d0_out)
6、快速排序(Quick Sort)【选取一个基准值,小数在左大数在在右】
python代码实现:
1 # import sys 2 # sys.setrecursionlimit(1000000) 3 4 def quick_sort(data): 5 d = [[], [], []] 6 d_pivot = data[-1] # 因为是乱序数组,所以第几个都是可以的,理论上是一样的 7 for i in data: 8 if i < d_pivot: # 小于基准值的放在前 9 d[0].append(i) 10 elif i > d_pivot: # 大于基准值的放在后 11 d[2].append(i) 12 else: # 等于基准值的放在中间 13 d[1].append(i) 14 15 # print(d[0], d[1], d[2]) 16 if len(d[0]) > 1: # 大于基准值的子数组,递归 17 d[0] = quick_sort(d[0]) 18 19 if len(d[2]) > 1: # 小于基准值的子数组,递归 20 d[2] = quick_sort(d[2]) 21 22 d[0].extend(d[1]) 23 d[0].extend(d[2]) 24 return d[0] 25 26 27 if __name__ == "__main__": 28 d0 = [2, 15, 5, 9, 7, 6, 4, 12, 5, 4, 2, 64, 5, 6, 4, 2, 3, 54, 45, 4, 44] # 原始乱序 29 d0_out = [2, 2, 2, 3, 4, 4, 4, 4, 5, 5, 5, 6, 6, 7, 9, 12, 15, 44, 45, 54, 64] # 正确排序 30 d1 = quick_sort(d0) 31 print(d1) 32 print(d0_out)
7、堆排序(Heap Sort)【利用最大堆和最小堆的特性】
python代码实现:
1 d0 = [99, 5, 36, 7, 22, 17, 46, 12, 2, 19, 25, 28, 1, 92] 2 3 4 def sort_max(data): # 直接冒泡一下吧,小到大 5 for i in range(len(data) - 1): 6 for j in range(len(data) - 1): 7 if data[j] > data[j + 1]: 8 data[j], data[j + 1] = data[j + 1], data[j] 9 return data 10 11 def heap_min(data,type): 12 index = 0 13 if not type: 14 for i in range(len(data[1:])): 15 if data[index] > data[i+1]: 16 index = i+1 17 data[0],data[index] = data[index],data[0] 18 return data 19 else: 20 for i in range(len(data[1:])): 21 if data[index] < data[i+1]: 22 index = i+1 23 data[0],data[index] = data[index],data[0] 24 return data 25 26 27 # d0 = [3,2,1,10,3] 28 # print(heap_min(d0,1)) 29 # print(heap_min(d0,0)) 30 31 import numpy as np 32 33 34 def heap_adj(data, type): # data 原始堆,type=1最大堆,type=0最小堆 35 length = len(data) 36 floor = int(np.log2(length)) 37 for i in range(floor, 0, -1): # 3(7 6 5 4)-2(3 2)-1(1) 38 for j in range(2 ** floor - 1, 2 ** (floor - i) - 1, -1): 39 # print(i,j) # j-1 为当前父节点 40 d_mid = [data[j - 1]] # j = 7,j-1 =6 index 41 if j * 2 <= length: # 14 42 d_mid.append(data[j * 2 - 1]) 43 if j * 2 + 1 <= length: 44 d_mid.append(data[j * 2]) 45 46 d_mid = heap_min(d_mid, type) 47 48 if len(d_mid) == 2: 49 data[j - 1], data[j * 2 - 1] = d_mid[0], d_mid[1] 50 elif len(d_mid) == 3: 51 data[j - 1], data[j * 2 - 1], data[j * 2] = d_mid[0], d_mid[1], d_mid[2] 52 return data 53 54 d1 = [] 55 for i in range(len(d0)): 56 data = heap_adj(d0, 0) 57 d1.append(d0[0]) 58 del d0[0] 59 60 61 print(d1)
大类二(非比较排序法):
8、计数排序(Counting Sort)【字典计数-还原】
python代码实现:
1 d0 = [2, 15, 5, 9, 7, 6, 4, 12, 5, 4, 2, 64, 5, 6, 4, 2, 3, 54, 45, 4, 44]
2 d0_out = [2, 2, 2, 3, 4, 4, 4, 4, 5, 5, 5, 6, 6, 7, 9, 12, 15, 44, 45, 54, 64]
3
4 d_max = 0
5 d_min = 0
6 for i in d0:
7 if d_max<i:
8 d_max = i
9 if d_min>i:
10 d_min = i
11
12 d1 = {}
13 for i in d0:
14 if i in d1.keys():
15 d1[i] += 1
16 else:
17 d1[i] = 1
18
19 d2 = []
20 for i in range(d_min,d_max+1):
21 if i in d1.keys():
22 for j in range(d1[i]):
23 d2.append(i)
24
25 print(d2)
9、桶排序(Bucket Sort)【链表】
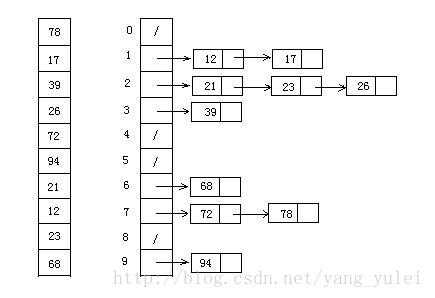
python代码实现:
1 d0 = [2, 15, 5, 9, 7, 6, 4, 12, 5, 4, 2, 64, 5, 6, 4, 2, 3, 54, 45, 4, 44] 2 3 d1 = [[] for x in range(10)] 4 for i in d0: 5 d1[int(i/10)].append(i) 6 7 # print(d1) 8 9 10 for i in range(len(d1)): 11 if d1[i] != []: 12 d2 = [[] for x in range(10)] 13 for j in d1[i]: 14 d2[j%10].append(j) 15 d1[i] = d2 16 17 # print(d1) 18 19 d3 = [] 20 for i in d1: 21 if i: 22 for j in i: 23 if j: 24 for k in j: 25 if k: 26 d3.append(k) 27 print(d3)
10、基数排序(Radix Sort)

python代码实现:
1 d0 = [2, 15, 5, 9, 7, 6, 4, 12, 5, 4, 2, 64, 5, 6, 4, 2, 3, 54, 45, 4, 44] 2 3 d1 = [[] for x in range(10)] 4 5 # 第一次 最小位次排序 6 for i in d0: 7 d1[i % 10].append(i) 8 9 print(d1) 10 11 d0_1 = [] 12 for i in d1: 13 if i: 14 for j in i: 15 d0_1.append(j) 16 print(d0_1) 17 18 # 第二次 次低位排序 19 d2 = [[] for x in range(10)] 20 for i in d0_1: 21 d2[int(i/10)].append(i) 22 print(d2) 23 24 d0_2 = [] 25 for i in d2: 26 if i: 27 for j in i: 28 d0_2.append(j) 29 print(d0_2)
出自 https://www.cnblogs.com/Mufasa/p/10527387.html

