标签：条件   n皇后问题   alt   com   row   n皇后   str   很多   大量   

什么是回溯法？

S：回溯法官网概念是一个类似枚举搜素尝试的过程，是一种选优搜索树，按照某个条件来向前搜索，如果满足条件的时候，就“回溯”，返回到树的上一层，重新试探其他的结果，直到遍历完所有的解空间。个人理解就是该问题的解可以构建一棵解空间树，该题就可以使用回溯法来解决，下面我们使用了N皇后这个经典的问题来解释解空间树和回溯法。

问题实例：N皇后问题

在n×n格的棋盘上放置彼此不受攻击的n个皇后。按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n后问题等价于再n×n的棋盘上放置n个皇后，任何2个皇后不妨在同一行或同一列或同一斜线上。
一下是3皇后问题中的解空间树

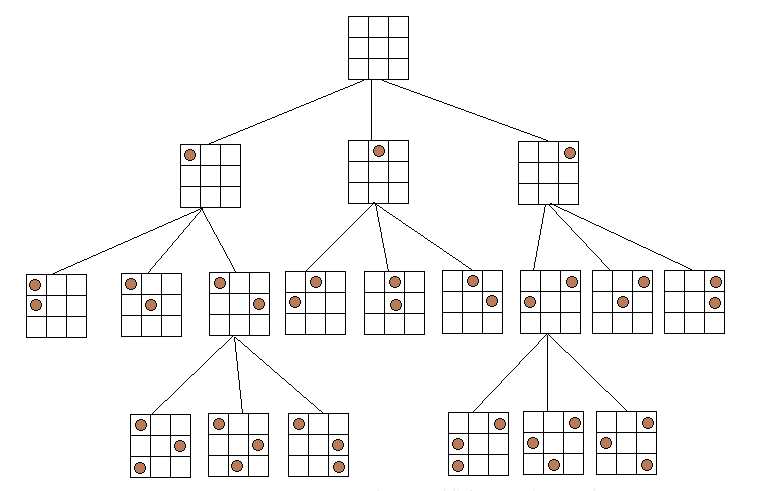
从上面的图示可以看出，3皇后问题的所有的解可以看成上述的一个n叉树问题，因为第一行的棋子有n中可能，对应第一行棋子的一种可能，第二种也有n种可能，如果使用回溯的方法的话，我们需要先将题目的所有解情况先存储起来，然后再对其中的每种情况进行判断是否符合条件，这做需要消耗大量的内存空间；同时在构建的这个解空间的树上，可能还没有走到叶子节点就会发现该情况不行，这样使用回溯法的时候我们就可以直接在该点回溯，也就是向树的上一父节点走，然后遍历父节点的其他情况，这样可以减少空间复杂的同时也减少了时间复杂度。
N皇后问题java代码实现：

package com.leetcode;

import java.util.Queue;

public class NQueens {

    private static final int N = 5;
    static int n = 0;

    /*
    *
    * 八皇后问题：
    * 使用回溯法
    *
    * */

    // Queen（t）摆放第t个皇后

    private static void queen(int t,int[][] bo){
        if(t==N){
            NQueens.n += 1;
            System.out.println("该摆放是可行的"+NQueens.n);
            // 将矩阵结果打印出
            int[] temp = new int[N];
            for (int i = 0; i < N; i++) {
                for (int j = 0; j < N; j++) {
//                    System.out.print(bo[i][j]+"\t");
                    if(bo[i][j] ==1) temp[i] = j+1;
                }
//                System.out.println();
            }
            for (int i = 0; i < temp.length; i++) {
                System.out.print(temp[i]+"\t");
            }
        }
        for (int i = 0; i <N; i++) {
            if (feasible(t,i,bo)){
                bo[t][i] = 1;//可以放置则将棋盘位置置为1
                queen(t+1,bo);
                bo[t][i] = 0;//将摆放的位置恢复
            }

        }
    }

    // factorial 判断（row,col）位置是否可行
    private static boolean feasible(int row,int col,int[][] bo){
        // 输入的位置不合法
        if(row>=N||row<0||col>=N||col<0) return false;
        // 遍历的位置已经有皇后了
        if(bo[row][col]==1) return false;
        // 判断行和列是否有冲突
        for (int i = 0; i < N; i++) {
            if(bo[i][col] == 1 || bo[row][i] ==1) return false;
        }
        //判断斜边是否有冲突，有四个方向需要判断
        for (int i = 0; i < N; i++) {
            //左上
            if(((row-i)>=0 &&(col-i)>=0)&&bo[row-i][col-i]==1) return false;
            // 右上
            if(((row-i)>=0&&(col+i<N))&&bo[row-i][col+i]==1) return false;
            //左下
            if(((row+i<N)&&(col-i>=0))&&bo[row+i][col-i]==1) return false;
            //右下
            if((row+i<N)&&(col+i<N)&&bo[row+i][col+i] == 1) return false;
        }
        return true;
    }

    public static void main(String[] args) {
        // 1.用二维数据来定义棋盘，0代表没有棋子，1代表有棋子
        int[][] board = new int[N][N];
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                board[i][j] = 0;
            }
        }

        queen(0,board);
        System.out.println(N+"皇后共有"+n+"种解法。");
    }
}

实验结果：

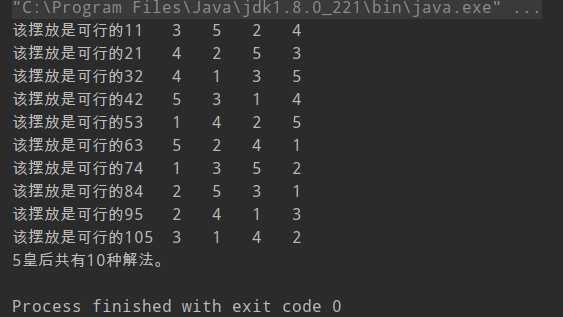
该代码中主要是两个函数：
1.private static boolean feasible(int row,int col,int[][] bo)：该函数用来判断在若棋子在（row，col）放置是否有效，bo是传入的代表棋盘的二维数组，位置有棋子为1，没有为0
2.private static void queen(int t,int[][] bo)：该方法用来放置第t颗棋子，也就是第t行的棋子
程序重点在下图所示位置：

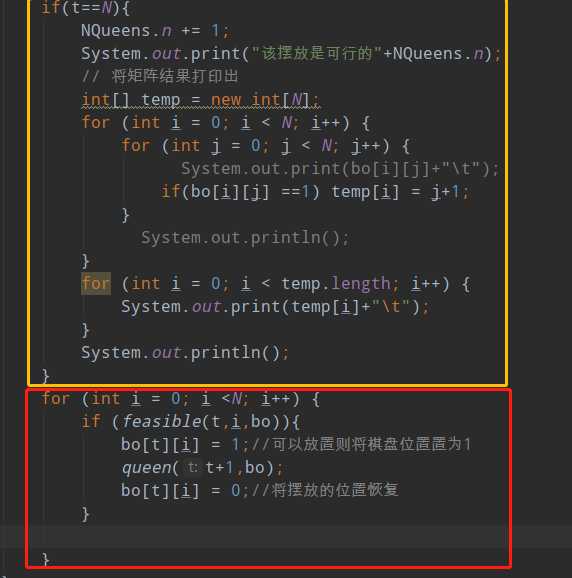
黄框中显示的是当现在放的是第N颗棋子时，表示所有的棋子都已经发现去说明这是一个可行解，我们将结果打印输出
低下的红框中是回溯的过程，若果函数feasible判定为true，则表示该位置可以放，在解空间树里面就是这棵树可以往下走，然后我们使用bo[t][i] = 1将该位置放上棋子，递归使用queen（t+1,b0）就想当时是在解空间树里面向下走了一层，当这一次遍历完之后我们需要返回之前的一层，从解空间树上面可以看出我们需要对棋子归位，这个操作就对应bo[t][i] = 0

改进：：
代码应该还有很多可以改进的地方，以后有时间了再改。

五大算法-1.回溯法

标签：条件   n皇后问题   alt   com   row   n皇后   str   很多   大量   

原文地址：https://www.cnblogs.com/bevishe/p/11901506.html