数据结构与算法(三)--链表

标签：插入   dha   数据结构与算法   就是   时间   失败   访问   处理   动态   

一、链表

• 单项链表、循环链表、双向链表

链表和数组不同，链表的每个元素都存储了下一个元素的地址，所以链表不需要连续的存储空间；

如果我们申请一个 100MB 大小的数组，当内存中没有连续的、足够大的存储空间时，即便内存的剩余总可用空间大于 100MB，仍然会申请失败。

1、单链表：内存块称为链表的“结点”，把这个记录下个结点地址的指针叫作后继指针 next

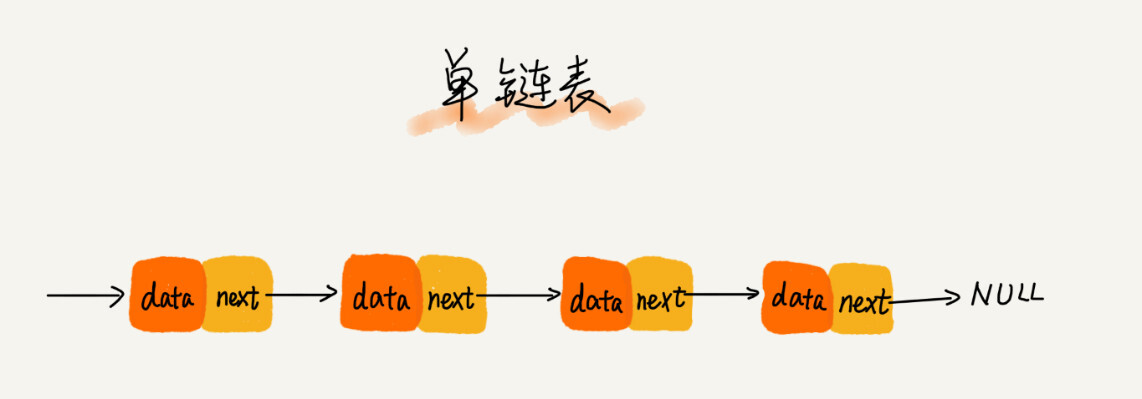
头结点用来记录链表的基地址。有了它，我们就可以遍历得到整条链表。而尾结点特殊的地方是：指针不是指向下一个结点，而是指向一个空地址 NULL，表示这是链表上最后一个结点。

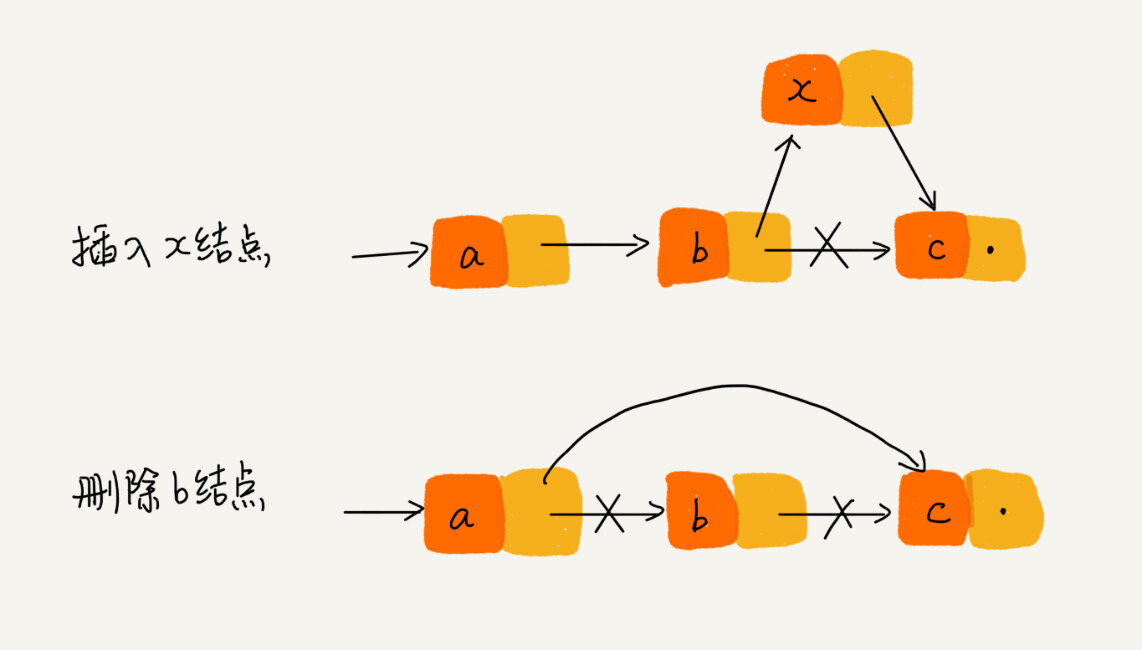
链表的插入和删除操作，我们只需要考虑相邻结点的指针改变，所以对应的时间复杂度是 O(1)

链表随机访问第k个元素，需要根据首地址指针指针一个结点一个结点地依次遍历，直到找到相应的结点，需要 O(n) 的时间复杂度；

2、循环链表：循环链表的是一种特殊的单链表，他的尾节点指向链表的头结点；

循环链表的优点是从链尾到链头比较方便。当要处理的数据具有环型结构特点时，就特别适合采用循环链表。比如著名的约瑟夫问题；

3、双向链表：每个结点不止有一个后继指针 next 指向后面的结点，还有一个前驱指针 prev 指向前面的结点；

从结构上来看，双向链表可以支持 O(1) 时间复杂度的情况下找到前驱结点，正是这样的特点，也使双向链表在某些情况下的插入、删除等操作都要比单链表简单、高效；

实际情况下，单链表与双向链表的元素删除比较：

• 删除结点中“值等于某个给定值”的结点；
• 删除给定指针指向的结点。

1. 第一种情况，不管是单链表还是双向链表，为了查找到值等于给定值的结点，都需要从头结点开始一个一个依次遍历对比，直到找到值等于给定值的结点，然后再通过我前面讲的指针操作将其删除，管单纯的删除操作时间复杂度是 O(1)，但遍历查找的时间是主要的耗时点，对应的时间复杂度为 O(n)。根据时间复杂度分析中的加法法则，删除值等于给定值的结点对应的链表操作的总时间复杂度为 O(n)；

2. 对于第二种情况，我们已经找到了要删除的结点，但是删除某个结点 q 需要知道其前驱结点，而单链表并不支持直接获取前驱结点，所以，为了找到前驱结点，我们还是要从头结点开始遍历链表，直到 p->next=q，说明 p 是 q 的前驱结点;

   而双向链表可以直接获取到节点的前驱结点，对元素进行删除操作，

   单链表删除操作需要 O(n) 的时间复杂度，而双向链表只需要在 O(1) 的时间复杂度

   LinkedHashMap 的实现原理，就会发现其中就用到了双向链表这种数据结构

3. 双向循环链表：是双向链表和循环链表的结合：

   

链表 VS 数组性能 比较

• 数组简单易用，在实现上使用的是连续的内存空间，可以借助 CPU 的缓存机制，预读数组中的数据，所以访问效率更高。而链表在内存中并不是连续存储，所以对 CPU 缓存不友好，没办法有效预读。
• 数组的缺点是大小固定，一经声明就要占用整块连续内存空间。如果声明的数组过大，系统可能没有足够的连续内存空间分配给它，导致“内存不足（out of memory）”。如果声明的数组过小，则可能出现不够用的情况。这时只能再申请一个更大的内存空间，把原数组拷贝进去，非常费时。链表本身没有大小的限制，天然地支持动态扩容。
• 如果你的代码对内存的使用非常苛刻，那数组就更适合你。因为链表中的每个结点都需要消耗额外的存储空间去存储一份指向下一个结点的指针，所以内存消耗会翻倍。而且，对链表进行频繁的插入、删除操作，还会导致频繁的内存申请和释放，容易造成内存碎片，如果是 Java 语言，就有可能会导致频繁的 GC（Garbage Collection，垃圾回收；

二、基于链表实现 LRU 缓存淘汰算法？

我们维护一个有序单链表，越靠近链表尾部的结点是越早之前访问的。当有一个新的数据被访问时，我们从链表头开始顺序遍历链表。

1. 如果此数据之前已经被缓存在链表中了，我们遍历得到这个数据对应的结点，并将其从原来的位置删除，然后再插入到链表的头部。
2. 如果此数据没有在缓存链表中，又可以分为两种情况：
   • 如果此时缓存未满，则将此结点直接插入到链表的头部；
   • 如果此时缓存已满，则链表尾结点删除，将新的数据结点插入链表的头部。

因为不管缓存有没有满，我们都需要遍历一遍链表，所以这种基于链表的实现思路，缓存访问的时间复杂度为 O(n)。

三、链表的实现

• 想要写好链表代码并不是容易的事儿，尤其是那些复杂的链表操作，比如链表反转、有序链表合并等，写的时候非常容易出错。从我上百场面试的经验来看，能把“链表反转”这几行代码写对的人不足 10%。

链表的实现技巧

1. 技巧一：理解指针或引用的含义
   • 将某个变量赋值给指针，实际上就是将这个变量的地址赋值给指针，或者反过来说，指针中存储了这个变量的内存地址，指向了这个变量，通过指针就能找到这个变量。
     • 在编写链表代码的时候，我们经常会有这样的代码：p->next=q。这行代码是说，p 结点中的 next 指针存储了 q 结点的内存地址。
     • 还有一个更复杂的，也是我们写链表代码经常会用到的：p->next=p->next->next。这行代码表示，p 结点的 next 指针存储了 p 结点的下下一个结点的内存地址。

2. 技巧二：警惕指针丢失和内存泄漏

   

   错误代码：

   p->next = x;  // 将p的next指针指向x结点；
   x->next = p->next;  // 将x的结点的next指针指向b结点；

   第二行的代码中，此时p->next已经是x的地址了，x->next = x，正确的代码是交换两行底代码的顺序；

3. 技巧三：利用哨兵简化实现难度

?

数据结构与算法(三)--链表

标签：插入   dha   数据结构与算法   就是   时间   失败   访问   处理   动态   

原文地址：https://www.cnblogs.com/liweiweicode/p/11959379.html