标签：执行   处理   ==   string   cst   return   std   图片   memset   

暴力

其实这题的暴力就是个模拟。暴力扫一遍 \(conn(s_1, n_1)\)，若出现了 \(res\) 个 \(s_2\)。

答案就是 \(\lfloor res / n1 \rfloor\)。

时间复杂度 \(O(T(|s_1|n1))\)。

优化

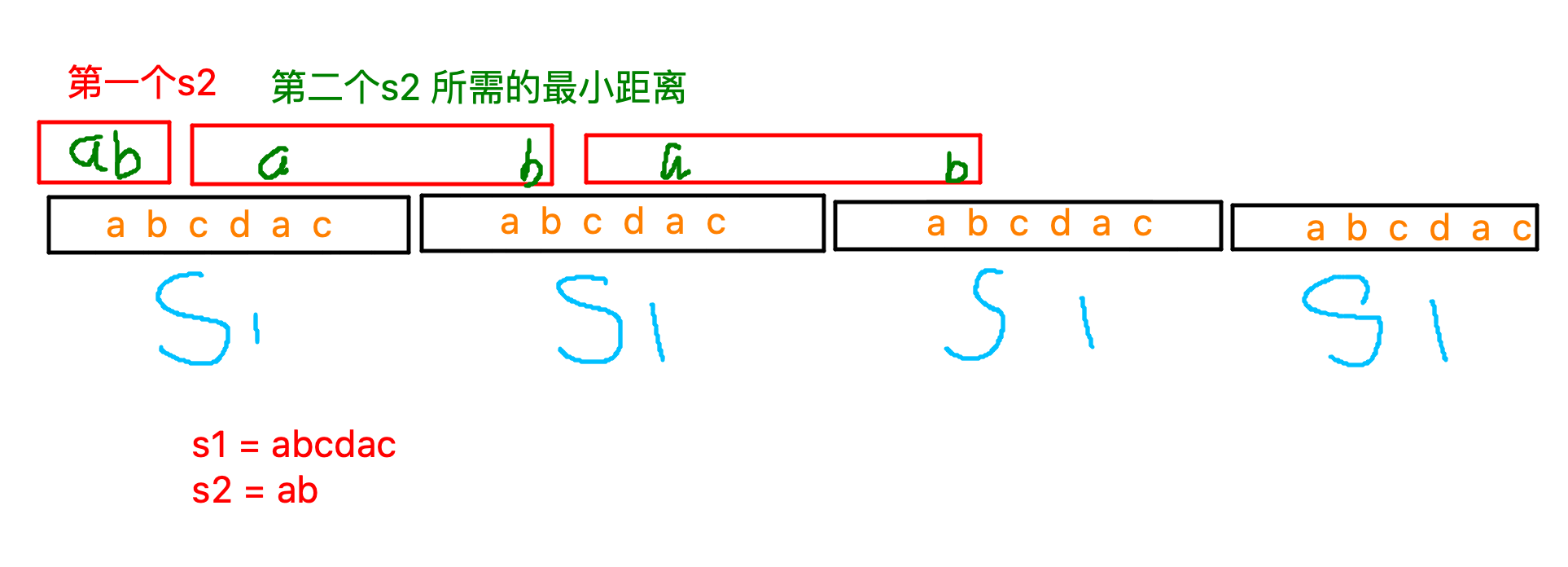
考虑字符串是一直循环的，每走完一个 \(s_2\)，他会从一个位置重新开始匹配。我们考虑预处理出对于从 \(0\) ~ \(|s1|- 1\) 这个下标 \(i\) 开始，匹配一个 \(s_2\) 所需最小的字符数，设其为 \(f[i]\)。

那么我们就不需要把整个 \(conn(s_1, n_1)\) 搞出来了，可以搞一个变量 \(p = 0\) 表示当前走过的字符数，设出现的 \(s2\) 个数 \(res = 0\)，循环执行：

如果 \(p + f[p \% |s1|] <= n1 *|s1|\)，就 \(p += f[p \% |s1|], ans++\)。形象理解就是如果还能匹配一个 \(s2\)，并且不超过限制，我就再过一个 \(s_2\)，知道上述条件不符合时停止。

考虑最坏时答案是 \(|s_1| * n1 / |s2|\)。

所以 时间复杂度 \(O(T(|s_1| * n1 / |s2|))\)。最坏情况下和暴力一样的，想了那么久你 tm 跟暴力还一样。。

倍增

刚才的跳的过程可以描述为：

• 能跳就跳
• 对于每个 \(p\) ，有唯一的后继 \(p + f[p \% |s1|]\)

这不就是明显的可以倍增优化吗？

设 \(dp[i][j]\) 为\(s_1\)循环节从下标 \(i\) 出发，匹配 \(2 ^ j\) 个 \(s_2\) 串所需的最小字符数。

初始状态：\(dp[i][0] = f[i]\)

状态转移：\(dp[i][j] = dp[i][j - 1] + dp[(i + dp[i][j - 1]) \% |s1|][j - 1]\)，就是用两个 \(2 ^{j - 1}\) 拼出 \(2 ^ j\)。

跳的时候就用倍增模板就行了：

初始设 \(p = 0, res = 0\)，从大到小枚举 \(j\)：

• 如果 \(p + f[p \% |s1|][j] <= n1 *|s1|\)，就 \(p += f[p \% |s1|][j], ans += 2 ^ j\)。

\(Tips：\)此题输入比较毒瘤，建议用 \(cin\)。因为如果用 \(scanf\) 貌似最后有个换行如果用 \(\not= EOF\) 会再算一组数据...

时间复杂度

\(O(T(n ^ 3 + nlog_{|s_1| * n1 / |s2|}))\)。大概最坏情况 \(O(1000000T)\) 左右。

#include <cstdio>
#include <iostream>
#include <cstring>
#include <cmath>
using namespace std;
const int N = 105;
char s1[N], s2[N];
int n1, n2, len1, len2, L, f[N][27];
int main() {
    while(scanf("%s %d\n%s %d", s2, &n2, s1, &n1) == 4) {
        memset(f, 0, sizeof f);
        len1 = strlen(s1), len2 = strlen(s2), L = log2(len1 * n1 / len2);
        for (int i = 0; i < len1; i++)
            for (int j = 0; f[i][0] <= len1 * len2 && j < len2; f[i][0]++) 
                if(s2[j] == s1[(i + f[i][0]) % len1]) j++;
        if (f[0][0] > len1 * len2) { puts("0"); continue; }
        for (int j = 1; j <= L; j++)
            for (int i = 0; i < len1; i++)
                f[i][j] = f[i][j - 1] + f[(i + f[i][j - 1]) % len1][j - 1];
        int p = 0, ans = 0;
        for (int i = L; i >= 0; i--) 
            if(p + f[p % len1][i] <= len1 * n1) p += f[p % len1][i], ans += 1 << i;
        printf("%d\n", ans / n2);
    }
    return 0;
}

AcWing 294. 计算重复

标签：执行   处理   ==   string   cst   return   std   图片   memset   

原文地址：https://www.cnblogs.com/dmoransky/p/11960657.html