标签:一半 mes 如何 好的 iostream img 相等 根据 main
快速排序为什么被称之为快速排序呢?从字面意思上来看肯定是因为它比较快啦。当然实际上也是这样,相比于其他的排序算法,它的平均的时间复杂度为O(nlogn),这可以说是很快的一种排序算法了。当然在某些情况下,也会出现比其他排序算法慢的情形,所以没有什么最好的排序算法,只有最合适的排序算法。所以在平常应用的时候要根据实际情况来选择合适的排序算法。
拿为什么快排比较快呢?因为它每次进行了划分,选择一个基准值后,将这个待排序序列分成了小于基准值的一半和大于基准值的一半,然后继续进行相同的操作,知道最后的一半只剩下一个元素。
1.分解:数组A[p...r]被划分为连个子数组A[p...q-1]和A[q+1...r],使得A[p...q-1]中所有的数都比A[q]小,A[q+1...r]中所有的数都比A[q]大;
2.解决:通过递归调用快速排序,对子数组A[p...q-1]和A[q+1...r]进行排序;
3.合并:因为数组原址排序,所进行完之后数组A[p...r]已经有序。
代码如下:
1 quicksort(int a[],int l,int r){//快排递归形式 2 if(l<r){ 3 int q=partition(a,l,r);//找到中间数,不一定是中位数 4 quicksort(a,l,q-1); 5 quicksort(a,q+1,r); 6 } 7 }
所以接下就是如何解决划分(partition)的问题了。有三种方法可以来解决划分的问题:一遍单向扫描法,双向扫描法和三分法,接下来我们就来好好看看这三种方法。
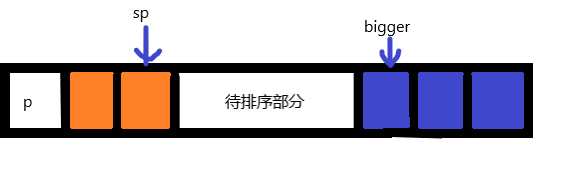
思路:首先找到一个基准值p,使用两个指针(sp,bigger)将待排序的数组分成三个部分,sp左边的表示全部小于基准值的,bigger右边的部分表示全部大于基准值的,sp和bigger之间的部分为待排序的部分。
当sp元素小于p时,交换sp和bigger的元素,然后bigger--。
代码如下:
1 int partition(int a[],int l,int r){ 2 int x=a[l];//基准值 3 int sp=l+1,bigger=r;//选定两个指针 4 while(sp<=bigger){ 5 if(a[sp]<=x) ++sp;//当扫面元素小于基准值时,右移扫描指针 6 else {//当扫描元素大于基准值时,两个指针的元素交换,然后左移右侧指针 7 swap(a[sp],a[bigger]); 8 --bigger; 9 } 10 } 11 swap(a[l],a[bigger]);//最后基准值与bigger指针元素交换,得到 12 return bigger;//得到中间值 13 }
一遍单向扫描只能从一个放向走到底,这样看起来是不是也很慢呢?如果我们让这两个指针进行相对的移动是不是更快了!!这就是我们接下来要介绍的双向扫描法。
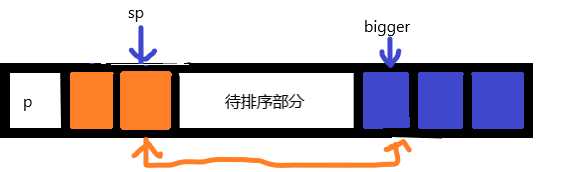
思路:和上面的一遍单向扫描法一样也是设置两个指针分别为左指针sp,右指针bigger,最终得到的结果也是sp左边的元素都比p小,bigger右边的元素都比p大。那和一遍单向扫描法的区别在于sp和bigger指针同时相向移动,当sp元素大于p且bigger元素大于p时,两个指针所指的元素交换位置,然后继续移动指针,直到到达边界条件。
代码如下:
1 int partition(int a[],int l,int r){ 2 int x=a[l];//基准值 3 int p=l+1,q=r; 4 while(p<=q){ 5 //记住得加上边界条件,因为在移动指针的过程中可能会越界 6 while(a[p]<=x&&p<=q) ++p;//sp元素小于p则右移 7 while(a[q]>x&&p<=q) --q;//bigger元素大于p则左移 8 if(p<=q) swap(a[p],a[q]);//交换两指针元素 9 } 10 //此时bigger在sp左边且bigger所指元素是小于p的 11 swap(a[l],a[q]);//最后还得与基准值交换 12 return q; 13 }
最后还有一种较为特殊的情况,当待排序序列中的重复元素较多时,我们可以使用一个equal指针来指向与基准值相等的元素,然后返回相等序列的头部和尾部。接下来我们就介绍下这个方法。
思路:1.选定基准值,
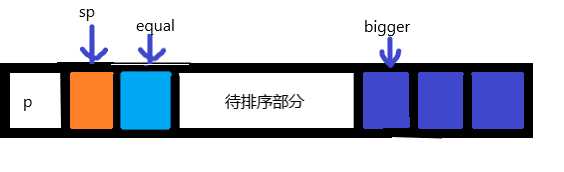
2.使用三个指针,一个扫描指针sp,一个右指针bigger,一个相等指针equel
3.当sp小于基准值时,equel元素与sp元素交换,然后equel,sp右移,
当sp等于基准值时,sp右移
当sp元素大于基准值时,sp元素与bigger元素交换,bigger左移
4.最后equel-1元素与基准值交换,返回equel-1和bigger
代码如下:
1 #include<iostream> 2 #include<algorithm> 3 using namespace std; 4 5 struct equal {//使用一个结构体来存储中间相等区间的左边界和右边界 6 int right; 7 int left; 8 }equal1; 9 10 void partition(int a[],int l,int r){ 11 int x=a[l]; 12 int sp=l+1,e=l+1,bigger=r; 13 while(sp<=bigger){ 14 if(a[sp]<x) { 15 swap(a[e],a[sp]); 16 ++e; 17 ++sp; 18 } 19 else if(a[sp]==x) ++sp; 20 else { 21 swap(a[bigger],a[sp]); 22 --bigger; 23 } 24 } 25 swap(a[l],a[e-1]); 26 equal1.right=bigger; 27 equal1.left=e-1; 28 } 29 30 quicksort(int a[],int l,int r){//快排递归形式 31 if(l<r){ 32 partition(a,l,r);//找到中间数,不一定是中位数 33 quicksort(a,l,equal1.left-1); 34 quicksort(a,equal1.right+1,r); 35 } 36 } 37 int main(){ 38 int a[10]={4,6,4,2,8,0,1,4,5,4};//测试数据 39 quicksort(a,0,9); 40 for(int i=0;i<10;i++) cout<<a[i]<<" "; 41 cout<<endl; 42 return 0; 43 }
以上就是快排的三种基本方法,可以根据实际情况来选择使用哪中划分方法。欢迎大家指正哦~,如果喜欢的话,点个关注呗(●‘?‘●)。
标签:一半 mes 如何 好的 iostream img 相等 根据 main
原文地址:https://www.cnblogs.com/algorithm-process/p/11963856.html