标签:次数 分配 shape 大于 plot 较差 sts 类别 info
聚类算法是常见的无监督学习(无监督学习是在样本的标签未知的情况下,根据样本的内在规律对样本进行分类)。
在监督学习中我们常根据模型的误差来衡量模型的好坏,通过优化损失函数来改善模型。而在聚类算法中是怎么来度量模型的好坏呢?聚类算法模型的性能度量大致有两类:
1)将模型结果与某个参考模型(或者称为外部指标)进行对比,个人觉得认为这种方法用的比较少
2)另一种是直接使用模型的内部属性,比如样本之间的距离(闵可夫斯基距离)来作为评判指标,这类称为内部指标。
其中内部指标如下:

公式解释如下:
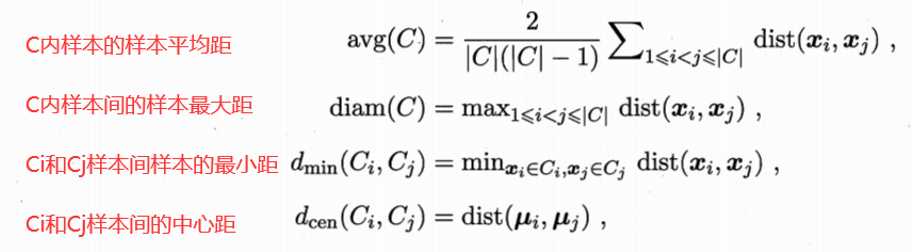
距离定义
K-means算法是聚类算法的一种,实现起来比较简单,效果也不错。K-means的思想很简单,对于给定的样本集,根据样本之间距离的大小将样本划分为K个簇(在这里K是需要预先设定好的)
思路:在进行划分簇时要尽量让簇内的样本之间的距离很小,让簇与簇之间的距离尽量大。
在给定的数据集D的条件下,将数据集划分为K类,则K-means的数学模型可以表示:
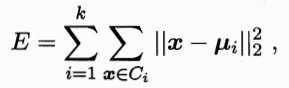
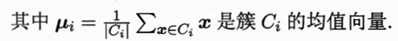
其中Ci为第i类的集合,μi为第i类的簇心(该簇内所有样本的均值,也称为均值向量)

(数据来源 机器学习-周志华版)
主要核心有两步:
K-Means采用的启发式方式很简单,下图就可以形象的描述过程:
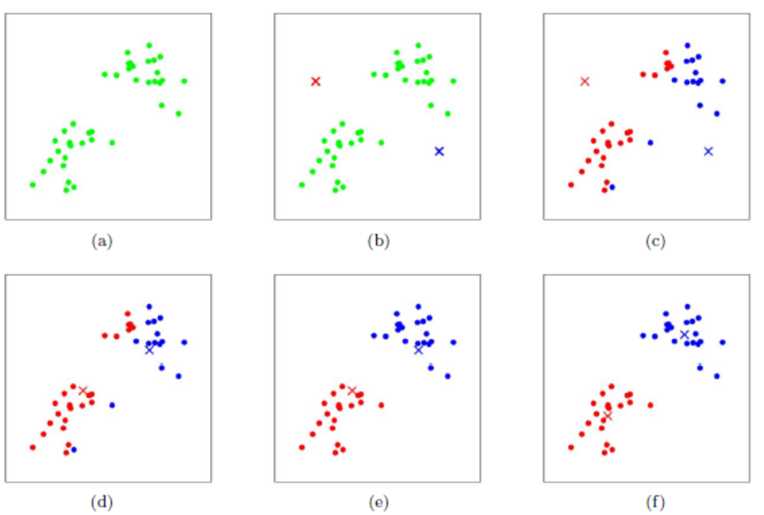
1)在初始化时,随机选择K个样本作为初始的簇心,倘若此时随机的结果不好,比如两个随机的簇心挨得很近,这可能会导致模型收敛的速度减慢,常见的解决方式:K-Means++的优化。
2)每次迭代时都要计算所有样本和所有簇心之间的距离,若此时样本很大,或者簇心很多时,计算代价是非常大的。
方法一:Mini Batch K-Means--因此每次随机抽取一小批样本来更新当前的簇心(通过无放回随机采样);
方法二: elkan K-Means)--利用了两边之和大于等于第三边,以及两边之差小于第三边的三角形性质,来减少距离的计算。
1)原理简单,实现容易,且收敛速度也较快。
2)聚类效果较好,而且可解释性较强。
3)参数很少,需要调的参数只有簇的个数K。
1)K值的选取比较难
2)对于非凸数据集收敛比较难
3)如果隐含类别的数据不平衡,则聚类效果不佳,比如隐含类型的方差不同,方差较大的类中的样本可能会被聚类到其他类别中,在聚类时原则上没啥影响,但是聚类或者说无监督学习大多时候都是一些预训练,聚类后的数据可能之后会被用于其他的分类回归模型中
4)对噪声和异常点比较敏感
5)迭代得到的结果只是局部最优
k-medoids 和 k-means 不一样的地方在于中心点的选取,在 k-means 中,我们将中心点取为当前 cluster 中所有数据点的平均值。并且我们已经证明在固定了各个数据点的 assignment 的情况下,这样选取的中心点能够把目标函数 J 最小化。然而在 k-medoids 中,我们将中心点的选取限制在当前 cluster 所包含的数据点的集合中。换句话说,在 k-medoids 算法中,我们将从当前 cluster 中选取这样一个点——它到其他所有(当前 cluster 中的)点的距离之和最小——作为中心点。k-means 和 k-medoids 之间的差异就类似于一个数据样本的均值 (mean) 和中位数 (median) 之间的差异:前者的取值范围可以是连续空间中的任意值,而后者只能在给样本给定的那些点里面选。
DBSCAN(Density-Based Spatial Clustering of Applications with Noise,具有噪声的基于密度的聚类方法)是一种很典型的密度聚类算法,和K-Means,BIRCH这些一般只适用于凸样本集的聚类相比,DBSCAN既可以适用于凸样本集,也可以适用于非凸样本集。
同一类别的样本,他们之间是紧密相连的,通过样本密度来考察样本之间的可连接性,并基于可连接样本不断扩展聚类簇以获得最终的聚类结果。因此密度聚类也是不需要提前设置簇数K的值的。DBSCAN是基于一组领域来描述样本集的紧密程度的。
不太恰当的比喻:类似传销,画圈找点发展下线,比较适合做检测,找到离散点
给定数据集D{x1, x2, ......xn}
1)?- 邻域:对于xi ,其邻域中包含了所有与xi 的距离小于? 的样本
2)核心对象:对于任一样本xj∈D,如果其?-邻域对应的N???(xj)至少包含MinPts个样本,即如果|N???(xj)|?≥?MinPts,则xj是核心对象
3)密度直达:如果xi?位于xj?的?-邻域中,且xj?是核心对象。
4)密度可达:对于xi和xj,如果存在样本样本序列p1,?p2,...,?pT,满足p1=xi,pT=xj,且pt+1由pt?密度直达,则称xj?由xi?密度可达。也就是说,密度可达满足传递性。此时序列中的传递样本p1,p2,...,pT?1均为核心对象,因为只有核心对象才能使其他样本密度直达。注意密度可达也不满足对称性,这个可以由密度直达的不对称性得出
5)密度相连:对于xi和xj,如果存在核心对象样本xk,使xi和xj均由xk密度可达,则称xi和xj密度相连。注意密度相连关系是满足对称性的.
? ?
如下图所示,对于给定的MinPts=3,x1是核心对象,x2由x1密度直达,x3由x1密度可达,x3由x4密度相连。
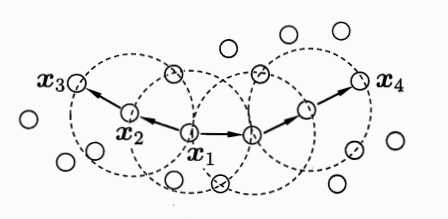
有密度可达关系导出的最大的密度相连样本集合。即分类簇C必须满足:
1)连接性:xi∈ C,可以直接推出xi?与xj?密度相连,同簇内的元素必须满足密度相连
2)最大性:xi∈ C,xj?有xi?密度可达可以推出xj?∈C?

数据来源 机器学习-周志华版
1)根据预先给定的(?,MinPts)确定核心对象的集合
2)从核心对象集合中任选一核心对象,找出由其密度可达的对象生成聚类簇
3)从核心对象中除掉已选的核心对象和已分配到簇中的核心对象(这说明在一个簇内肯能存在多个核心对象)
4)重复2,3 步骤,直到所有的核心对象被用完
DBSACN算法理解起来还是比较简单的,但是也存在一些问题:
1)在所有的核心对象都被用完之后,可能还是会存在一些样本点没有被分配到任何簇中,此时我们认为这些样本点是异常点
2)对于有的样本可能会属于多个核心对象,而且这些核心对象不是密度直达的,那么在我们的算法中事实上是采用了先来先到的原则
与K-means算法相比,DBSCAN算法有两大特点
一是不需要预先设定簇数K的值
二是DBSCAN算法同时适用于凸集和非凸集,而K-means只适用于凸集,在非凸集上可能无法收敛。对于DBSCAN算法适用于稠密的数据或者是非凸集的数据,此时DBSCAB算法的效果要比K-means算法好很多。因此若数据不是稠密的,我们一般不用DBSCAN算法。
1)可以对任意形状的稠密数据进行聚类(包括非凸集)
2)可以在聚类是发现异常点,对异常点不敏感
3)聚类结果比较稳定,不会有什么偏倚,而K-means中初始值对结果有很大的影响
1)样本集密度不均匀时,聚类间距相差很大时,聚类效果不佳
2)样本集较大时,收敛时间长,可以用KD树进行最近邻的搜索
3)需要调试的参数比K-means多些,需要去调试? 和MinPts参数(联合调参,不同的组合的结果都不一样)
层次(Hierarchical methods)聚类试图在不同的层次上对数据集进行划分,从而形成树形的聚类结构,数据集的划分可采用 "自底向上"的聚类策略,也可以采用" 自顶向下" 的策略。在构建树之后,所有的样本都位于叶节点中,叶节点的个数就是簇数。AGNES是一种采用自底向上的聚类策略的层次聚类算法。
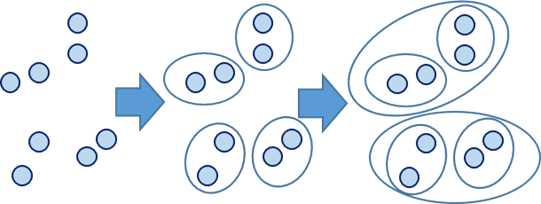
这种方法的好处是随着簇类数量的减少,需要计算的距离也会越来越少,而且相对K-means,不需要考虑初始化时随机簇心对模型到来的影响。在这里主要有三种计算策略:
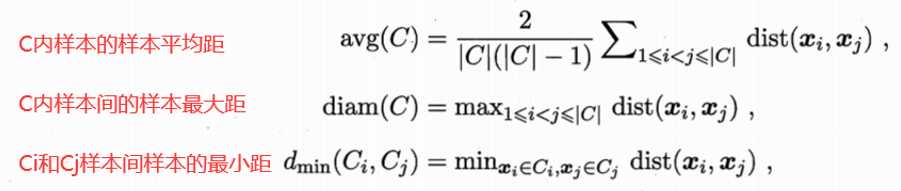
(1) 将每个对象看作一类,计算两两之间的最小距离;
(2) 将距离最小的两个类合并成一个新类;
(3) 重新计算新类与所有类之间的距离;
(4) 重复(2)、(3),直到所有类最后合并成一类。

数据来源 机器学习-周志华版
1,距离和规则的相似度容易定义,限制少;
2,不需要预先制定聚类数;
3,可以发现类的层次关系;
4,可以聚类成其它形状
1,计算复杂度太高;
2,奇异值也能产生很大影响;
3,算法很可能聚类成链状
? ?
关于层次聚类,除了AGNES算法之外,还有BIRCH算法,BIRCH算法适用于数据量大,簇类K的数量较多的情况下,这种算法只需要遍历一遍数据集既可以完成聚类,运行速度很快。BIRCH算法利用了一个类似于B+树的树结构来帮助我们快速聚类,一般我们将它称为聚类特征数(简称CF Tree),BIRCH算法属于自上向下的层次聚类算法(根据数据集的导入自上而下不断的分裂加层来构建CF 树),CF 树中的每个叶节点就对应着一个簇。因此BIRCH算法事实上就是在构建一颗树,构建完之后,树的叶节点就是对应的簇,叶节点中的样本就是每个簇内的样本。BIRCH适用于大样本集,收敛速度快,且不需要设定簇数K的值,但是要设定树的结构约束值(比如叶节点中样本的个数,内节点中样本的个数),此外BIRCH算法对于数据特征维度很大的样本(比如大于20维)不适合。
? ?
k-Means | K-Medoids |
初始据点随机选取 | 初始随机据点限定在样本点中 |
取出同一类别的所有样本,求每一列的平均值,得到新的中心向量, 使用Means(均值)作为聚点,对outliers(极值)很敏感. | 遍历中心样本,该中心样本划分出来的该簇样本,遍历该簇样本,找出离所有样本距离最小的样本,代替旧中心。使用Medoids(中位数)作为聚点。 |
中心点不一定是序列上的点 | 中心点一定在序列类,并且距离各点最小 |
对数据要求高,要求数据点处于欧式空间中 | 可适用类别(categorical)类型的特征 |
时间复杂度:O(n*k*t),t为迭代次数 | 时间复杂度:O(n^2 *k*t),t为迭代次数 |
?K-Means 算法对小规模数据集较高效(efficient? for? smaller? data? sets) | K-Medoids算法对大规模数据性能更好,但伸缩性较差 |
相同点 | |
都有可能陷入局部最优解的困境之中 | |
K的含义相同,都需要开始人为设定簇数目 | |
都是无监督算法 |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 | # Author:yifan #K-means from numpy import * import time import matplotlib.pyplot as plt import numpy as np ? ? # euclDistance函数计算两个向量之间的欧氏距离 def euclDistance(vector1, vector2): return sqrt(sum(power(vector2 - vector1, 2))) # initCentroids选取任意数据集中任意样本点作为初始均值点 # dataSet: 数据集, k: 人为设定的聚类簇数目 # centroids: 随机选取的初始均值点 def initCentroids(dataSet, k): numSamples, dim = dataSet.shape centroids = zeros((k, dim)) #k行dim的0矩阵 for i in range(k): index = int(random.uniform(0, numSamples)) #从0到numSamples中随机选取一个数字 centroids[i, :] = dataSet[index, :] #随机选出k个数字,即为本函数的目的 # print(centroids) return centroids ? ? # kmeans: k-means聚类功能主函数 # 输入:dataSet-数据集,k-人为设定的聚类簇数目 # 输出:centroids-k个聚类簇的均值点,clusterAssment-聚类簇中的数据点 def kmeans(dataSet, k): numSamples = dataSet.shape[0] clusterAssment = mat(zeros((numSamples, 2))) # clusterAssment第一列存储当前点所在的簇 # clusterAssment第二列存储点与质心点的距离 clusterChanged = True #用于遍历的标记 ## 步骤一: 初始化均值点 centroids = initCentroids(dataSet, k) while clusterChanged: clusterChanged = False ## 遍历每一个样本点 for i in range(numSamples): minDist = 100000.0 # minDist:最近距离,初始定一个较大的值 minIndex = 0 # minIndex:最近的均值点编号 ## 步骤二: 寻找最近的均值点 for j in range(k): distance = euclDistance(centroids[j, :], dataSet[i, :]) #每个点和中心点的距离,共有k个值 if distance < minDist: #循环去找最小的那个 minDist = distance minIndex = j ## 步骤三: 更新所属簇 if clusterAssment[i, 0] != minIndex: clusterChanged = True clusterAssment[i, :] = minIndex, minDist**2 #记录序号和点与质心点的距离 ## 步骤四: 更新簇的均值点 for j in range(k): pointsInCluster = dataSet[nonzero(clusterAssment[:, 0] == j)[0]] #当前属于j类的序号 print(pointsInCluster) print(‘ddddd‘) # print(clusterAssment[:, 0]) centroids[j, :] = mean(pointsInCluster, axis = 0) #按照 列计算均值 print (‘Congratulations, cluster complete!‘) return centroids, clusterAssment ? ? # showCluster利用pyplot绘图显示聚类结果(二维平面) # 输入:dataSet-数据集,k-聚类簇数目,centroids-聚类簇的均值点,clusterAssment-聚类簇中数据点 def showCluster(dataSet, k, centroids, clusterAssment): numSamples, dim = dataSet.shape if dim != 2: print ("Sorry, the dimension of your data is not 2!") return 1 mark = [‘or‘, ‘ob‘, ‘og‘, ‘ok‘, ‘^r‘, ‘+r‘, ‘sr‘, ‘dr‘, ‘<r‘, ‘pr‘] if k > len(mark): return 1 # 画出所有的样本点 for i in range(numSamples): markIndex = int(clusterAssment[i, 0]) plt.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex]) mark = [‘Dr‘, ‘Db‘, ‘Dg‘, ‘Dk‘, ‘^b‘, ‘+b‘, ‘sb‘, ‘db‘, ‘<b‘, ‘pb‘] # 标记簇的质心 for i in range(k): plt.plot(centroids[i, 0], centroids[i, 1], mark[i], markersize = 12) plt.show() ? ? ? ? ## step 1: 构造数据 matrix1=np.random.random((12,2)) matrix2=np.random.random((12,2)) matrix3=np.random.random((12,2)) matrix4=np.random.random((12,2)) for i in range(12): matrix2[i,0] = matrix2[i,0]+2 matrix3[i,1] = matrix3[i,1]+2 matrix4[i,:] = matrix4[i,:]+2 dataSet = np.vstack((matrix1,matrix2,matrix3,matrix4)) # print(dataSet) ## step 2: 开始聚类... # dataSet = mat(dataSet) k = 4 centroids, clusterAssment = kmeans(dataSet, k) ## step 3: 显示聚类结果 showCluster(dataSet, k, centroids, clusterAssment) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 | # Author:yifan from numpy import * import time import matplotlib.pyplot as plt import numpy as np ? ? # euclDistance函数计算两个向量之间的欧氏距离 def euclDistance(vector1, vector2): return sqrt(sum(power(vector2 - vector1, 2))) # initCentroids选取任意数据集中任意样本点作为初始均值点 # dataSet: 数据集, k: 人为设定的聚类簇数目 # centroids: 随机选取的初始均值点 def initCentroids(dataSet, k): numSamples, dim = dataSet.shape centroids = zeros((k, dim)) #k行dim的0矩阵 for i in range(k): index = int(random.uniform(0, numSamples)) #从0到numSamples中随机选取一个数字 centroids[i, :] = dataSet[index, :] #随机选出k个数字,即为本函数的目的 # print(centroids) return centroids #定义每个点到其他点的距离和。步骤四的更新簇的均值点时会用到 def costsum( vector1,matrix1): sum = 0 for i in range(matrix1.shape[0]): sum += euclDistance(matrix1[i,:], vector1) return sum # kmediod: k-mediod聚类功能主函数 # 输入:dataSet-数据集,k-人为设定的聚类簇数目 # 输出:centroids-k个聚类簇的均值点,clusterAssment-聚类簇中的数据点 def kmediod(dataSet, k): numSamples = dataSet.shape[0] clusterAssment = mat(zeros((numSamples, 2))) # clusterAssment第一列存储当前点所在的簇 # clusterAssment第二列存储点与质心点的距离 clusterChanged = True #用于遍历的标记 ## 步骤一: 初始化均值点 centroids = initCentroids(dataSet, k) while clusterChanged: clusterChanged = False ## 遍历每一个样本点 for i in range(numSamples): minDist = 100000.0 # minDist:最近距离,初始定一个较大的值 minIndex = 0 # minIndex:最近的均值点编号 ## 步骤二: 寻找最近的均值点 for j in range(k): distance = euclDistance(centroids[j, :], dataSet[i, :]) #每个点和中心点的距离,共有k个值 if distance < minDist: #循环去找最小的那个 minDist = distance minIndex = j ## 步骤三: 更新所属簇 if clusterAssment[i, 0] != minIndex: clusterChanged = True clusterAssment[i, :] = minIndex, minDist**2 #记录序号和点与质心点的距离 ## 步骤四: 更新簇核心点 for j in range(k): pointsInCluster = dataSet[nonzero(clusterAssment[:, 0] == j)[0]] #当前属于j类的序号 mincostsum = costsum(centroids[j,:],pointsInCluster) for point in range(pointsInCluster.shape[0]): cost = costsum( pointsInCluster[point, :],pointsInCluster) if cost < mincostsum: mincostsum = cost centroids[j, :] = pointsInCluster[point, :] print (‘Congratulations, cluster complete!‘) return centroids, clusterAssment ? ? # showCluster利用pyplot绘图显示聚类结果(二维平面) # 输入:dataSet-数据集,k-聚类簇数目,centroids-聚类簇的均值点,clusterAssment-聚类簇中数据点 def showCluster(dataSet, k, centroids, clusterAssment): numSamples, dim = dataSet.shape if dim != 2: print ("Sorry, the dimension of your data is not 2!") return 1 mark = [‘or‘, ‘ob‘, ‘og‘, ‘ok‘, ‘^r‘, ‘+r‘, ‘sr‘, ‘dr‘, ‘<r‘, ‘pr‘] if k > len(mark): return 1 # 画出所有的样本点 for i in range(numSamples): markIndex = int(clusterAssment[i, 0]) plt.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex]) mark = [‘Dr‘, ‘Db‘, ‘Dg‘, ‘Dk‘, ‘^b‘, ‘+b‘, ‘sb‘, ‘db‘, ‘<b‘, ‘pb‘] # 标记簇的质心 for i in range(k): plt.plot(centroids[i, 0], centroids[i, 1], mark[i], markersize = 12) plt.show() ? ? ? ? ## step 1: 构造数据 matrix1=np.random.random((12,2)) matrix2=np.random.random((12,2)) matrix3=np.random.random((12,2)) matrix4=np.random.random((12,2)) for i in range(12): matrix2[i,0] = matrix2[i,0]+2 matrix3[i,1] = matrix3[i,1]+2 matrix4[i,:] = matrix4[i,:]+2 dataSet = np.vstack((matrix1,matrix2,matrix3,matrix4)) # print(dataSet) ## step 2: 开始聚类... # dataSet = mat(dataSet) k = 4 centroids, clusterAssment = kmediod(dataSet, k) ## step 3: 显示聚类结果 showCluster(dataSet, k, centroids, clusterAssment) |
结果均为;
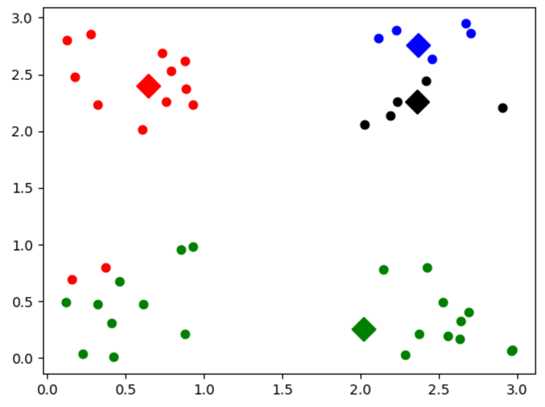
? ?
? ?
? ?
? ?
聚类算法--K-means和k-mediods/密度聚类/层次聚类
标签:次数 分配 shape 大于 plot 较差 sts 类别 info
原文地址:https://www.cnblogs.com/yifanrensheng/p/11969859.html