标签:数组 高级 img 依次 alt png 二叉树 基础 使用
数组,应该是我们每个人学习编程时接触的第一个数据结构。它很简单,但是却很重要。
很多高级的数据结构,其实都是由数组组成的,或者说是用数组来实现的。
比如跳跃表、散列表是由数组+链表组成的。
堆、完全二叉树、图(邻接矩阵存储)都可以用数组来实现。
所以说学好数组,就等于为你学习高级的数据结构打下了坚实的基础。
数组是一种线性表数据结构、它用一组连续的内存空间,来存储一组数据类型相同的数据。
这里我们来解释一下什么是线性、连续内存空间存储相同数据类型数据
线性指的是一维存储结构,比如:队列、数组、栈、链表。只有前后两个方向。
而非线性表指的是不仅仅具有前后两个方向的存储结构,比如:树、图、堆等。
因为数组占用的内存空间是连续的,所以它支持随机访问。我们只需要知道数据的存储位置,就可以以O(1)的时间复杂度访问到该元素。
首先我们先来看一下在数组是如何存储在内存中的。数据加载到内存中,内存首先会为其分配一个内存空间。计算机通过访问内存空间,来获取元素,这个过程我们称之为寻址。
计算机想要访问数组中的下标值为i的数据,只需要通过下面的寻址公式即可。
a[i]_address = base_address + i * data_type_size(首地址+偏移量*数据大小)
如果数组是一个int型数组,那么data_type_size=4。我们可以通过下标值直接访问到元素,这种访问方式,我们称之为随机访问,它的时间复杂度是 O(1)。
虽然数组的访问效率很高,但是它的拆入和删除效率却很低,O(n)
这里以插入为例,如果我们想插入一个元素,则需要将插入位置后面的元素依次移动一个位置。
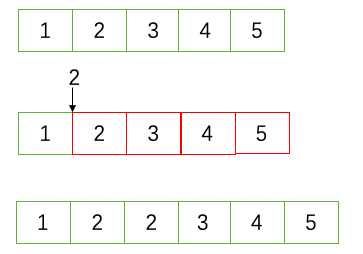
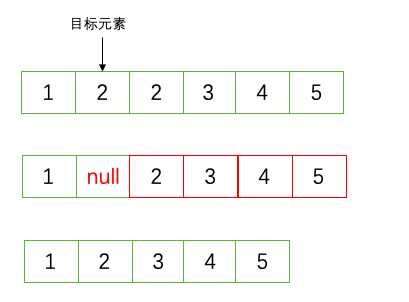
删除元素也是如此。
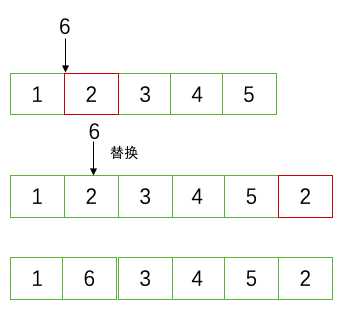
针对于插入操作,如果不要求数组内元素有序,那么每次插入操作,我们都可以将插入位置的后一个元素移动到数组末尾,然后在原位置进行插入。
这样也可以达到O(1)的时间复杂度
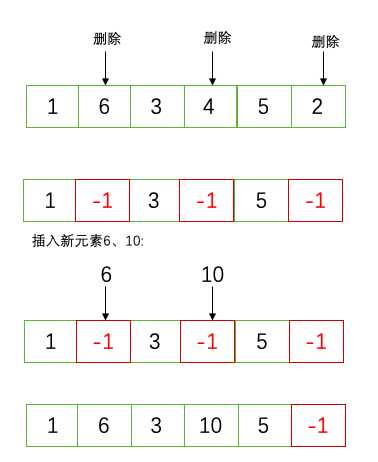
针对于删除操作,我们在删除数据的时候,可以先为被删除元素打上标记,等到数组中元素已满,再统一进行删除(JVM标记清除算法)。或者当有插入操作的时候,优先使用被标记元素的内存(Mysql中delete操作)。
答案是否定的,没有最好的数据结构,只有最适合使用的场景。
集合可以看作是一个动态数组(可扩容),底层其实也是一个数组。
下面这些场景中,我们还是更推荐使用数组:
标签:数组 高级 img 依次 alt png 二叉树 基础 使用
原文地址:https://www.cnblogs.com/nedulee/p/11979999.html