标签:nfa 数字 system rgs 取出 i++ 详细 选择 aop
原文:https://www.cnblogs.com/xiaohuiduan/p/11188304.html
下面我将以我自己的看法以及总结网上大神的经验分析各种排序的优缺点、时间空间复杂度。
选择排序
基本原理:在数组中找到最小(或最大)的元素,存到排序的起始位置,在余下的数据中再找到最小(或最大)的元素,放到已排好的元素后面。以此类推,直至所有的元素排序完毕。(注:括号中对应的是另一种情况,即元素的排序顺序为从大到小。)
public static int[] choose(int a[]){ int min; for(int i=0;i<a.length;i++){ min = i; for(int j=i+1;j<a.length;j++){ if(a[min]>a[j]){ min=j; }
//如果第一个取出来的元素不是最小值,那就交换 if(min!=i){ exchange(a,i,j); } } } } public static void exchange(int a[],int i,int j){ int temp=0; if(a[i]!=a[j]{ temp=a[i]; a[i] = a[j]; a[j] = temp; } }
选择排序的时间复杂度:
第一次排需要比较的是N-1次;
最小的元素方法第一位,下一次就不需要比较了。第二次需要比较N-2次;
第三次需要比较N-3次;
.............
第N-1次需要比较1次
总的次数为(N-1)+(N-2)+......+1=N(N-1)/2
最好的情况的所有的元素已经有序,需要交换0次。
最坏的情况是所有元素为逆序,进行交换的次数是N-1。
故时间复杂度:O(N^2)
选择排序的空间复杂度:
最好的情况是所有的元素有序,空间复杂度为O(0);
最坏的情况是所有元素为逆序,空间复杂度为O(n);
平均的空间复杂度为O(1)。
选择排序是不稳定的
插入排序
基本原理:将属组中第一个元素认为是有序数组,从前往后从第二个元素开始扫描,将元素一个个插入到那个被认为的有序的数组中,每插入一个元素,有序数组的长度加1。做法是从第二个元素往后扫描,若该元素比第一个大则不用交换,若比第一个元素小,则将该元素放置第一个元素前面,扫面第三个元素,若比首元素大而比第二个元素小,则插入其中,往后以此类推,直至所有的元素有序。
例如:
代码实现:
public class charu { public void InsertSort(){ int temp,i,j; int[] a= {38,65,97,76,13,27,49}; for( i=1;i<a.length;i++){ //外层向右的index,即作为比较对象的数据的index temp=a[i]; //用作比较的数据 int index = i-1; while(index>=0 && a[index]>temp){ //当比到最左边或者遇到比temp小的数据时,结束循环 a[index+1] = a[index]; index--; } a[index+1] = temp; } System.out.println(Arrays.toString(a)); } public static void main (String []args){ charu c = new charu(); c.InsertSort(); } }
插入排序的时间复杂度:
最好情况:元素全部有序,直接往后扫描元素都比前一个元素大,O(n)
最坏情况:元素为逆序,每次扫描都要交换位置
第一次,扫描第二个元素,发现比第一个元素小,需要比较1次,进行交换。
第二次,扫描第三个元素,发现比前两个元素都小,需要比较2次,插入到数组首个位置。
第三次,比较3次
..........
第N次,扫描第N个元素,发现比前面N-1个元素都小,需要比较N-1次,插到数组首个位置。
总共需要比较:1+2+3+.....+N-1=N(N-1)/2
时间复杂度为O(N^2)
平均情况:O(N^2)
故插入排序的时间复杂度为O(N^2)
插入排序的空间复杂度:
最好情况所有元素有序,空间复杂度O(1)
最坏情况所有元素排序为逆序,空间复杂度为O(n)
平均空间复杂度为O(1)。
插入排序是稳定的
冒泡排序
基本原理:小的数字慢慢上浮,或则大的数字慢慢下沉,上浮到最顶或则下沉到最底则结束一轮循环。每次比较相邻得的两个数值,如果前面数值大于后面数值则两者进行交换,大的数值逐渐往后移动,直至移到最后。
代码实现
public class MaoPao { public static int[] maopao(int []nums){ int len = nums.length; if(len==0||len==1){ return nums; } for(int i=0;i<len;i++){ for(int j=0;j<len-i-1;j++){ if(nums[j+1]<nums[j]){ int temp=nums[j+1]; nums[j+1] = nums[j]; nums[j] = temp; } } } return nums; } }

public class MaoPao { int nums[]={2,6,7,1,9,4,3}; public void maopao(){ int len = nums.length; if(len==0||len==1){ return ; } for(int i=0;i<len;i++){ for(int j=0;j<len-i-1;j++){ if(nums[j+1]<nums[j]){ int temp=nums[j+1]; nums[j+1] = nums[j]; nums[j] = temp; } } } System.out.println(Arrays.toString(nums)); } public static void main(String []args){ MaoPao mao = new MaoPao(); mao.maopao(); } }
冒泡排序的时间复杂度:
最坏情况:我们想要从小到大而数组却是从大到小,事先未知,那么
第一轮,将最小的数字移动到数组首位置,要比较的个数为N-1;
第二轮,将第二小的数字移动到首位置后,要比较的个数为N-2;
..........
第N轮,将倒数第二小的数字移动到最大数字前面,要比较的个数为1个。
总共要比较的个数为:(N-1)+(N-2)+.......+1=N(N-1)/2。
故最坏的情况时间复杂度为O(N^2)。
最好的情况:元素全部有序,从小到大排好,做N-1次比较。时间复杂度为O(N)。
平均时间复杂度为O(N^2)。
冒泡排序是稳定的排序算法。
快速排序
基本原理:在数组中选取一个数(一般是第一个数),分别与其它每一个数进行比较,把比这个数小的都放到它前面,把比这个数大的都放到它后面,放完后数组就分成两部分,以刚开始选取的那个数为界,往前的数都比它小,往后的数都比它大,然后分别对这两个部分进行递归排序算法,就可以实现整个数组的排序。
详细过程:数组首个数为基准数,设置两个哨兵left(指向数组首个元素)和right(指向数组末尾元素),先让right往右移动,找到比基准数小的数字就停住,然后left开始往左移动,找个比基准数大的数字就停住,left所指的数字与right所指的数字交换,继续移动(同样的是right先移动)。当right=left即两个哨兵相遇时,停止移动,将相遇点的元素与基准数相交换,这样刚开始的基准数就“归位了”,左边的元素必然比基准数小,右边的元素必然比基准数大。递归调用,新的数组以首个元素为基准数设为left,“归位后”的元素为right,重复上面的步骤。直至所有的元素有序。
代码实现:
package suanfa; public class KuaiSuPai { public static void quickSort(int[] arr,int left,int right){ int i,j,temp,t; if(left>right) return; temp=arr[left];//temp存的就是基准数 i=left; j=right; while(i!=j){ //顺序很重要,从右往坐找 while(arr[j]>=temp && i<j) j--; //再从左往右找 while(arr[i]<=temp && i<j) i++; //交换两个数在数组中的位置 if(i<j)//让哨兵i和j没有相遇时 { t=arr[i]; arr[i]=arr[j]; arr[j]=t; } } //最终将基准数归位 arr[left]=arr[i]; arr[i]=temp; quickSort(arr,left,i-1); quickSort(arr,i+1,right); return; } public static void main(String []args){ int []arr = {10,7,2,4,7,62,3,4,2,1,8,9,19}; quickSort(arr,0,arr.length-1);//调用快速排序,left=0,right为最右端数字 for(int i=0;i<arr.length;i++){ System.out.println(arr[i]); } } }
快速排序的时间复杂度:
最好的情况:元素有序
递归算法的时间复杂度公式:T[n] = aT[n/b] + f(n) ;
第一次递归比较次数:T[n] = 2T[n/2] + n
第二次递归比较次数:令n=n/2代入上式得 2^2 T[ n/ (2^2) ] + 2n
第三次递归比较次数: 2^3 T[ n/ (2^3) ] + 3n
.............
令:n = n/( 2^(m-1) ) = 2^m T[1] + mn ----------------第m次递归(m次后结束)
当最后平分的不能再平分时,也就是说把公式一直往下跌倒,到最后得到T[1]时,说明这个公式已经迭代完了(T[1]是常量了)。
得到:T[n/ (2^m) ] = T[1] ===>> n = 2^m ====>> m = logn;
T[n] = 2^m T[1] + mn ;其中m = logn;
T[n] = 2^(logn) T[1] + nlogn = n T[1] + nlogn = n + nlogn ;其中n为元素个数
又因为当n >= 2时:nlogn >= n (也就是logn > 1),所以取后面的 nlogn;
综上所述:快速排序最优的情况下时间复杂度为:O( nlogn )
计算来源:https://blog.csdn.net/A_BlackMoon/article/details/81064712
最坏情况时间复杂度:O(N^2)
最差的情况就是每一次取到的元素就是数组中最小/最大的,这种情况其实就是冒泡排序了(每一次都排好一个元素的顺序)
这种情况时间复杂度就好计算了,就是冒泡排序的时间复杂度:T[n] = n * (n-1) = n^2 + n;
堆排序:
堆排序的基本原理:将无序的序列构建成一个堆,根据升序降序的需求选择大顶堆或者小顶堆。将堆顶元素与末尾元素交换,将最大的元素沉至数组末端。重新调整结构使其满足堆的定义,然后继续交换堆顶元素和当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
代码实现
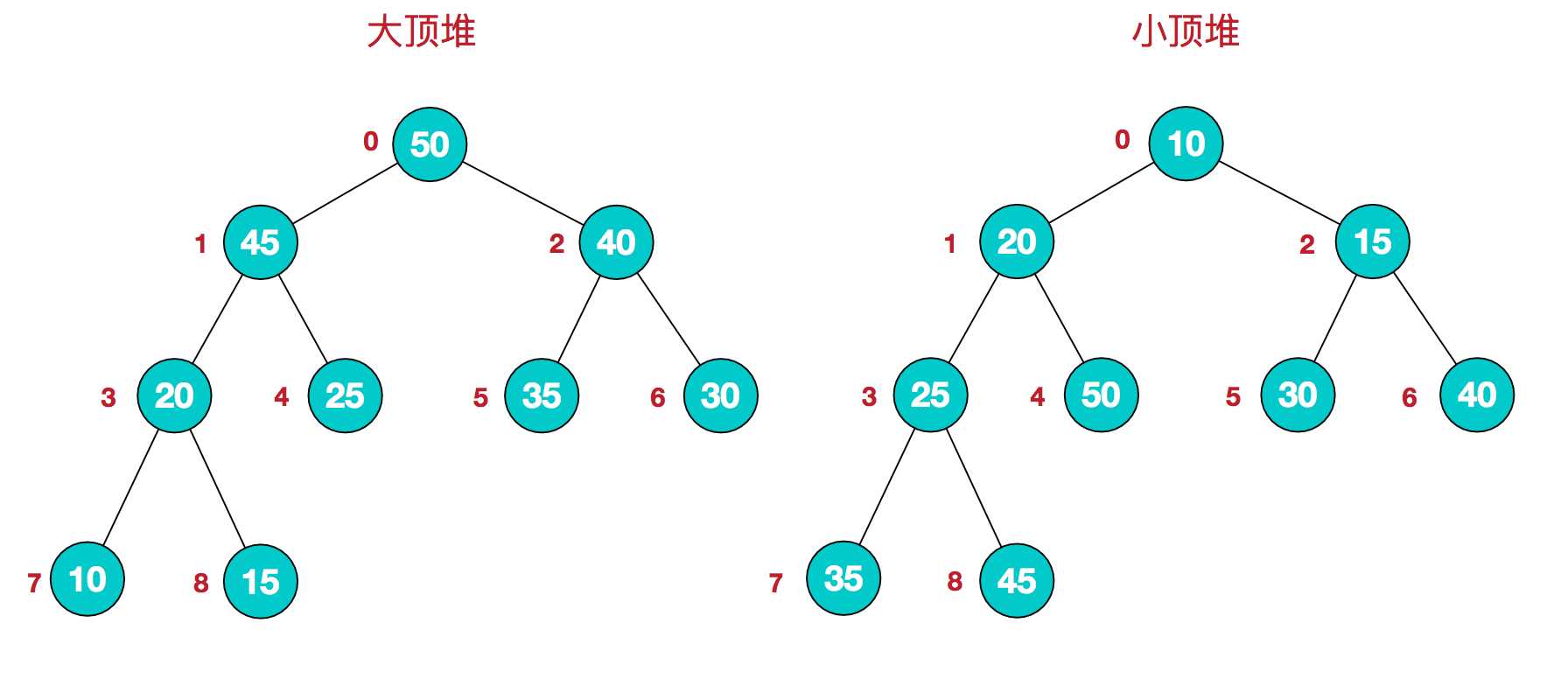
了解大堆顶和小堆顶的区别
标签:nfa 数字 system rgs 取出 i++ 详细 选择 aop
原文地址:https://www.cnblogs.com/hjdk05/p/11968501.html