标签:style blog http color os ar sp 数据 on
给定训练集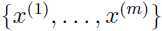 ,我们希望构建该数据联合分布
,我们希望构建该数据联合分布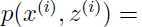
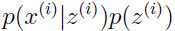
这里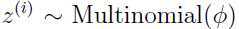 ,其中
,其中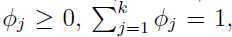
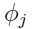 是概率
是概率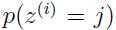 ,并且
,并且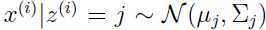 ,用
,用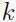 表示
表示 可能的取值。
可能的取值。
因此,我们构建的模型就是假设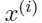 是由
是由 生成,而
生成,而 是从
是从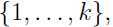 中随机选择出来的,那么
中随机选择出来的,那么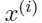 就服从
就服从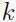 个依赖于
个依赖于 的高斯分布中的一个。这就是高斯混合模型。
的高斯分布中的一个。这就是高斯混合模型。
 是潜在随机变量,即它是隐藏的或者观察不到的,这将使得估计问题变得棘手。
是潜在随机变量,即它是隐藏的或者观察不到的,这将使得估计问题变得棘手。
上面公式太多,作一个总结,总体意思是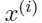 关于
关于 的条件分布符合高斯分布(即正态分布),这个
的条件分布符合高斯分布(即正态分布),这个 是潜在变量,它的值未知,但是
是潜在变量,它的值未知,但是 服从多项式分布,于是
服从多项式分布,于是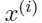 关于
关于 的条件分布就是高斯混合模型,而
的条件分布就是高斯混合模型,而 是一个潜在变量,值不确定,进而导致高斯混合模型的概率估计也变得棘手。
是一个潜在变量,值不确定,进而导致高斯混合模型的概率估计也变得棘手。
可以看出,我们构建的高斯混合模型参数有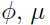 和
和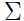 ,为了估计出这些参数,写出参数的似然函数:
,为了估计出这些参数,写出参数的似然函数:
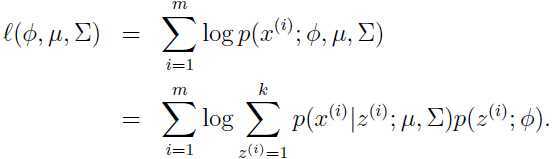
变量 意味着每一个
意味着每一个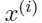 来自于
来自于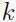 个高斯分布中的哪一个,如果我们知道变量
个高斯分布中的哪一个,如果我们知道变量 的值,最大化似然函数问题将变得容易,似然函数将会变成如下形式:
的值,最大化似然函数问题将变得容易,似然函数将会变成如下形式:
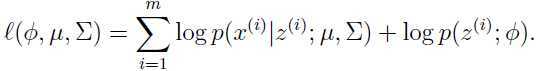
那么参数的最大似然估计可以计算出:
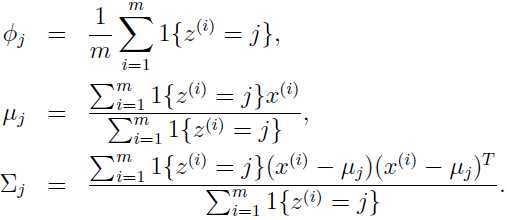
可以看出,当 已知的时候,最大似然函数的的估计与前面讨论过的高斯判别分析模型(关于高斯判别模型参见生成式学习算法)几乎一样,除了这里
已知的时候,最大似然函数的的估计与前面讨论过的高斯判别分析模型(关于高斯判别模型参见生成式学习算法)几乎一样,除了这里 替代了高斯判别模型中类别标签的角色。
替代了高斯判别模型中类别标签的角色。
但是在这个问题中 是未知的,该怎么办?就得运用EM算法。在应用到我们的这个问题中,EM算法分两步,在E步骤中,算法试图猜测出
是未知的,该怎么办?就得运用EM算法。在应用到我们的这个问题中,EM算法分两步,在E步骤中,算法试图猜测出 的值,在M步骤中,根据E步骤猜测的值更新参数。需要注意的是在M步骤中假定E步骤中的猜测是正确的,算法流程如下:
的值,在M步骤中,根据E步骤猜测的值更新参数。需要注意的是在M步骤中假定E步骤中的猜测是正确的,算法流程如下:
E-step: 对于每一个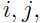 ,令:
,令:
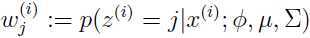
M-step: 更新参数:
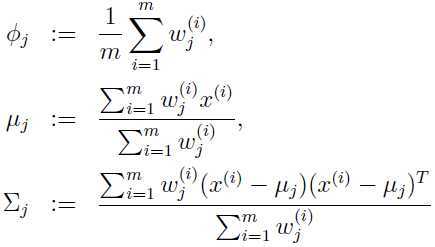
重复上面两步直至收敛(参数不再发生明显变化)
在E-step中计算 关于
关于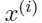 的后验概率时,参数
的后验概率时,参数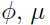 和
和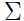 用的都是当前的值,第一步时可以随机初始化,用贝叶斯公式,我们可以得到:
用的都是当前的值,第一步时可以随机初始化,用贝叶斯公式,我们可以得到:
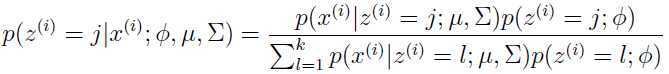
分子上的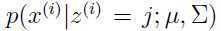 是由均值为
是由均值为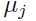 ,方差为
,方差为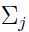 的高斯分布在
的高斯分布在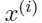 处的概率密度给出,
处的概率密度给出,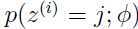 由参数
由参数
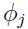 给出. 在E-step中对
给出. 在E-step中对 的猜测只是猜测它是某个值得概率,被称作“软猜测”,与之对应的“硬猜测”就是一个最好的猜测,即不是0就是1.
的猜测只是猜测它是某个值得概率,被称作“软猜测”,与之对应的“硬猜测”就是一个最好的猜测,即不是0就是1.
和上面我们在推导 已知时,参数估计的公式相比,EM算法中的参数更新仅仅是用
已知时,参数估计的公式相比,EM算法中的参数更新仅仅是用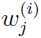 代替了
代替了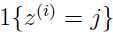 .
.
EM算法和k-means算法(参考我的博文K-means聚类算法原理和C++实现)很类似,除了k-means是一个“硬” 类别分配(为每个样本选择一个确定的类别),而这里是以概率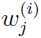 的“软”分配(就是
的“软”分配(就是 取某个值的概率)。同k-means一样,EM算法也容易陷入局部最优,所以多次运行,每次都将参数初始化为不同的值将会是一个很好的解决办法。
取某个值的概率)。同k-means一样,EM算法也容易陷入局部最优,所以多次运行,每次都将参数初始化为不同的值将会是一个很好的解决办法。
EM算法就是不断重复猜测 的值,但是到底是如何进行的呢,如何保证收敛性呢,在下一篇博文将继续讨论,从而使得EM算法能够更加容易应用到各种存在潜在变量的参数估计问题中,而且将讨论如何保证算法收敛。
的值,但是到底是如何进行的呢,如何保证收敛性呢,在下一篇博文将继续讨论,从而使得EM算法能够更加容易应用到各种存在潜在变量的参数估计问题中,而且将讨论如何保证算法收敛。
标签:style blog http color os ar sp 数据 on
原文地址:http://www.cnblogs.com/90zeng/p/Mixtures_of_Gaussians_and_the_EM_algorithm.html