监督学习的Logistic回归算法

标签：问题   strong   tps   思想   分类   二分   表示   begin   roc   

函数原型

\[h_\theta(X)=\frac{1}{1+e^{-\theta^TX}}...称h_\theta(X)为y=1的概率。\]

决策界限的定义

\(根据函数表达式可知当z>=0时y>=0.5当z<0时y<0.5...z=\theta^TX,y=h_\theta(X)\)

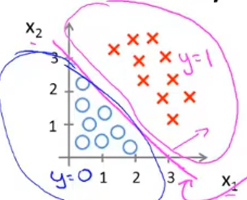
\(故直线z=\theta^TX为决策界限\)
## 代价函数
线性回归的代价函数为：
\[J(\theta)=2\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^i)-y(x^i))^2\]
我们另：
\[J(\theta)=\frac{1}{m}\sum_{i=1}^{m}Cost(h_\theta(x^i),y(x^i))\]
\(Cost为：\)
\[Cost(h_\theta(x^i),y(x^i))=\begin{cases} -log(h_\theta (x))& \text if&y=1\\-log(1-h_\theta (x))& \text if&y=0\end{cases}\]
为什么这样选择？
#### \(-log(1-h_\theta (x))图像为：\)

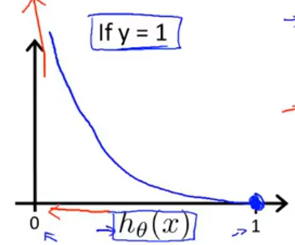
其中\[h_\theta(X)=\frac{1}{1+e^{-\theta^TX}}.\]
当\(h_\theta (x)\)无限靠近与0时，代价函数为无穷大。
故\(h_\theta (x)=0表示y=1的概率为0，与条件y=1完全矛盾。故给该算法加大惩罚。\)

当\(h_\theta (x)\)无限靠近与1时，代价函数为0。
故\(h_\theta (x)=1表示y=1的概率为100\%，与条件y=1完全符合。\)

#### \(-log(1-h_\theta (x))图像为：\)

证明方式与图1类似...

合并代价函数

\[J(\theta)=\frac{1}{m}\sum_{i=1}^m(-ylog(h_{\theta}(x^i))-(1-y)log(1-h_{\theta}(x^i)))\]

使用梯度下降法迭代

公式与线性回归公式相同。
证明参考：https://blog.csdn.net/qq_29663489/article/details/87276708

多分类问题

思想：二分，归类于y=1概率的的一类。
如图，三个函数同时处理，得到\(h_\theta(X)\)，故点归类于\(h_\theta(X)\)大的一类。

监督学习的Logistic回归算法

标签：问题   strong   tps   思想   分类   二分   表示   begin   roc   

原文地址：https://www.cnblogs.com/Kseven77/p/12019385.html