标签:off tao else 取出 color mat 那是 set stride
最近看到一篇文章讲IMAGE DECOMPOSITION,里面提到了将图像分为Texture layer和Structure layer,测试了很多方法,对于那些具有非常强烈纹理的图像,总觉得用TV去燥的方法分离的结果都比其他的方法都要好(比如导向、双边),比如下图:


再比如:


可见TV可以把纹理很好的提取出来。
现在应该能找到很多的TV代码,比如IPOL上就有,详见 http://www.ipol.im/pub/art/2013/61/。
我在其他地方也见过一些,比如这里: http://yu-li.github.io/paper/li_eccv14_jpeg.zip,他是借助于FFT实现的,当然少不了多次迭代,速度也是比较慢的。
我还收藏了很久前一位朋友写的M代码,但是现在我不知道把他QQ或者微信弄到哪里去了,也不知道他会不会介意我把他的代码分享出来。
function dualROF()
clc
f0=imread(‘rr.bmp‘);
f0=f0(:,:,1);
[m,n]=size(f0);
f0=double(f0);
lamda=30; % smoothness paramter, the larger the smoother
tao=.125; % fixed do not change it.
p1=zeros(m,n);
p2=zeros(m,n);
tic
for step=1:100
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
div_p=div(p1,p2);
cx=Fx(div_p-f0/lamda);
cy=Fy(div_p-f0/lamda);
abs_c=sqrt(cx.^2+cy.^2);
p1=(p1+tao*cx)./(1+tao*abs_c);
p2=(p2+tao*cy)./(1+tao*abs_c);
end
u=f0-lamda*div_p;
toc
figure; imagesc(f0); colormap(gray); axis off; axis equal;
figure; imagesc(u); colormap(gray); axis off; axis equal;
% Compute divergence using backward derivative
function f = div(a,b)
f = Bx(a)+By(b);
% Forward derivative operator on x with boundary condition u(:,:,1)=u(:,:,1)
function Fxu = Fx(u)
[m,n] = size(u);
Fxu = circshift(u,[0 -1])-u;
Fxu(:,n) = zeros(m,1);
% Forward derivative operator on y with boundary condition u(1,:,:)=u(m,:,:)
function Fyu = Fy(u)
[m,n] = size(u);
Fyu = circshift(u,[-1 0])-u;
Fyu(m,:) = zeros(1,n);
% Backward derivative operator on x with boundary condition Bxu(:,1)=u(:,1)
function Bxu = Bx(u)
[~,n] = size(u);
Bxu = u - circshift(u,[0 1]);
Bxu(:,1) = u(:,1);
Bxu(:,n) = -u(:,n-1);
% Backward derivative operator on y with boundary condition Bxu(1,:)=u(1,:)
function Byu = By(u)
[m,~] = size(u);
Byu = u - circshift(u,[1 0]);
Byu(1,:) = u(1,:);
Byu(m,:) = -u(m-1,:);
M的代码,代码量不大,那是因为Matlab的向量化确实很厉害,但是这个代码还是很慢的,256*256的灰度图迭代100次都要700ms了。
这里抛开一些优化不说,用这个circshift会造成很大的性能损失,我们稍微分析下就能看到用这个地方其实就是简单的水平或者垂直方向的差分,完全没有必要这样写。
直接按照代码的意思用C语言把他们展开并不做其他的优化可得到大概下面这种不怎么好的代码:
int IM_DualTVDenoising(unsigned char *Src, unsigned char *Dest, int Width, int Height, int Stride, float Lamda = 20 , int Iter = 20)
{
int Channel = Stride / Width;
if ((Src == NULL) || (Dest == NULL)) return IM_STATUS_NULLREFRENCE;
if ((Width <= 0) || (Height <= 0)) return IM_STATUS_INVALIDPARAMETER;
if ((Channel != 1) && (Channel != 3) && (Channel != 4)) return IM_STATUS_INVALIDPARAMETER;
if (Channel == 1)
{
float tao = 0.125; // fixed do not change it.
float InvLamda = 1.0 / Lamda;
float *p1 = (float *)malloc(Width * Height * sizeof(float));
float *p2 = (float *)malloc(Width * Height * sizeof(float));
float *div_p = (float *)malloc(Width * Height * sizeof(float));
float *cx = (float *)malloc(Width * Height * sizeof(float));
float *cy = (float *)malloc(Width * Height * sizeof(float));
float *Temp = (float *)malloc(Width * Height * sizeof(float));
int X, Y;
float q1, q2, q, abs_c;
float *LineP1, *LineP2, *LineP3, *LineP4;
unsigned char *LinePS, *LinePD;
for (int Z = 0; Z < Iter; Z++)
{
//Div(p1, p2, div_p);
for (Y = 0; Y < Height; Y++)
{
LineP1 = p1 + Y * Width; //Fx(Temp, cx);
LineP2 = cx + Y * Width;
LineP2[0] = LineP1[0];
for (X = 1; X < Width; X++)
{
LineP2[X] = LineP1[X] - LineP1[X - 1];
}
LineP2[Width - 1] = -LineP1[Width - 2];
}
memcpy(cy, p2, Width * sizeof(float));
for (Y = 1; Y < Height; Y++)
{
LineP1 = (float *)(p2 + (Y - 1)* Width);
LineP2 = (float *)(p2 + Y * Width); //Fy(Temp, cy);
LineP3 = (float *)(cy + Y * Width);
for (X = 0; X < Width; X++)
{
LineP3[X] = LineP2[X] - LineP1[X];
}
}
LineP1 = (float *)(p2 + (Height - 2) * Width);
LineP2 = (float *)(cy + (Height - 1) * Width);
for (X = 0; X < Width; X++)
{
LineP2[X] = -LineP1[X];
}
for (Y = 0; Y < Height; Y++)
{
LineP1 = (float *)(cx + Y * Width);
LineP2 = (float *)(cy + Y * Width); //Fy(Temp, cy);
LineP3 = (float *)(div_p + Y * Width);
for (X = 0; X < Width; X++)
{
LineP3[X] = LineP1[X] + LineP2[X];
}
}
for (Y = 0; Y < Height; Y++)
{
LineP1 = (float *)(div_p + Y * Width);
LineP2 = (float *)(Temp + Y * Width);
LinePS = Src + Y * Stride;
for (X = 0; X < Width; X++)
{
LineP2[X] = LineP1[X] - LinePS[X] * InvLamda;
}
}
for (Y = 0; Y < Height; Y++)
{
LineP1 = (float *)(Temp + Y * Width); //Fx(Temp, cx);
LineP2 = (float *)(cx + Y * Width);
for (X = 0; X < Width - 1; X++)
{
LineP2[X] = LineP1[X + 1] - LineP1[X];
}
LineP2[Width - 1] = 0;
}
for (Y = 0; Y < Height - 1; Y++)
{
LineP1 = (float *)(Temp + Y * Width);
LineP2 = (float *)(Temp + (Y + 1) * Width); //Fy(Temp, cy);
LineP3 = (float *)(cy + Y * Width);
for (X = 0; X < Width; X++)
{
LineP3[X] = LineP2[X] - LineP1[X];
}
}
memset(Temp + (Height - 1) * Width, 0, Width * sizeof(float));
for (Y = 0; Y < Height; Y++)
{
LineP1 = (float *)(p1 + Y * Width);
LineP2 = (float *)(p2 + Y * Width);
LineP3 = (float *)(cx + Y * Width);
LineP4 = (float *)(cy + Y * Width);
for (X = 0; X < Width; X++)
{
abs_c = sqrt(LineP3[X] * LineP3[X] + LineP4[X] * LineP4[X]);
abs_c = 1 / (1 + tao * abs_c);
LineP1[X] = (LineP1[X] + tao * LineP3[X]) * abs_c;
LineP2[X] = (LineP2[X] + tao * LineP4[X]) * abs_c;
}
}
}
for (Y = 0; Y < Height; Y++)
{
LineP1 = (float *)(div_p + Y * Width);
LinePS = Src + Y * Stride;
LinePD = Dest + Y * Stride;
for (X = 0; X < Width; X++)
{
LinePD[X] = IM_ClampToByte((int)(LinePS[X] - Lamda * LineP1[X]));
}
}
free(p1);
free(p2);
free(div_p);
free(cx);
free(cy);
free(Temp);
}
else
{
}
}
算法明显占用很大的内存,而且看起来别扭,不过速度还是杠杠的,256*256的灰度图迭代100次都要30ms了。反编译看了下代码,编译器对代码做了很好的SIMD指令优化。
上面的C语言还是可以继续优化的,这就需要大家自己的认真的去研读代码深层次的逻辑关系了,实际上可以只要上面的一半的临时内存的,而且很多计算可以集中在一个循环里完成,可以手动内嵌SIMD指令,或者直接使用编译器的优化能力,基本上这样的简单的算法逻辑编译器编译后的速度不会比我们手写的SIMD指令慢,有的时候还是会快一些,不得不佩服那些写编译器的大牛。优化后的速度大概在14ms左右。
研究TV算法需要很好的数学功底,以前朋友曾经给我寄过一本书,里面都是微分方面的数学公式,看的我吓死了,不过TV算法似乎有很多很好的应用,也曾经流行过一段时间,可惜现在深度学习一出来,很多人都喜欢这种直接从海量数据中建造黑盒模型,而对那些有着很明显的数学逻辑的算法嗤之以鼻了,真有点可惜。
以前在基于总变差模型的纹理图像中图像主结构的提取方法 一文中曾提到那个论文附带的Matlab代码没有什么意义,因为他很难转换成C的代码,即时转换成功了,也处理不了大图,但是本文这里的TV算法总的来说在内存占用或者速度方面都还令人满意。
在去噪效果上,这个算法还算可以:
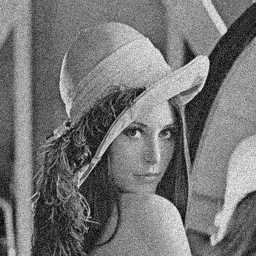



本文Demo下载地址: http://files.cnblogs.com/files/Imageshop/SSE_Optimization_Demo.rar, 算法位于Denoise --> TV Denoising下。
【算法随记六】一段Matlab版本的Total Variation(TV)去噪算法的C语言翻译。
标签:off tao else 取出 color mat 那是 set stride
原文地址:https://www.cnblogs.com/Imageshop/p/12051536.html