标签:不能 计算 传输过程 发送 出现 http cci word src
CRC校验原理
CRC校验其根本思想
a.发送端和接收端约定一个整数 b
b.发送端在原始数据帧后面附加一个数 k ,产生一个新的数据帧
c.接收端接收到数据帧后,对接收的数据帧和整数 b 进行位异或操作,如果异或的结果是 0 ,表明数据完整,否则数据丢失
关键点1:整数 b 的选择
整数 b 随机选择,也可按国际上通行的标准选择,但最高位和最低位必须均为“1”,
如在IBM的SDLC(同步数据链路控制)规程中使用的CRC-16(也就是这个除数一共是17位)生成多项式g(x)= x^16 + x^15 + x^2 + 1(对应二进制比特串为:11000000000000101);
而在ISO HDLC(高级数据链路控制)规程、ITU的SDLC、X.25、V.34、V.41、V.42等中使用CCITT-16生成多项式g(x)= x^16 + x^15 + x^5 + 1(对应二进制比特串为:11000000000100001)。
关键点2:附加数 k 计算
假设选定的除数b二进制位数(假设为m位),然后在要发送的数据帧(假设为n位)后面加上m-1位 0 ,新的数据帧使用 "模2除法(模2除法就是n次循环移位异或运算异或运算,并非数学除法)" 除以上面这个除数
,所得到的余数 k(也是二进制的比特串)就是该帧的CRC校验码,也称之为FCS(帧校验序列),强调余数 k 的位数一定要是比除数 b 位数只能少一位,哪怕前面位是0,
甚至是全为0(附带好整除时)也都不能省略。
示例:
现假设选择的CRC生成多项式为G(X) = X^4 + X^3 + 1,要求出二进制序列1001010110011的CRC校验码。下面是具体的计算过程:
a.计算整数 b ,根据多项式,得出 b = 11001,推断出附加数 k 是4位
b.原始数据帧末尾补位 k 个0,得出新数据 10101100110000 ,对新数据进行 模2除法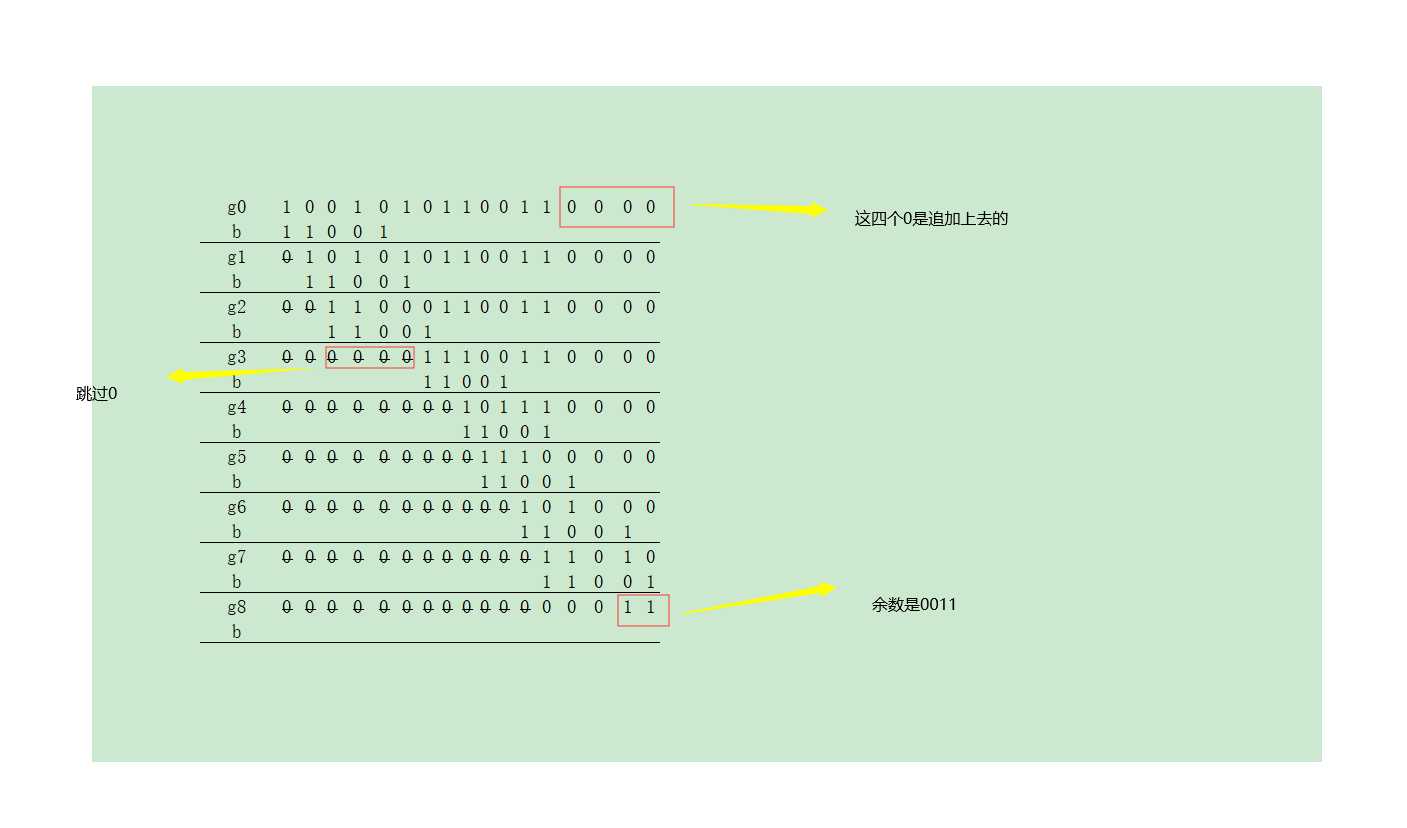
c.计算出余数 k 的值是 100,不满足4位,补0,计算出的k的最终值是 0100
d.把上步计算得到的CRC校验0100替换原始帧101100110000后面的四个 0 ,得到新帧101100110100。再把这个新帧发送到接收端。
e.以上新帧到达接收端后,接收端会把这个新帧再用上面选定的除数 11001 以 "模2除法" 方式去除,验证余数是否为0,如果为0,则证明该帧数据在传输过程中没有出现差错,否则出现了差错。
常用标准
CRC-16 (x^16 + x^15 + x^2 + 1 ) 1,1000,0000,0000,0101
CRC-32 (x^32 + x^26 + x^23 + x^22 + x^16 + x^12 + x^11 + x^10 + x^8 + x^7 + x^5 + x^4 + x^2 + x + 1) 1,0000,0100,1100,0001,0001,1101,1011,0111
标签:不能 计算 传输过程 发送 出现 http cci word src
原文地址:https://www.cnblogs.com/zhanggaofeng/p/12063542.html