标签:欧几里得 拓展欧几里得 gcd 拓展gcd 线性同余方程
最大公约数的求法中最过著名的莫过于欧几里得辗展相除法,它有两种形式(递归与非递归,其实是一样的,任何递归都可以写成非递归),下面看看GCD的实现代码:
設

欲證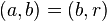
先設
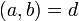


可得 且知
且知
表示d是b,r的公因數,但
所以
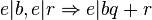
可得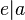 且知
且知
表示e是a,b的公因數,但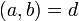
所以
由 可得知
可得知

扩展的欧几里德算法是求如a * x + b * y = (a, b) 这样的整数解的,可以仿照欧几里德算法得出答案。程序如下:
上述程序只是得到了一组解,很显然解是不唯一的:x增加b, y减少a一定是原方程的一组解:
a * (x + b) + b * (y - a) = a * x + b * y = (a, b)。
然而在应用上,往往并不是如此简单,很多时候会求解不定方程a * x + b * y = n。这个时候还是应用上面的算法:
/*
扩展欧几里得定理
扩展欧几里得定理:对于两个不全为0的整数a、b,必存在一组解x,y,
使得ax+by==gcd(a,b);
拓展欧几里得实现
下面面的程序中,x和y用全局变量保存
int gcd(int a,int b)
{
int t,d;
if(b==0)
{
x=1;
y=0;
//此时b==0,也就是说gcd(a,0)==a。原式变为ax+by==a=gcd(a,b)--> x==1,y==0
return a; //返回a,b最大公约数的值
}
d=gcd(b,a%b); //欧几里得求最大公约数应用
t=x;
x=y;
y=t-(a/b)*y; //不明处2
return d; //返回a,b最大公约数的值
}
//不明处2 解释 ax+by==gcd(a,b)(1)
说明规则,x,y表示第一次递归时的值,x1,y1表示第二次递归时的值。
那么gcd(a,b)==gcd(b,a%b),同时都代入式1,
有ax+by==b*x1+(a%b)*y1。将右边变形一下
b*x1+(a%b)*y1==b*x1+(a-(a/b)*b)*y1==a*y1+b*(x1-(a/b)*y1),
最终得到ax+by==a*y1+b*(x1-(a/b)*y1)
也就是说:
上一深度的x等于下一深度的y1,
上一深度的y等于下一深度的x1-(a/b)*y1。
*需要注意,上面推导时用的除法都是整型除法
因此,得到了不定式ax+by==gcd(a,b)的一组解,x、y。
那么对于一般的不定式ax+by==c,它的解应该是什么呢。
很简单,x1=x*(c/gcd(a,b)),y1=y*(c/gcd(a,b))
再深入一点,就解出这么一组解其实一般来说是解决不了什么问题的,
我们现在要得到所有的解,那么这所有的解究竟是什么呢?
假设d=gcd(a,b). 那么x=x0+b/d*t; y=y0-a/d*t;其中t为任意常整数。
*/
#include<stdio.h>
#include<stdlib.h>
/*
求关于 x 的同余方程 ax ≡ 1 (mod b)的最小正整数解。
即求ax=mb+r 1=nb+r
变形ax+(n-m)b=1,此方程即拓展欧几里德的应用ax+by=gcd(a,b),(n-m相当于y)
事实上ax ≡1(mod b) 有解的必要条件是gcd(a,b)|1,即gcd(a,b)=1;
使用拓展欧几里得可知 ax+by=1(x,y是整数)
*/
int Extragcd(int a,int b,int *x,int *y)
{
int d,t;
if(b==0) //递归调用终止条件,当根据欧几里得辗转相除法则,余数为0停止
{
*x=1;
*y=0;
return a;
}
else
{
d=Extragcd(b,a%b,x,y);
t=*x; //根据下一个x1,y1的值,倒推前一个x,y的值
*x=*y;
*y=t-a/b*(*y);
return d;
}
}
int main()
{
int a,b,x,y;
int ans;
freopen("mod.in","r",stdin);
freopen("mod.out","w",stdout);
scanf("%d%d",&a,&b);
ans=Extragcd(a,b,&x,&y);
if(ans!=1) return 0;
//根据若x是方程的一个解,则方程的所有解为x+k*b k为整数
x=x%b; //保证最小的正整数解x ,且x属于{0,1,2,3...b-1}
while(x<=0)
x+=b ;
printf("%d\n",x);
return 0;
}
标签:欧几里得 拓展欧几里得 gcd 拓展gcd 线性同余方程
原文地址:http://blog.csdn.net/txl199106/article/details/40653615