标签：height   数据   col   建立   基本概念   数组   后继节点   ima   idt   

排序二叉树

一、基本概念

二叉树是一种从上往下的树状结构的数据结构，从根节点开始每个节点最多有两个子节点，

左边的为左子节点，右边的为右子节点。

排序二叉树--有顺序，且没有重复元素的二叉树。顺序为：

对每个节点而言：

1）如果左子树不为空，则左子树上的所有节点都小于该节点；

2）如果右子树不为空，则右子树上的所有节点都大于该节点；

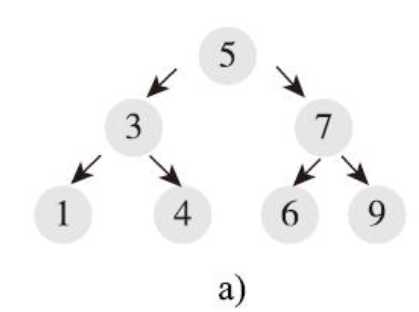
如图，根节点为5，左边的节点都大于5，右边的节点都小于5。

二、基本算法

1.查找

1）首先与根节点比较，相同则找到；

2）如果小于根节点，则到左子树种递归查找；

3）如果大于根节点，则到右子树中递归查找；

这个步骤与在数组中进行二分查找是类似的。此外，在排序二叉树中查找最大值和最小值很简单。

2.遍历

排序二叉树可以方便的按序遍历，用递归的方式。

如下图的例子，先访问根节点的左子树，一直到最左边的节点--1，1没有右子树

，返回上一层，访问3，然后访问3的右子树，4没有左子树，所以访问4，然后4的右

子树6，以此类推。1--3--4--6--7--8--9

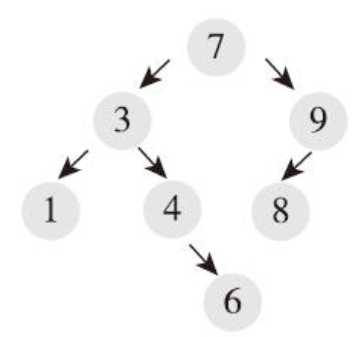
 不用递归的方式，也可以实现按序遍历：第一个节点为最左边的节点，从第一个

节点开始，依次找后继节点，找其后继节点的算法为：

1）如果该节点有右子节点，则后继节点为右子树中的最小节点；

2）如果该节点无右子节点，则后继节点为父节点或者某个祖先节点，

从当前节点往上找，如果它是父节点的右孩子，则继续找父节点，直到

它不是右孩子或父节点为空，第一个非右孩子节点的父节点就是后继节点，

如果找不到这样的祖先节点，则后继为空，遍历结束。

3.插入

在排序二叉树中，插入元素首先要找插入位置，即新节点的父节点。

与查找元素类似从根节点开始找：

1）与当前节点相同，则已经存在了，不能插入；

2）如果小于当前节点，则到左子树中查找，如果左子树为空，则当前节点为要找到的父节点；

3）如果大于当前节点则到右子树中查找，如果右子树为空，则当前节点为要找的父节点。

 3.删除

从排序二叉树中删除一个节点，主要有三种情况：

1）节点为叶子节点: 直接删除

2）节点只有一个孩子节点：

删除当前节点，让其子节点与父节点建立链接。

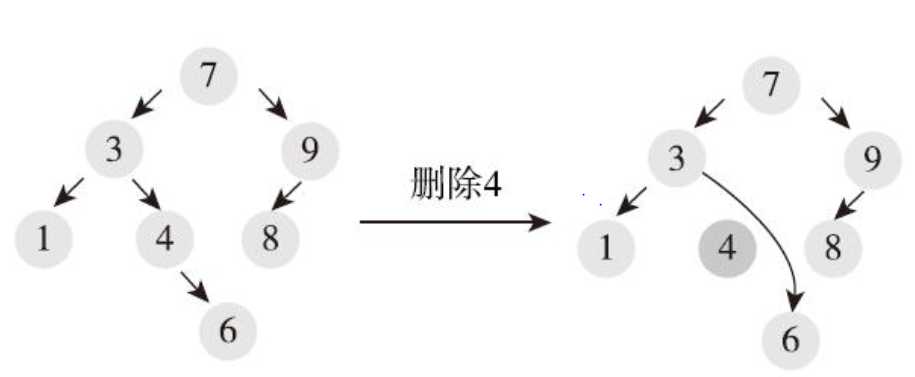
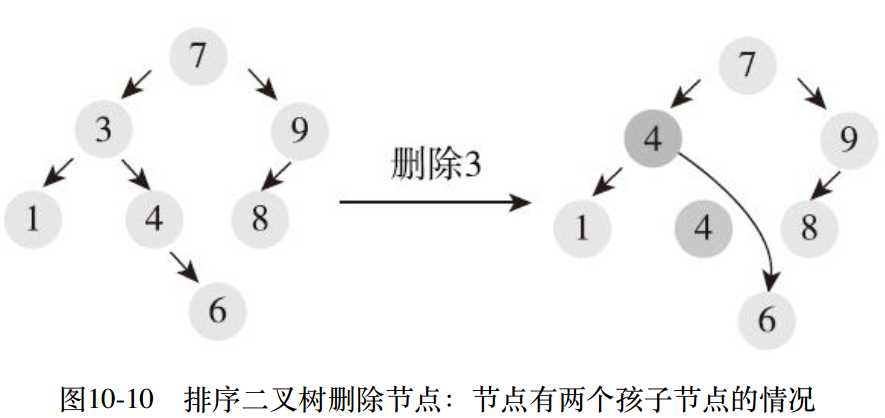
3）节点有两个孩子节点：

排序二叉树

标签：height   数据   col   建立   基本概念   数组   后继节点   ima   idt   

原文地址：https://www.cnblogs.com/Shadowplay/p/10000707.html