回溯算法

标签：解答   https   规律   hellip   result   img   其它   拓展   计算   

Wiki解释

回溯法（英语：backtracking）是暴力搜索法中的一种。

对于某些计算问题而言，回溯法是一种可以找出所有（或一部分）解的一般性算法，尤其适用于约束满足问题（在解决约束满足问题时，我们逐步构造更多的候选解，并且在确定某一部分候选解不可能补全成正确解之后放弃继续搜索这个部分候选解本身及其可以拓展出的子候选解，转而测试其他的部分候选解）。

在经典的教科书中，八皇后问题展示了回溯法的用例。（八皇后问题是在标准国际象棋棋盘中寻找八个皇后的所有分布，使得没有一个皇后能攻击到另外一个。）

回溯法采用试错的思想，它尝试分步的去解决一个问题。在分步解决问题的过程中，当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现，在反复重复上述的步骤后可能出现两种情况：

• 找到一个可能存在的正确的答案
• 在尝试了所有可能的分步方法后宣告该问题没有答案

在最坏的情况下，回溯法会导致一次复杂度为指数时间的计算。

除此之外，很多经典的数学问题都可以用回溯算法解决，比如数独、八皇后、0-1 背包、图的着色、旅行商问题、全排列等等。既然应用如此广泛，我们今天就来学习一下这个算法思想，看看它是如何指导我们解决问题的。

回溯的处理思想，有点类似枚举搜索。我们枚举所有的解，找到满足期望的解。为了有规律地枚举所有可能的解，避免遗漏和重复，我们把问题求解的过程分为多个阶段。每个阶段，我们都会面对一个岔路口，我们先随意选一条路走，当发现这条路走不通的时候（不符合期望的解），就回退到上一个岔路口，另选一种走法继续走。

八皇后问题

我们有一个 8x8 的棋盘，希望往里放 8 个棋子（皇后），每个棋子所在的行、列、对角线都不能有另一个棋子。你可以看我画的图，第一幅图是满足条件的一种方法，第二幅图是不满足条件的。八皇后问题就是期望找到所有满足这种要求的放棋子方式。

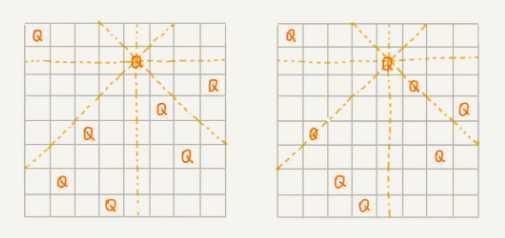
 我们把这个问题划分成 8 个阶段，依次将 8 个棋子放到第一行、第二行、第三行……第八行。在放置的过程中，我们不停地检查当前的方法，是否满足要求。如果满足，则跳到下一行继续放置棋子；如果不满足，那就再换一种方法，继续尝试。

分析一下，八皇后就是从0-8行，分析每个棋子的特性。

　　1.我们保证的是每行只有一个棋子，所以横向的无交叉棋子满足了

　　2.我们从上往下排列棋子，保证同col上，当前要摆放棋子的行往上都没有交叉棋子。

　　3.对角线这个看图就很明显了，就是保证当前要摆放棋子的位置，上面的行的col - 1， col + 1没有棋子，这边要“递归的遍历每行的”。

这个算法的特点在于只要某一处出了问题，它会将之前的也推倒重来，回溯就是这个思想。

其实还是看问题的分析，实际八皇后用回溯实现没有难度

int[] result = new int[8];//全局或成员变量,下标表示行,值表示queen存储在哪一列
public void cal8queens(int row) { // 调用方式：cal8queens(0);
  if (row == 8) { // 8个棋子都放置好了，打印结果
    printQueens(result);
    return; // 8行棋子都放好了，已经没法再往下递归了，所以就return
  }
  for (int column = 0; column < 8; ++column) { // 每一行都有8中放法
    if (isOk(row, column)) { // 有些放法不满足要求
      result[row] = column; // 第row行的棋子放到了column列
      cal8queens(row+1); // 考察下一行
    }
  }
}

private boolean isOk(int row, int column) {//判断row行column列放置是否合适
  int leftup = column - 1, rightup = column + 1;
  for (int i = row-1; i >= 0; --i) { // 逐行往上考察每一行
    if (result[i] == column) return false; // 第i行的column列有棋子吗？
    if (leftup >= 0) { // 考察左上对角线：第i行leftup列有棋子吗？
      if (result[i] == leftup) return false;
    }
    if (rightup < 8) { // 考察右上对角线：第i行rightup列有棋子吗？
      if (result[i] == rightup) return false;
    }
    --leftup; ++rightup;
  }
  return true;
}

private void printQueens(int[] result) { // 打印出一个二维矩阵
  for (int row = 0; row < 8; ++row) {
    for (int column = 0; column < 8; ++column) {
      if (result[row] == column) System.out.print("Q ");
      else System.out.print("* ");
    }
    System.out.println();
  }
  System.out.println();
}

回溯算法

标签：解答   https   规律   hellip   result   img   其它   拓展   计算   

原文地址：https://www.cnblogs.com/CherryTab/p/12093280.html