标签:马走日 操作 数据结构 总结 变量 || 元素 方法 解决
八皇后问题,是一个古老而著名的问题,问题如下:
在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
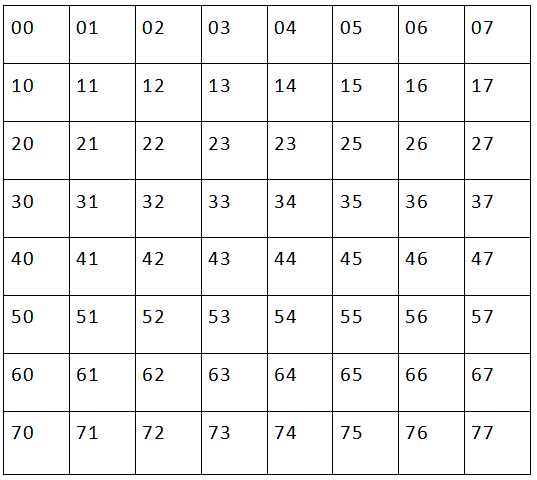
上边是一个8*8的国际棋盘,可以看到棋盘中的每个格子都标有数字。每个数字都是两位,十位数字表示该格子所在的行,而个位数字表示该格子所在的列。
这样不难发现,处在同一行的两个格子其十位数都相同,处在同一列的两个格子其个位数都相同,处在同一斜线的两个格子有:|两个数字个位数的差|=|两个数字十位数的差|。
主要的三个限制条件明白了,接下来我们选择一种数据结构对“皇后”进行存储。很明显,我们可以选择二维数组。但是还可以选择一维数组。在这里我们选择一维数组。
为什么选择一维数组呢?
1.因为一行只放一个皇后,很符合我们一维数组的存放特性,即一个索引对应一个元素。
2.相对于二维数组,一位数组比较简单,更适合初学者。
我们以皇后所在的行标作为一位数组的索引,皇后所在的列标作为该索引对应的元素,例如arr[3]=5,代表第三行的皇后在第五列。
下边我们以python以及JAVA为例来解决这个问题。
num=0 def eight_queen(arr,finish_line=0): if finish_line == len(arr): #如果放置皇后成功的行数与数组中的元素个数一致(即棋盘的行数)则认为完成了一种摆法 global num #将上边定义的num定义为全局变量 这样才能在后边对其进行自加操作 num+=1 print("第%s种摆法:" % num) for i in range(8): print((i,arr[i])) return # break for stand in range(len(arr)): #对整个列进行扫描,将列标的标号赋值给数组中对应的元素 arr[finish_line] = stand flag = True for line in range(finish_line): if arr[line] == stand or abs(arr[line]-stand) == finish_line-line: #有皇后与当前放置的皇后处于同一列或同一斜线上 flag = False # stand-=1 if flag==True: eight_queen(arr,finish_line+1) if __name__ == ‘__main__‘: eight_queen([None]*8) if num != 0: print("一共有%s种摆法" % num) else: print("无解")
对于初学者理解可能不是特别轻松,所以在这里我们总结一个的定式,再遇到此类问题时直接套用以下定式即可。下边再讲的相关问题我们就套用以下定式。
num=0 #全局变量代表方法的数量 def model(arr,finish_row=0): if finish_row == len(arr): #完成了一种方法 global num num+=1 return for x in range(循环边界): 具体操作 #对列表的需求操作 flag = True for y in range(循环边界): #找不符合条件的要求 if 找不符合要求的情况: flag = False if flag==True: #完成了一行摆放后递归调用 model(arr,finish_row+1) if __name__ == ‘__main__‘: model() #调用即可 print(num) #输出方法数
我们再把它改写为JAVA版:
public class eigthqueen { public static int num =0; //定义全局变量,表示摆法 public static void main(String[] args) { int [] arr = new int[8]; //以八皇后为例,定义对应长度的列表 int finish_row = 0; //初始完成的行数 equeen(arr,finish_row); System.out.println(); System.out.printf("一共%d种摆法",num); } static void equeen(int arr[],int finish_row){ boolean flag = true; if(finish_row==arr.length){ num++; System.out.println(); //初学java,比较笨的输出方式 System.out.printf("第%d种摆法",num); System.out.println(); for(int i=0;i<arr.length;i++){ System.out.print("("); System.out.print(i); System.out.print(","); System.out.print(arr[i]); System.out.print(")"); } return; } for(int col=0;col<arr.length;col++){ arr[finish_row] = col; flag = true; for(int row=0;row<finish_row;row++){ if((arr[row]==col)||(Math.abs(arr[row]-col)==finish_row-row)){ //有皇后与当前放置的皇后在同一列或统一斜线的情况 flag = false; } } if(flag==true){ //完成一行皇后的放置 equeen(arr,finish_row+1); } } } }
同样在JAVA中我们同样也可以总结定式:
public class eigthqueen { public static int num =0; //定义全局变量,表示摆法 public static void main(String[] args) { int [] arr = new int[8]; //以八皇后为例,定义对应长度的列表 int finish_row = 0; //初始完成的行数 equeen(arr,finish_row); System.out.printf("一共%d种摆法",num); } static void equeen(int arr[],int finish_row){ boolean flag = true; if(finish_row==arr.length){ num++; return; } for(int col=0;col<arr.length;col++){ 具体操作 //对列表的需求操作 flag = true; for(int row=0;row<finish_row;row++){ if(找不符合要求的情况){ flag = false; } } if(flag==true){ //完成一小步骤方法后递归 equeen(arr,finish_row+1); } } } }
接下来几篇我们要讲的马走日问题以及剪邮票等问题都可以套用这个定式来解决,这样就可以更加熟悉对这个定式的使用。
标签:马走日 操作 数据结构 总结 变量 || 元素 方法 解决
原文地址:https://www.cnblogs.com/daimaxiaocai/p/11912271.html