标签:传参 解决 组合 ++ 数组 png 分治 main space
一.前提知识(分治思想)
将原问题分解为几个规模较小但类似与原问题的子问题,递归的求解这些子问题,然后再合并这些子问题的解来建立原问题的解。
分治模式在每层递归时都有三个步骤:
1.分解原问题为若干子问题,这些子问题是原问题的规模较小的实例。
2.解决这些子问题,递归地求解各子问题。当子问题的规模足够小的时候,则直接求解。
3.合并这些子问题的解成原问题的解。
二.归并排序算法
思想:分治的思想。
归并的步骤包括拆分和合并,其中合并是主要的步骤。
1.拆分过程
例如我们要排序的数组是
int a[]={3,2,4,7,6};
首先将上面的数组拆分成
int b[] = {3,2}; int c[] = {4,7,6};
然后再拆分成
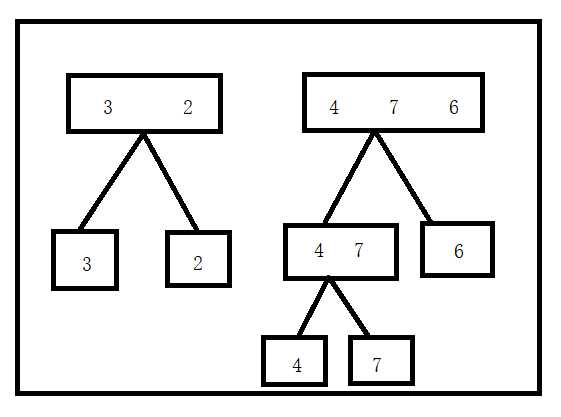
拆分到不能拆分(只有一个数)时。就可以合并。
2.合并过程
就是将最小子问题解决,比如先排序4,7。
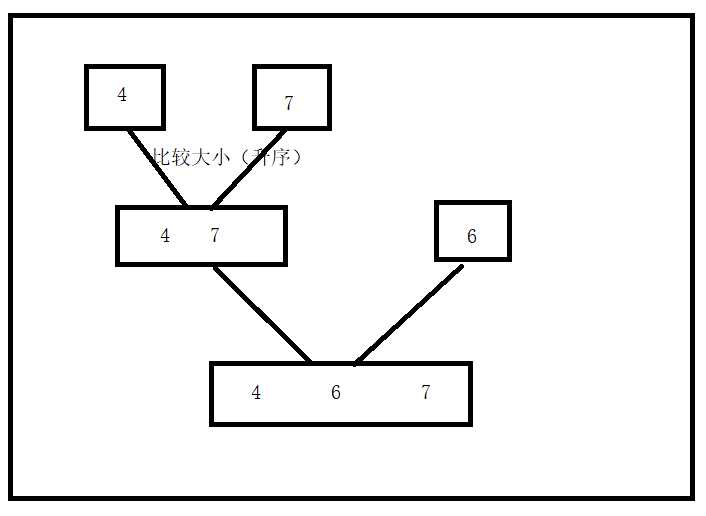
三.源码
#include<iostream> using namespace std; //合并 void Merge(int *a,int p,int q,int r){ //参数说明 a排序数组 p,q,r为下标且p<q<r int n1 = q-p+1; int n2 = r-q; int *L = new int[n1+1]; int *R = new int[n2+1]; int i,j,k; //获取此时的子数组 for(i=0;i<n1;i++){ L[i] = a[p+i]; } for(j=0;j<n2;j++){ R[j] = a[q+j+1]; } //将排好序的子数组合并到原数组 L[n1] = 1000000; R[n2] = 1000000; for(i=0,j=0,k=p;k<=r;k++){ if(L[i]<=R[j]){ a[k] = L[i]; i++; }else{ a[k] = R[j]; j++; } } delete []L; delete []R; } //拆分 void MergeSort(int *a,int p,int r){ //参数 a为待排序数组,p为排序的下标,r为排序的上标,p<r if(p<r){ int q = (p+r)/2; //将一个数组拆分成两个数组 MergeSort(a,p,q); MergeSort(a,q+1,r); //合并操作 Merge(a,p,q,r); } } int main() { // p q r为数组下标 int a[10] = {12,10,8,5,6,76,32,45,43,89}; MergeSort(a,0,3); //传参表示从a[0]到a[3]排序 for(int i =0;i<10;i++) { cout<<a[i]<<" "; } return 0; }
四.归并排序是时间复杂度稳定的排序算法,最差和最优都是O(nlogn)
标签:传参 解决 组合 ++ 数组 png 分治 main space
原文地址:https://www.cnblogs.com/zhang1568234/p/12114308.html