归并排序

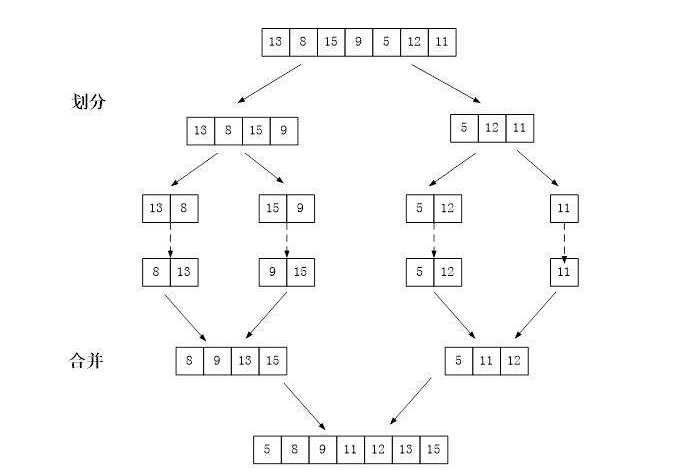
import java.util.Arrays;

public class MergeSort {

    public static void main(String[] args) {
        int arr[] = {8, 4, 5, 7, 1, 3, 6, 2};
        int temp[] = new int[arr.length];
        mergeSort(arr, 0, arr.length - 1, temp);
        System.out.println(Arrays.toString(arr));
    }

    public static void mergeSort(int[] arr, int left, int right, int[] temp) {
        if (left < right) {
            int mid = (left + right) / 2;
            mergeSort(arr, left, mid, temp);
            mergeSort(arr, mid + 1, right, temp);
            merge(arr,left,mid,right,temp);
        }
    }

    public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
        int i = left;
        int j = mid + 1;
        int t = 0;
        while (i <= mid && j <= right) {
            if (arr[i] < arr[j]) {
                temp[t] = arr[i];
                t++;
                i++;
            } else {
                temp[t] = arr[j];
                t++;
                j++;
            }
        }
        while (i <= mid) {
            temp[t] = arr[i];
            t++;
            i++;
        }
        while (j <= right) {
            temp[t] = arr[j];
            t++;
            j++;
        }
        t = 0;
        int tempLeft = left;
        System.out.println(tempLeft+"---"+right);
        while (tempLeft <= right) {
            arr[tempLeft] = temp[t];
            t++;
            tempLeft++;
        }
    }
}