标签:出现 结构 多项式 cloc 两种方法 相同 src 正整数 数量级
1、用for循环写一个函数,实现从1开始输出到N的正整数。
有两宗实现方法,一种是递归,另一种是非递归
//非递归 void PrintN1(int N){ int i; for(i=1;i<=N;i++){ printf("%d\n",i); } return; }
//递归 递归对空间的需求很大,当数字很大的时候,需要很大的内存,当数字是十万的时候递归就崩了 void PrintN2(int N){ if(N){ PrintN2(N-1); printf("%d\n",N); } return; }
这里都能实现功能,但递归的缺点就是占用内存很严重,递归能更好的理解程序,但他的缺点却让很多程序员诟病,所以用递归的时候要考虑递归是否会出现内存溢出的问题
这个问题也让我想到了重庆邮电大学的数据结构初试大题,好像是2018年的题还是19的题,他的题目就是用递归实现的,问这个程序的缺点在哪里,并指出改正,好想是这样的,所以学到的东西到处都在用到啊,以前肯定也是学过这个,但我做那题的时候就是没有想到内存溢出问题。
2,、多项式的计算问题

这里计算多项式,方法有两种,第一种肯定也是我们大家常常会想到的方法,但这种方法缺是很不理想的方法。
上图的第一种方法就是直接计算,第二种方法是运用数学合并过后一项一项计算出来的,结果是第二种方法更省时间。
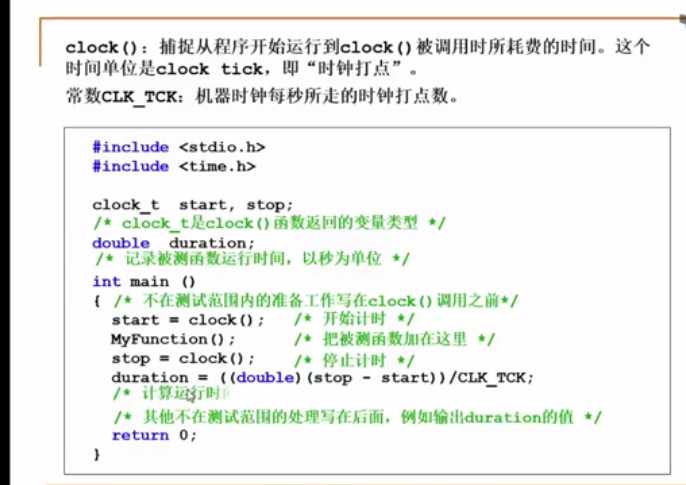
这里有又有一个在c语言中记录函数运行时间的方法。如下图
#include<stdio.h> #include<math.h> #include<time.h> clock_t start,stop; double duration; #define MAXN 100 //多项式最大项数 double f1(int n,double a[],double x) { int i; double p=a[0]; for(i=1; i<=n; i++) { p+=(a[i]*pow(x,i)); } return p; } double f2(int n,double a[],double x) { int i; double p=a[n]; for(i=n; i>0; i--) { p=a[i-1]+x*p; } return p; } int main() { int i; double a[MAXN];//存储多项式的系数 for(i=0; i<MAXN; i++) a[i]=(double)i;//给多项式赋值 //f1函数的测试 start = clock(); //开始计时 printf("f1=%f\n",f1(MAXN-1,a,1.1)); //中间为需要计时的函数 f1(MAXN-1,a,1.1); stop = clock(); //停止计时 duration=((double)(stop-start))/CLK_TCK; printf("ticks1 = %f\n",(double)(stop-start)); printf("duration1 = %6.2e\n",duration); //f1函数的测试 start = clock(); printf("f2=%6.2e",f2(MAXN-1,a,1.1)); f2(MAXN-1,a,1.1); stop = clock(); duration=((double)(stop-start))/CLK_TCK; printf("ticks2 = %f\n",(double)(stop-start)); printf("duration2 = %6.2e\n",duration); return 0; }
这是我自己跟着老师的视频打的,结果也真的是相差一个数量级。需要自己测试的话,就只需改MAXN就好了。
其中后面的代码有部分是相同的,合格的程序员肯定是要用的函数的,我们省事就直接那样写了,老师的原话,哈哈哈。
最后解决问题的时间复杂程度和解决问题的方法是有很大关系的。
标签:出现 结构 多项式 cloc 两种方法 相同 src 正整数 数量级
原文地址:https://www.cnblogs.com/simongreen/p/12136098.html