数据结构与算法简记--动态规划理论

标签：定义   image   pre   节点   简单   情况   抽象   oid   ==   

动态规划理论

一个模型三个特征

• 多阶段决策最优解模型
• 最优子结构
  • 最优子结构指的是，问题的最优解包含子问题的最优解。反过来说就是，我们可以通过子问题的最优解，推导出问题的最优解。
  • 如果我们把最优子结构，对应到我们前面定义的动态规划问题模型上，那我们也可以理解为，后面阶段的状态可以通过前面阶段的状态推导出来。
• 无后效性
  • 无后效性有两层含义，第一层含义是，在推导后面阶段的状态的时候，我们只关心前面阶段的状态值，不关心这个状态是怎么一步一步推导出来的。
  • 第二层含义是，某阶段状态一旦确定，就不受之后阶段的决策影响。无后效性是一个非常“宽松”的要求。只要满足前面提到的动态规划问题模型，其实基本上都会满足无后效性。
• 重复子问题
  • 这个概念比较好理解。前面一节，我已经多次提过。如果用一句话概括一下，那就是，不同的决策序列，到达某个相同的阶段时，可能会产生重复的状态。

结合例子理解理论

• 假设我们有一个 n 乘以 n 的矩阵 w[n][n]。矩阵存储的都是正整数。棋子起始位置在左上角，终止位置在右下角。我们将棋子从左上角移动到右下角。每次只能向右或者向下移动一位。从左上角到右下角，会有很多不同的路径可以走。我们把每条路径经过的数字加起来看作路径的长度。那从左上角移动到右下角的最短路径长度是多少呢？
• 
• 一个模型：
  • 从 (0, 0) 走到 (n-1, n-1)，总共要走 2*(n-1) 步，也就对应着 2*(n-1) 个阶段。
  • 每个阶段都有向右走或者向下走两种决策，并且每个阶段都会对应一个状态集合。
  • 我们把状态定义为 min_dist(i, j)，其中 i 表示行，j 表示列。min_dist 表达式的值表示从 (0, 0) 到达 (i, j) 的最短路径长度。所以，这个问题是一个多阶段决策最优解问题，符合动态规划的模型。
• 三个特征：
  • 画一下递归树会发现有重复的节点，表示从左上角到节点对应的位置，有多种路线，说明这个问题中存在重复子问题。
  • 计算 (i, j) 位置对应的状态，只需要关心 (i-1, j)，(i, j-1) 两个位置对应的状态，前面阶段的状态确定之后，不会被后面阶段的决策所改变，符合“无后效性”。
  • 把从起始位置 (0, 0) 到 (i, j) 的最小路径，记作 min_dist(i, j)，min_dist(i, j) 可以通过 min_dist(i, j-1) 和 min_dist(i-1, j) 两个状态推导出来，符合“最优子结构”。

两种动态规划解题思路总结

1. 状态转移表法解题思路大致可以概括为，回溯算法实现 - 定义状态 - 画递归树 - 找重复子问题 - 画状态转移表 - 根据递推关系填表 - 将填表过程翻译成代码。
2. 状态转移方程法的大致思路可以概括为，找最优子结构 - 写状态转移方程 - 将状态转移方程翻译成代码。

• 状态转移表法
  • 先使用回溯算法的暴力搜索解决，画出递归树，判断是否存在重复子问题，找出规律看是否可用动态规划解决。
  • 如果存在，两种解决方法：
    • 使用回溯+备忘录解决重复节点
    • 状态转移表法：
      • 先画出一个状态表。状态表一般都是二维的，所以你可以把它想象成二维数组。
      • 其中，每个状态包含三个变量，行、列、数组值。我们根据决策的先后过程，从前往后，根据递推关系，分阶段填充状态表中的每个状态。最后，我们将这个递推填表的过程，翻译成代码，就是动态规划代码了。
• 应用：解决上面最短路径问题
  • 先回溯算法穷举

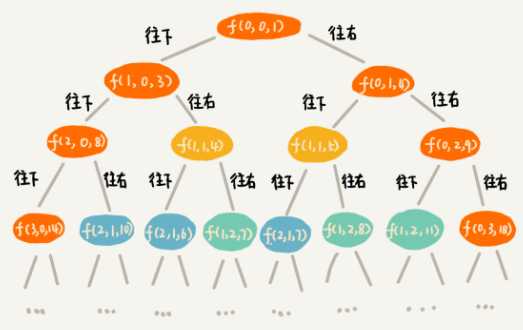
  • private int minDist = Integer.MAX_VALUE; // 全局变量或者成员变量
    // 调用方式：minDistBacktracing(0, 0, 0, w, n);
    public void minDistBT(int i, int j, int dist, int[][] w, int n) {
      // 到达了n-1, n-1这个位置了，这里看着有点奇怪哈，你自己举个例子看下
      if (i == n && j == n) {
        if (dist < minDist) minDist = dist;
        return;
      }
      if (i < n) { // 往下走，更新i=i+1, j=j
        minDistBT(i + 1, j, dist+w[i][j], w, n);
      }
      if (j < n) { // 往右走，更新i=i, j=j+1
        minDistBT(i, j+1, dist+w[i][j], w, n);
      }
    }

     

  • 画出递归树，以此来寻找重复子问题， (i, j) 重复的节点，我们只需要选择 dist 最小的节点，继续递归求解，其他节点就可以舍弃了
  • 

  •  

    画出一个二维状态表 

  • 

  •  

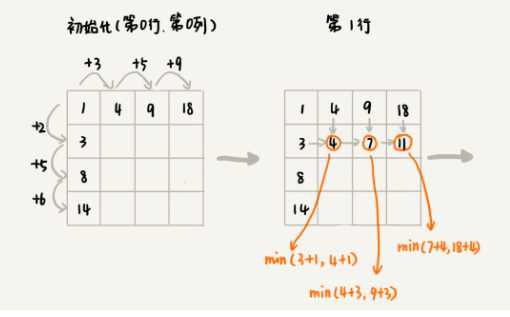
    public int minDistDP(int[][] matrix, int n) {
      int[][] states = new int[n][n];
      int sum = 0;
      for (int j = 0; j < n; ++j) { // 初始化states的第一行数据
        sum += matrix[0][j];
        states[0][j] = sum;
      }
      sum = 0;
      for (int i = 0; i < n; ++i) { // 初始化states的第一列数据
        sum += matrix[i][0];
        states[i][0] = sum;
      }
      for (int i = 1; i < n; ++i) {
        for (int j = 1; j < n; ++j) {
          states[i][j] = 
                matrix[i][j] + Math.min(states[i][j-1], states[i-1][j]);
        }
      }
      return states[n-1][n-1];
    }

• 状态转移方程法

  • 类似递归的解题思路。我们需要分析，某个问题如何通过子问题来递归求解，也就是所谓的最优子结构。

  • 根据最优子结构，写出递归公式，也就是所谓的状态转移方程。有了状态转移方程，代码实现就非常简单了。

  • 一般情况下，我们有两种代码实现方法，一种是递归加“备忘录”，另一种是迭代递推。

  • 强调：状态转移方程是解决动态规划的关键，写出状态转移方程，问题就解决了一半！！

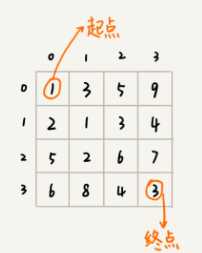
  • 应用：解决上面的最短路径问题

    • 状态转移方程：

      min_dist(i, j) = w[i][j] + min(min_dist(i, j-1), min_dist(i-1, j))

    • 实现代码

    • private int[][] matrix = 
               {{1，3，5，9}, {2，1，3，4}，{5，2，6，7}，{6，8，4，3}};
      private int n = 4;
      private int[][] mem = new int[4][4];
      public int minDist(int i, int j) { // 调用minDist(n-1, n-1);
        if (i == 0 && j == 0) return matrix[0][0];
        if (mem[i][j] > 0) return mem[i][j];
        int minLeft = Integer.MAX_VALUE;
        if (j-1 >= 0) {
          minLeft = minDist(i, j-1);
        }
        int minUp = Integer.MAX_VALUE;
        if (i-1 >= 0) {
          minUp = minDist(i-1, j);
        }
        
        int currMinDist = matrix[i][j] + Math.min(minLeft, minUp);
        mem[i][j] = currMinDist;
        return currMinDist;
      }

       

四种算法思想比较分析

• 分类
  • 贪心、回溯、动态规划：解决多阶段决策最优解模型。
  • 分治：解决的问题尽管大部分也是最优解问题，但是，大部分都不能抽象成多阶段决策模型
• 回溯算法：
  • 相当于穷举搜索，“万金油”，基本上能用的动态规划、贪心解决的问题，我们都可以用回溯算法解决。
  • 时间复杂度高：指数级
• 动态规划：
  • 动态规划比回溯算法高效。
  • 需要满足一个模型三个特征。
  • 动态规划和分治算法在重复子问题上区分非常明显。分治算法要求分割成的子问题，不能有重复子问题，而动态规划正好相反，动态规划之所以高效，就是因为回溯算法实现中存在大量的重复子问题。
• 贪心算法
  • 动态规划算法的一种特殊情况。
  • 更加高效，代码实现也更加简洁。
  • 可以解决的问题也更加有限。它能解决的问题需要满足三个条件，最优子结构、无后效性和贪心选择性（这里我们不怎么强调重复子问题）。
  • 贪心选择性”的意思是，通过局部最优的选择，能产生全局的最优选择。

数据结构与算法简记--动态规划理论

标签：定义   image   pre   节点   简单   情况   抽象   oid   ==   

原文地址：https://www.cnblogs.com/wod-Y/p/12146673.html