标签:垂直 方式 atp 索引 结果 lang pre 金融 bar
大家都知道,Matplotlib 是众多 Python 可视化包的鼻祖,也是Python最常用的标准可视化库,其功能非常强大,同时也非常复杂,想要搞明白并非易事。但自从Python进入3.0时代以后,pandas的使用变得更加普及,它的身影经常见于市场分析、爬虫、金融分析以及科学计算中。
作为数据分析工具的集大成者,pandas作者曾说,pandas中的可视化功能比plt更加简便和功能强大。实际上,如果是对图表细节有极高要求,那么建议大家使用matplotlib通过底层图表模块进行编码。当然,我们大部分人在工作中是不会有这样变态的要求的,所以一句import pandas as pd就足够应付全部的可视化工作了。下面,我们总结一下PD库的一些使用方法和入门技巧。
一、线型图
对于pandas的内置数据类型,Series 和 DataFrame 都有一个用于生成各类 图表 的 plot 方法。 默认情况下, 它们所生成的是线型图。其实Series和DataFrame上的这个功能只是使用matplotlib库的plot()方法的简单包装实现。
参考以下示例代码 :
import pandas as pd import numpy as np df = pd.DataFrame(np.random.randn(10,4),index=pd.date_range(‘2018/12/18‘, periods=10), columns=list(‘ABCD‘)) df.plot()
执行上面示例代码,得到以下结果 -
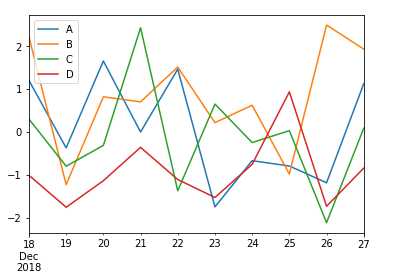
如果索引由日期组成,则调用gct().autofmt_xdate()来格式化x轴,如上图所示。
我们可以使用x和y关键字绘制一列与另一列。
s = Series( np. random. randn( 10). cumsum(), index= np. arange( 0, 100, 10))
s. plot()
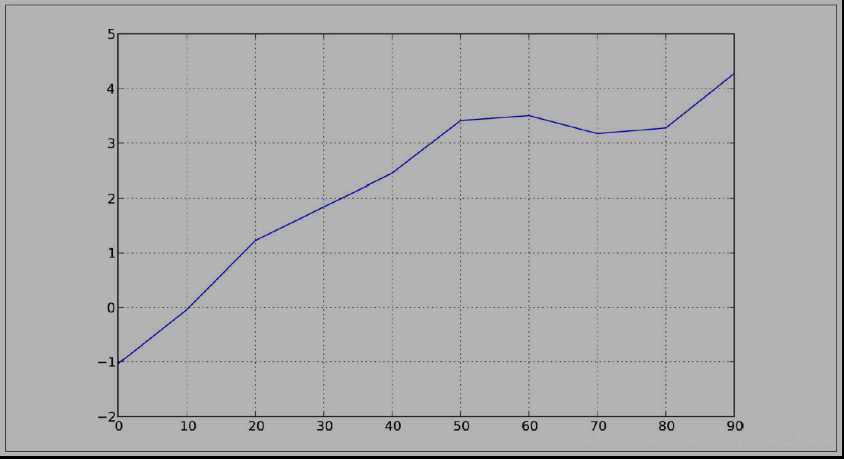
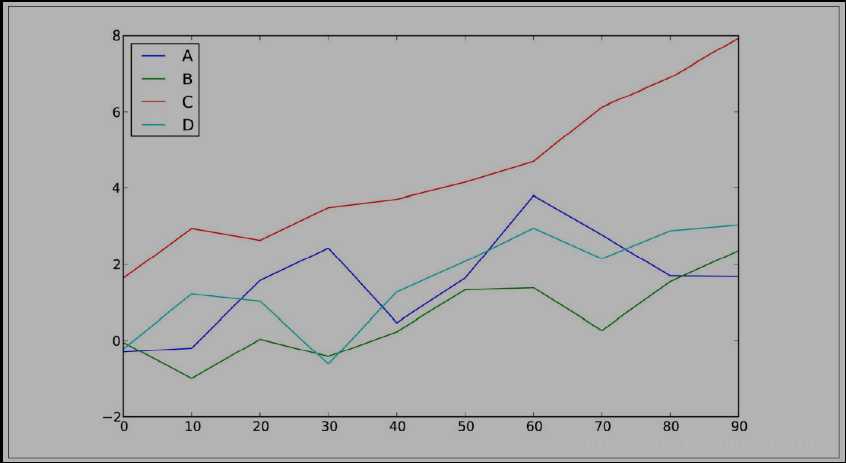
pandas 的大部分绘图方法都有 一个 可选的ax参数, 它可以是一个 matplotlib 的 subplot 对象。 这使你能够在网格 布局 中 更为灵活地处理 subplot 的位置。 DataFrame的plot 方法会在 一个 subplot 中为各列绘制 一条 线, 并自动创建图例( 如图所示):
df = DataFrame( np. random. randn( 10, 4). cumsum( 0), ...: columns=[‘ A‘, ‘B‘, ‘C‘, ‘D‘], index= np. arange( 0, 100, 10)) df. plot()
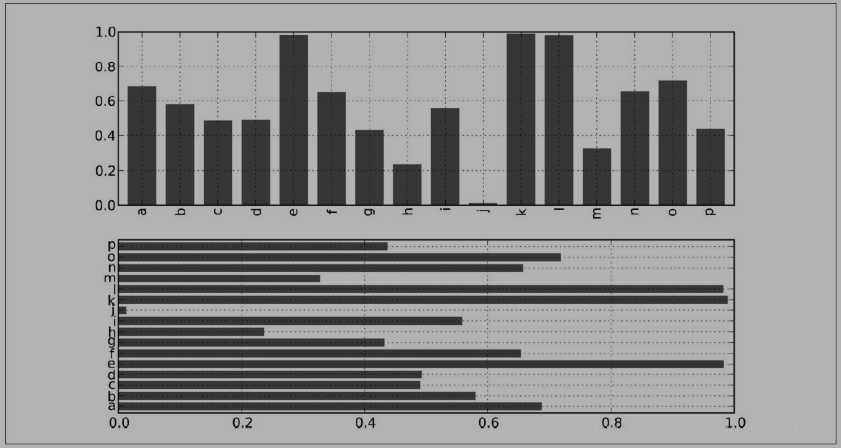
在生成线型图的代码中加上 kind=‘ bar‘( 垂直柱状图) 或 kind=‘ barh‘( 水平柱状图) 即可生成柱状图。 这时,Series 和 DataFrame 的索引将会被用 作 X( bar) 或 (barh)刻度:
In [59]: fig, axes = plt. subplots( 2, 1) In [60]: data = Series( np. random. rand( 16), index= list(‘ abcdefghijklmnop‘)) In [61]: data. plot( kind=‘ bar‘, ax= axes[ 0], color=‘ k‘, alpha= 0. 7) Out[ 61]: < matplotlib. axes. AxesSubplot at 0x4ee7750> In [62]: data. plot( kind=‘ barh‘, ax= axes[ 1], color=‘ k‘, alpha= 0.
对于 DataFrame, 柱状 图 会 将 每一 行的 值 分为 一组, 如图 8- 16 所示:
In [63]: df = DataFrame( np. random. rand( 6, 4), ...: index=[‘ one‘, ‘two‘, ‘three‘, ‘four‘, ‘five‘, ‘six‘], ...: columns= pd. Index([‘ A‘, ‘B‘, ‘C‘, ‘D‘], name=‘ Genus‘)) In [64]: df Out[ 64]: Genus A B C D one 0. 301686 0. 156333 0. 371943 0. 270731 two 0. 750589 0. 525587 0. 689429 0. 358974 three 0. 381504 0. 667707 0. 473772 0. 632528 four 0. 942408 0. 180186 0. 708284 0. 641783 five 0. 840278 0. 909589 0. 010041 0. 653207 six 0. 062854 0. 589813 0. 811318 0. 060217 In [65]: df. plot( kind=‘ bar‘)
现在通过创建一个条形图来看看条形图是什么。条形图可以通过以下方式来创建 -
import pandas as pd import numpy as np df = pd.DataFrame(np.random.rand(10,4),columns=[‘a‘,‘b‘,‘c‘,‘d‘]) df.plot.bar()
执行上面示例代码,得到以下结果 -
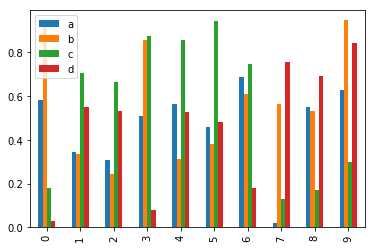
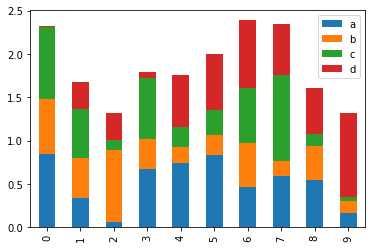
要生成一个堆积条形图,通过指定:pass stacked=True -
import pandas as pd df = pd.DataFrame(np.random.rand(10,4),columns=[‘a‘,‘b‘,‘c‘,‘d‘]) df.plot.bar(stacked=True)
执行上面示例代码,得到以下结果 -
要获得水平条形图,使用barh()方法 -
import pandas as pd import numpy as np df = pd.DataFrame(np.random.rand(10,4),columns=[‘a‘,‘b‘,‘c‘,‘d‘]) df.plot.barh(stacked=True)
可以使用plot.hist()方法绘制直方图。我们可以指定bins的数量值。
import pandas as pd import numpy as np df = pd.DataFrame({‘a‘:np.random.randn(1000)+1,‘b‘:np.random.randn(1000),‘c‘: np.random.randn(1000) - 1}, columns=[‘a‘, ‘b‘, ‘c‘]) df.plot.hist(bins=20)
执行上面示例代码,得到以下结果 -
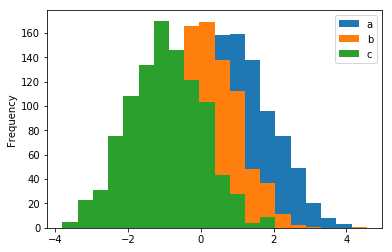
要为每列绘制不同的直方图,请使用以下代码 -
import pandas as pd import numpy as np df=pd.DataFrame({‘a‘:np.random.randn(1000)+1,‘b‘:np.random.randn(1000),‘c‘: np.random.randn(1000) - 1}, columns=[‘a‘, ‘b‘, ‘c‘]) df.hist(bins=20)
执行上面示例代码,得到以下结果 -
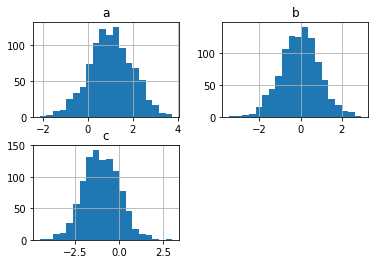
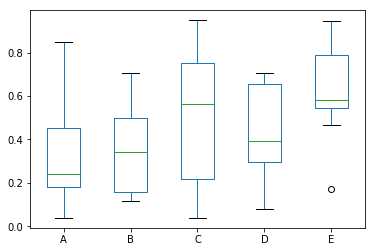
Boxplot可以绘制调用Series.box.plot()和DataFrame.box.plot()或DataFrame.boxplot()来可视化每列中值的分布。
例如,这里是一个箱形图,表示对[0,1)上的统一随机变量的10次观察的五次试验。
import pandas as pd import numpy as np df = pd.DataFrame(np.random.rand(10, 5), columns=[‘A‘, ‘B‘, ‘C‘, ‘D‘, ‘E‘]) df.plot.box()
执行上面示例代码,得到以下结果 -
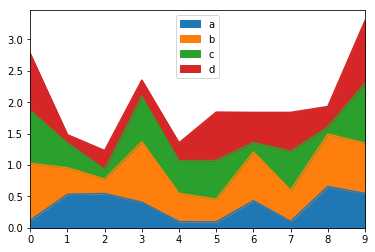
可以使用Series.plot.area()或DataFrame.plot.area()方法创建区域图形。
import pandas as pd import numpy as np df = pd.DataFrame(np.random.rand(10, 4), columns=[‘a‘, ‘b‘, ‘c‘, ‘d‘]) df.plot.area()
执行上面示例代码,得到以下结果 -
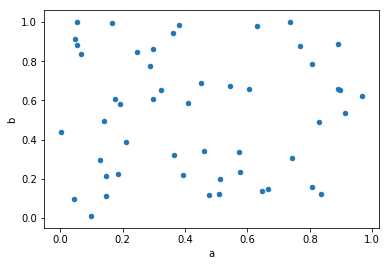
可以使用DataFrame.plot.scatter()方法创建散点图。
import pandas as pd import numpy as np df = pd.DataFrame(np.random.rand(50, 4), columns=[‘a‘, ‘b‘, ‘c‘, ‘d‘]) df.plot.scatter(x=‘a‘, y=‘b‘)
执行上面示例代码,得到以下结果 -
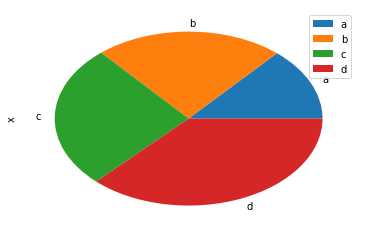
饼状图可以使用DataFrame.plot.pie()方法创建。
import pandas as pd import numpy as np df = pd.DataFrame(3 * np.random.rand(4), index=[‘a‘, ‘b‘, ‘c‘, ‘d‘], columns=[‘x‘]) df.plot.pie(subplots=True)
执行上面示例代码,得到以下结果 -
公众号python社区营
Python数据分析:手把手教你用Pandas生成可视化图表
标签:垂直 方式 atp 索引 结果 lang pre 金融 bar
原文地址:https://www.cnblogs.com/pypypy/p/12147163.html