标签:排序 ons ret printf The lse header ade 数组
\(S\):需要处理的字符串,长度为 \(len\)
\(suf_i\):字符串\(S\)中下标为 \(i \sim len\) 的连续子串(即后缀)
\(rank_i\):\(suf_i\)在所有后缀中的排名
\(SA_i\):后缀数组,排名为\(i\)的后缀在原串中的位置,满足 \(suf_{SA_1} < suf_{SA_2} < \dots < suf_{SA_{len}}\),与 \(rank_i\) 为互逆运算
\(height_i\):高度数组,排名相邻的两个后缀的最长公共前缀长度。
\[
height_i =
\begin{cases}
0, & i=0 \lcp(suf_{SA_i}, suf_{SA_{i-1}}), & i > 0
\end{cases}
\]
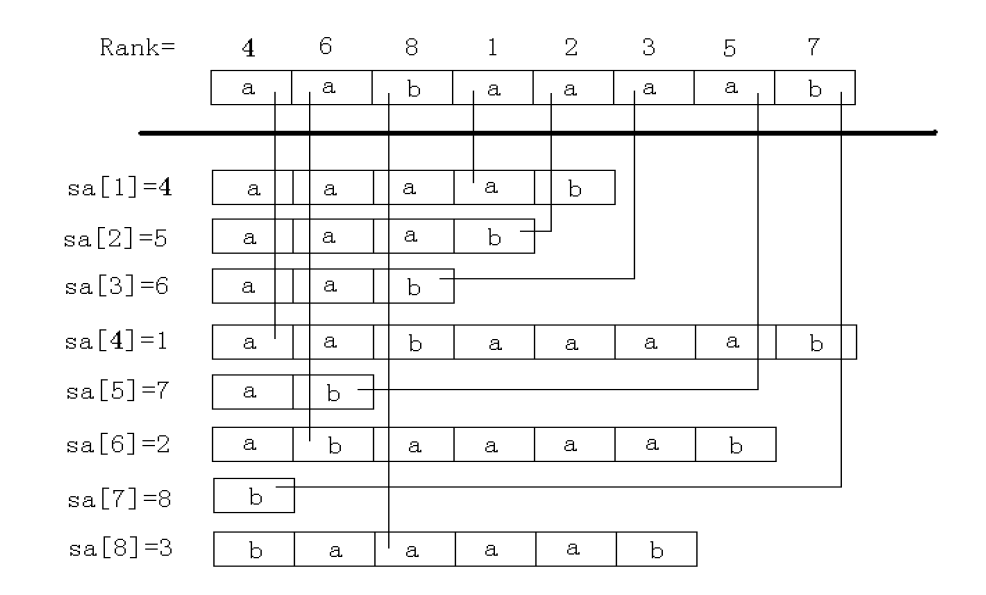
倍增算法的主要思路是,每次利用上一次的结果,倍增计算出每个位置从 \(i\) 开始的长度为 \(2^k\) 的子串的排名。
例如,在算法的开始,我们有 "aabaaaab" ,长度为 \(2^0=1\) 的子串的排名分别为:
| \(S_i\) | a | a | b | a | a | a | a | b |
|---|---|---|---|---|---|---|---|---|
| \(rank_i\) | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 2 |
然后,为了求出长度为 \(2^1=2\) 的子串的排名,我们以每个位置 \(i\) 开始,长度为 \(2^0=1\) 的子串的排名作为位置 \(i\) 的第一关键字,以每个位置 \(i\) 开始,长度为 \(2^0=1\) 的子串的排名作为位置 \(i\) 的第二关键字,进行双关键字排序。
接下来,以此类推即可。
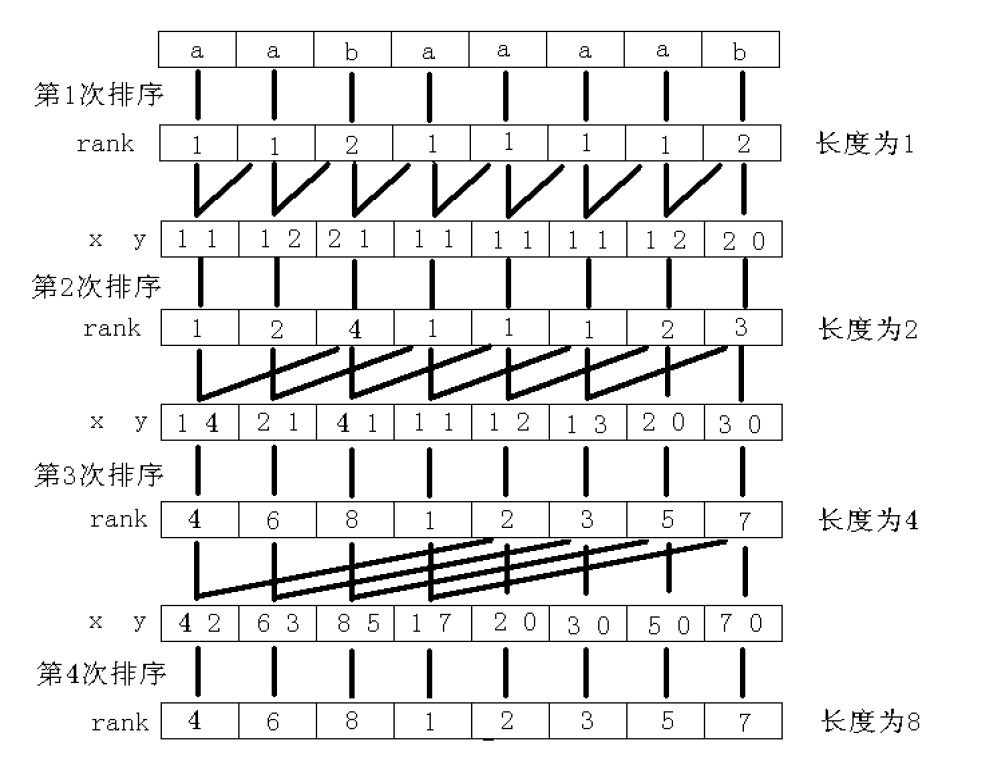
如果使用使用快速排序,那么复杂度将是 \(O(N\log^2 N)\) ,所以,我们在这里使用基数排序,复杂度将降为 \(O(N\log N)\)。
Code
inline void init() {
static int a[_], fir[_], sec[_], buc[_], tmp[_];
static char t[_];
copy(s + 1, s + N + 1, t + 1);
sort(t + 1, t + N + 1);
char *end = unique(t + 1, t + N + 1);
for (int i = 1; i <= N; ++i) a[i] = lower_bound(t + 1, end, s[i]) - t;
// 对每个字符单独排序,得到他们的排名
for (int i = 1; i <= N; ++i) ++buc[a[i]];
for (int i = 1; i <= N; ++i) buc[i] += buc[i - 1];
for (int i = 1; i <= N; ++i) rnk[i] = buc[a[i] - 1] + 1;
// 进行log n次迭代
for (int len = 1; len <= N; len <<= 1) {
// 设置每个位置的第一、第二关键字
for (int i = 1; i <= N; ++i) {
fir[i] = rnk[i];
sec[i] = i + len > N ? 0 : rnk[i + len];
}
// 对第二关键字进行排序,tmp[i]存储第i大的第二关键字的所在位置
fill(buc + 1, buc + N + 1, 0);
for (int i = 1; i <= N; ++i) ++buc[sec[i]];
for (int i = 1; i <= N; ++i) buc[i] += buc[i - 1];
for (int i = 1; i <= N; ++i) tmp[N - --buc[sec[i]]] = i;
// 对第一关键字进行排序,按照tmp中的顺序依次领取排名,在tmp中靠前的位置将较早领取排名,而较早领取到的排名较大
fill(buc + 1, buc + N + 1, 0);
for (int i = 1; i <= N; ++i) ++buc[fir[i]];
for (int i = 1; i <= N; ++i) buc[i] += buc[i - 1];
for (int i, j = 1; j <= N; ++j) {
i = tmp[j];
sa[buc[fir[i]]--] = i;
}
// 按照SA中的顺序求出名次数组rnk
bool uni = true;
for (int i, j = 1, last = 0; j <= N; ++j) {
i = sa[j];
if (!last)
rnk[i] = 1;
else if (fir[i] == fir[last] && sec[i] == sec[last])
rnk[i] = rnk[last], uni = false;
else
rnk[i] = rnk[last] + 1;
last = i;
}
if (uni) break;
}
}不会。
如果直接按照定义构造高度数组,那么时间复杂度是 \(O(N^2)\),难以承受,这就需要利用到高度数组的一个性质:
令 \(h_i\) 表示表示从第 \(i\) 个位置开始的后缀与排在其前一名的后缀的最长公共前缀,即当 \(rank_i>0\) 时
\[
h_i = lcp(suf_{i}, suf_{SA_{rank_{i}-1}})=height_{rank_i}
\]
对于 \(h_i\),有一个结论
\[
h_i \ge h_{i-1}-1
\]
证明(来自\(\mathrm{hihoCoder}\))
设 \(suf_k\) 是排在前 \(suf_{i-1}\)前 一名的后缀,
则它们的最长公共前缀是 \(h_{i-1}\)
那么将 \(suf_{k+1}\) 排在 \(suf_i\) 的前面
并且 \(suf_{k+1}\) 和 \(suf_i\) 的最长公共前缀是 \(h_{i-1}-1\) ,
所以 \(suf_i\) 和在它前一名的后缀的最长公共前缀至少是 \(h_{i-1}-1\)
Code
有了上面的性质,我们可以按照 \(height_{SA_i}\) 的顺序递推。 设 \(k=height_{rank_{i-1}}\) ,显然在计算每个 \(height_{rank_i}\) 时,\(k\) 每次减小\(1\) ,最多增加到 \(n\) ,所以这个过程的时间复杂度为 \(O(n)\)。
for (int i = 1, k = 0; i <= N; ++i) {
if (rnk[i] == 1)
k = 0;
else {
if (k > 0) --k;
int j = sa[rnk[i] - 1];
while (i + k <= N && j + k <= N && a[i + k] == a[j + k]) ++k;
}
height[rnk[i]] = k;
}通过高度数组 \(height_i\),我们可以得到排名相邻的两个后缀的最长公共前缀。
对于排名不相邻的两个后缀,它们的前缀的相似性比相邻后缀要差。显然排名不相邻的两个后缀的最长公共前缀长度一定不会比这两个后缀在后缀数组中确定的一段区间中任意两个相邻后缀的最长公共前缀长度更长。
所以,求出这段区间内最小的 \(height\) 值即为这两个不相邻后缀的最长公共前缀长度。
问题转化为 \(RMQ\) 问题,可以使用 \(ST\) 表解决。
#include <bits/stdc++.h>
using namespace std;
const int _ = 1e6 + 10;
int N, rnk[_], sa[_], height[_];
char s[_];
inline void init() {
static int a[_], fir[_], sec[_], buc[_], tmp[_];
static char t[_];
copy(s + 1, s + N + 1, t + 1);
sort(t + 1, t + N + 1);
char *end = unique(t + 1, t + N + 1);
for (int i = 1; i <= N; ++i) a[i] = lower_bound(t + 1, end, s[i]) - t;
// 对每个字符单独排序,得到他们的排名
for (int i = 1; i <= N; ++i) ++buc[a[i]];
for (int i = 1; i <= N; ++i) buc[i] += buc[i - 1];
for (int i = 1; i <= N; ++i) rnk[i] = buc[a[i] - 1] + 1;
// 进行log n次迭代
for (int len = 1; len <= N; len <<= 1) {
// 设置每个位置的第一、第二关键字
for (int i = 1; i <= N; ++i) {
fir[i] = rnk[i];
sec[i] = i + len > N ? 0 : rnk[i + len];
}
// 对第二关键字进行排序,tmp[i]存储第i大的第二关键字的所在位置
fill(buc + 1, buc + N + 1, 0);
for (int i = 1; i <= N; ++i) ++buc[sec[i]];
for (int i = 1; i <= N; ++i) buc[i] += buc[i - 1];
for (int i = 1; i <= N; ++i) tmp[N - --buc[sec[i]]] = i;
// 对第一关键字进行排序,按照tmp中的顺序依次领取排名,在tmp中靠前的位置将较早领取排名,而较早领取到的排名较大
fill(buc + 1, buc + N + 1, 0);
for (int i = 1; i <= N; ++i) ++buc[fir[i]];
for (int i = 1; i <= N; ++i) buc[i] += buc[i - 1];
for (int i, j = 1; j <= N; ++j) {
i = tmp[j];
sa[buc[fir[i]]--] = i;
}
// 按照SA中的顺序求出名次数组rnk
bool uni = true;
for (int i, j = 1, last = 0; j <= N; ++j) {
i = sa[j];
if (!last)
rnk[i] = 1;
else if (fir[i] == fir[last] && sec[i] == sec[last])
rnk[i] = rnk[last], uni = false;
else
rnk[i] = rnk[last] + 1;
last = i;
}
if (uni) break;
}
// for (int i = 1; i <= N; ++i) printf("%d ", sa[i]);
for (int i = 1, k = 0; i <= N; ++i) {
if (rnk[i] == 1)
k = 0;
else {
if (k > 0) --k;
int j = sa[rnk[i] - 1];
while (i + k <= N && j + k <= N && a[i + k] == a[j + k]) ++k;
}
height[rnk[i]] = k;
}
for (int i = 1; i <= N; ++i) printf("%d ", height[i]);
puts("");
}
int st[_][21], lg[21];
int main() {
#ifndef ONLINE_JUDGE
freopen("SA.in", "r", stdin);
freopen("SA.out", "w", stdout);
#endif
scanf("%s", s + 1);
N = strlen(s + 1);
init();
lg[0] = -1;
for (int i = 1; i <= N; ++i) st[i][0] = height[i], lg[i] = lg[i >> 1] + 1;
for (int j = 1; j <= 20; ++j)
for (int i = 1; i + (1 << j) - 1 <= N; ++i)
st[i][j] = min(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
int x, y;
scanf("%d%d", &x, &y);
x = rnk[x], y = rnk[y];
if (x > y) swap(x, y);
++x;
int mid = lg[y - x + 1];
printf("%d\n", max(st[x][mid], st[y - (1 << mid) + 1][mid]));
return 0;
}标签:排序 ons ret printf The lse header ade 数组
原文地址:https://www.cnblogs.com/newbielyx/p/12153654.html