半平面交算法及简单应用

时间：2014-11-01 21:38:39 阅读：229 评论：0 收藏：0 [点我收藏+]

标签：style blog http io color os ar for sp

半平面交算法及简单应用

半平面：一条直线把二维平面分成两个平面。

半平面交：在二维几何平面上，给出若干个半平面，求它们的公共部分

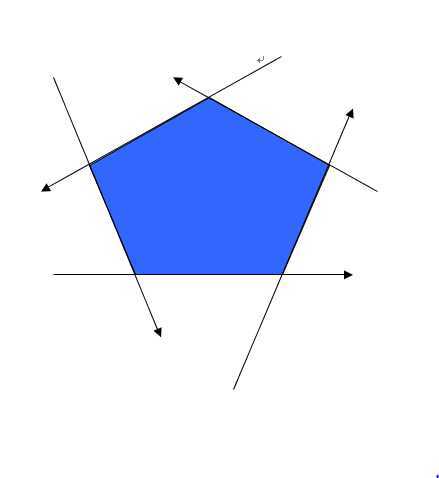
bubuko.com,布布扣

半平面交的结果：1.凸多边形（后面会讲解到）2.无界，因为有可能若干半平面没有形成封闭3.直线，线段，点，空（属于特殊情况吧）

算法：1：根据上图可以知道，运用给出的多边形每相邻两点形成一条直线来切割原有多边形，如果多边形上的点i在有向直线的左边或者在直线上即保存起来，否则判断此点的前一个点i-1和后一个点i+1是否在此直线的左边或线上，在的话分别用点i和点i-1构成的直线与此时正在切割的直线相交求出交点，这个交点显然也要算在切割后剩下的多边形里，同理点i和点i+1。原多边形有n条边，每条边都要进行切割，所以时间复杂度为O(n^2)。

2：第二种就是训练指南上面详细讲解的运用双端队列的半平面交算法，时间复杂度为O(nlogn)。仔细阅读代码应该能理解。

代码实现：以poj3130为例，裸的模板。

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<cstdlib>
 5 #include<cmath>
 6 #include<algorithm>
 7 #define inf 0x7fffffff
 8 #define exp 1e-10
 9 #define PI 3.141592654
10 using namespace std;
11 const int maxn=111;
12 struct Point
13 {
14     double x,y;
15     Point (double x=0,double y=0):x(x),y(y){}
16 }an[maxn],bn[maxn],cn[maxn];
17 ///an:记录最开始的多边形；bn:临时保存新切割的多边形；cn:保存新切割出的多边形
18 typedef Point Vector;
19 Vector operator + (Vector A,Vector B) {return Vector(A.x+B.x , A.y+B.y); }
20 Vector operator - (Vector A,Vector B) {return Vector(A.x-B.x , A.y-B.y); }
21 Vector operator * (Vector A,double p) {return Vector(A.x*p , A.y*p); }
22 Vector operator / (Vector A,double p) {return Vector(A.x/p , A.y/p); }
23 int dcmp(double x) {if (fabs(x)<exp) return 0;return x>0 ? 1 : -1;  }
24 double cross(Vector A,Vector B)
25 {
26     return A.x*B.y-B.x*A.y;
27 }
28 
29 double A,B,C;
30 int n,m;
31 void getline(Point a,Point b)///获取直线 Ax + By + C = 0
32 {
33     A=b.y-a.y;
34     B=a.x-b.x;
35     C=b.x*a.y-a.x*b.y;
36 }
37 ///getline()函数得到的直线和点a和点b所连直线的交点
38 Point intersect(Point a,Point b)
39 {
40     double u=fabs(A*a.x+B*a.y+C);
41     double v=fabs(A*b.x+B*b.y+C);
42     Point ans;
43     ans.x=(a.x*v+b.x*u)/(u+v);
44     ans.y=(a.y*v+b.y*u)/(u+v);
45     return ans;
46 }
47 void cut()///切割，原多边形的点为顺时针存储
48 {
49     int cnt=0;
50     for (int i=1 ;i<=m ;i++)
51     {
52         if (A*cn[i].x + B*cn[i].y + C>=0) bn[++cnt]=cn[i];
53         else
54         {
55             if (A*cn[i-1].x + B*cn[i-1].y + C > 0) bn[++cnt]=intersect(cn[i-1],cn[i]);
56             if (A*cn[i+1].x + B*cn[i+1].y + C > 0) bn[++cnt]=intersect(cn[i+1],cn[i]);
57         }
58     }
59     for (int i=1 ;i<=cnt ;i++) cn[i]=bn[i];
60     cn[0]=bn[cnt];
61     cn[cnt+1]=bn[1];
62     m=cnt;///新切割出的多边形的点数
63 }
64 void solve()
65 {
66     for (int i=1 ;i<=n ;i++) cn[i]=an[i];
67     an[n+1]=an[1];
68     cn[n+1]=an[1];
69     cn[0]=an[n];
70     m=n;
71     for (int i=1 ;i<=n ;i++)
72     {
73         getline(an[i],an[i+1]);
74         cut();
75     }
76 }
77 int main()
78 {
79     while (scanf("%d",&n)!=EOF && n)
80     {
81         for (int i=1 ;i<=n ;i++) scanf("%lf%lf",&an[i].x,&an[i].y);
82         reverse(an+1,an+n+1);
83         solve();
84         if (m) puts("1");
85         else puts("0");
86     }
87     return 0;
88 }

View Code

poj3335，给出两种方法

1.O(n^2)

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<cstdlib>
 5 #include<cmath>
 6 #include<algorithm>
 7 #define inf 0x7fffffff
 8 #define exp 1e-10
 9 #define PI 3.141592654
10 using namespace std;
11 const int maxn=111;
12 struct Point
13 {
14     double x,y;
15     Point (double x=0,double y=0):x(x),y(y){}
16 }an[maxn],bn[maxn],cn[maxn];
17 typedef Point Vector ;
18 Vector operator + (Vector A,Vector B) {return Vector(A.x+B.x , A.y+B.y); }
19 Vector operator - (Vector A,Vector B) {return Vector(A.x-B.x , A.y-B.y); }
20 Vector operator * (Vector A,double p) {return Vector(A.x*p , A.y*p); }
21 Vector operator / (Vector A,double p) {return Vector(A.x/p , A.y/p); }
22 int dcmp(double x) {if (fabs(x)<exp) return 0;return x>0 ? 1 : -1; }
23 double cross(Vector A,Vector B)
24 {
25     return A.x*B.y-B.x*A.y;
26 }
27 
28 int n,m;
29 double A,B,C;
30 void getline(Point a,Point b)
31 {
32     A=b.y-a.y;
33     B=a.x-b.x;
34     C=b.x*a.y-a.x*b.y;
35 }
36 Point intersect(Point a,Point b)
37 {
38     double u=fabs(A*a.x+B*a.y+C);
39     double v=fabs(A*b.x+B*b.y+C);
40     Point ans;
41     ans.x=(a.x*v+b.x*u)/(u+v);
42     ans.y=(a.y*v+b.y*u)/(u+v);
43     return ans;
44 }
45 void cut()
46 {
47     int cnt=0;
48     for (int i=1 ;i<=m ;i++)
49     {
50         if (A*cn[i].x+B*cn[i].y+C>=0)
51             bn[++cnt]=cn[i];
52         else
53         {
54             if (A*cn[i-1].x+B*cn[i-1].y+C>0)
55                 bn[++cnt]=intersect(cn[i-1],cn[i]);
56             if (A*cn[i+1].x+B*cn[i+1].y+C>0)
57                 bn[++cnt]=intersect(cn[i+1],cn[i]);
58         }
59     }
60     for (int i=1 ;i<=cnt ;i++) cn[i]=bn[i];
61     cn[0]=bn[cnt];
62     cn[cnt+1]=bn[1];
63     m=cnt;
64 }
65 void solve()
66 {
67     for (int i=1 ;i<=n ;i++) cn[i]=an[i];
68     an[n+1]=an[1];
69     cn[n+1]=cn[1];
70     cn[0]=cn[n];
71     m=n;
72     for (int i=1 ;i<=n ;i++)
73     {
74         getline(an[i],an[i+1]);
75         cut();
76     }
77 }
78 int main()
79 {
80     int t;
81     scanf("%d",&t);
82     while (t--)
83     {
84         scanf("%d",&n);
85         for (int i=1 ;i<=n ;i++) scanf("%lf%lf",&an[i].x,&an[i].y);
86         solve();
87         if (!m) printf("NO\n");
88         else printf("YES\n");
89     }
90     return 0;
91 }

View Code

2.O(nlogn)

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<cstring>
  4 #include<cstdlib>
  5 #include<cmath>
  6 #include<algorithm>
  7 #define inf 0x7fffffff
  8 #define exp 1e-10
  9 #define PI 3.141592654
 10 using namespace std;
 11 const int maxn=111;
 12 struct Point
 13 {
 14     double x,y;
 15     Point (double x=0,double y=0):x(x),y(y){}
 16 }an[maxn];
 17 typedef Point Vector;
 18 struct Line
 19 {
 20     Point p;
 21     Vector v;
 22     double ang;
 23     Line (){}
 24     Line (Point p,Vector v):p(p),v(v){ang=atan2(v.y,v.x); }
 25     //Line (Point p,Vector v):p(p),v(v) {ang=atan2(v.y,v.x); }
 26     friend bool operator < (Line a,Line b)
 27     {
 28         return a.ang<b.ang;
 29     }
 30 }bn[maxn];
 31 Vector operator + (Vector A,Vector B) {return Vector(A.x+B.x , A.y+B.y); }
 32 Vector operator - (Vector A,Vector B) {return Vector(A.x-B.x , A.y-B.y); }
 33 Vector operator * (Vector A,double p) {return Vector(A.x*p , A.y*p); }
 34 Vector operator / (Vector A,double p) {return Vector(A.x/p , A.y/p); }
 35 int dcmp(double x) {if (fabs(x)<exp) return 0;return x>0 ? 1 : -1; }
 36 double cross(Vector A,Vector B)
 37 {
 38     return A.x*B.y-B.x*A.y;
 39 }
 40 bool OnLeft(Line L,Point p)
 41 {
 42     return cross(L.v,p-L.p)>=0;///点P在有向直线L的左边（>=0说明在线上也算）
 43 }
 44 Point GetIntersection(Line a,Line b)
 45 {
 46     Vector u=a.p-b.p;
 47     double t=cross(b.v,u)/cross(a.v,b.v);
 48     return a.p+a.v*t;
 49 }
 50 //Point GetIntersection(Line l1, Line l2) {
 51 //    Point p;
 52 //    double dot1,dot2;
 53 //    //dot1 = multi(l2.a, l1.b, l1.a);
 54 //    dot1=cross(l1.b-l2.a , l1.a-l2.a);
 55 //    //dot2 = multi(l1.b, l2.b, l1.a);
 56 //    dot2=cross(l2.b-l1.b , l1.a-l1.b);
 57 //    p.x = (l2.a.x * dot2 + l2.b.x * dot1) / (dot2 + dot1);
 58 //    p.y = (l2.a.y * dot2 + l2.b.y * dot1) / (dot2 + dot1);
 59 //    return p;
 60 //}
 61 int HalfplaneIntersection(Line *L,int n,Point *poly)
 62 {
 63     sort(L,L+n);
 64 
 65     int first,last;
 66     Point *p=new Point[n];
 67     Line *q=new Line[n];
 68     q[first=last=0]=L[0];
 69     for (int i=1 ;i<n ;i++)
 70     {
 71         while (first<last && !OnLeft(L[i],p[last-1])) last--;
 72         while (first<last && !OnLeft(L[i],p[first])) first++;
 73         q[++last]=L[i];
 74         if (fabs(cross(q[last].v , q[last-1].v))<exp)
 75         {
 76             last--;
 77             if (OnLeft(q[last] , L[i].p)) q[last]=L[i];
 78         }
 79         if (first<last) p[last-1]=GetIntersection(q[last-1],q[last]);
 80     }
 81     while (first<last && !OnLeft(q[first],p[last-1])) last--;
 82     if (last-first<=1) return 0;
 83     p[last]=GetIntersection(q[last],q[first]);
 84     int m=0;
 85     for (int i=first ;i<=last ;i++) poly[m++]=p[i];
 86     return m;
 87 }
 88 void calPolygon(Point *p, int n, double &area, bool &shun)
 89 {
 90     p[n] = p[0];
 91     area = 0;
 92     double tmp;
 93     for (int i = 0; i < n; i++)
 94         area += p[i].x * p[i + 1].y - p[i].y * p[i + 1].x;
 95     area /= 2.0;
 96     if (shun = area < 0)
 97         area = -area;
 98 }
 99 bool calCore(Point *ps, int n)
100 {
101     Line l[maxn];
102     ps[n] = ps[0];
103     bool shun;
104     double area;
105     calPolygon(ps, n, area, shun);
106     if (shun)
107         for (int i = 0; i < n; i++)
108             bn[i] = Line(ps[i], ps[i] - ps[i + 1]);
109     else
110         for (int i = 0; i < n; i++)
111             bn[i] = Line(ps[i], ps[i + 1] - ps[i]);
112     Point pp[maxn];
113     return HalfplaneIntersection(bn, n, pp);
114 }
115 int main()
116 {
117     int t;
118     int n;
119     scanf("%d",&t);
120     while (t--)
121     {
122         scanf("%d",&n);
123         Point cn[maxn];
124         for (int i=0 ;i<n ;i++)
125         {
126             scanf("%lf%lf",&cn[i].x,&cn[i].y);
127         }
128 //        reverse(cn,cn+n);
129 //        for (int i=0 ;i<n ;i++)
130 //        {
131 //            bn[i].p=cn[i];
132 //            bn[i].v=cn[(i+1)%n]-cn[i];
133 //            bn[i].ang=atan2(bn[i].v.y , bn[i].v.x);
134 //        }
135 //        int m=HalfplaneIntersection(bn,n,an);
136         if (!calCore(cn,n)) puts("NO");
137         else puts("YES");
138     }
139     return 0;
140 }