标签:大于 else 直接插入排序 快速排序 swap ash auto http 额外
题目3
在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的,但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如,如果输入长度为7的数组{2,3,1,0,2,5,3},那么对应的输出是第一个重复的数字2。
解析
1.哈希表。用一个哈希表来从头到尾对数据进行扫描,扫描时通过O(1)时间对哈希表里是否包含某个数字来做判断,时间复杂度为O(n)
2.排序。将输入的数组进行排序,然后找重复的数字,时间复杂度为O(nlogn)
3.不先排序,在比较时对数据进行重排。由于如果数组没有重复数字时,会出现数字i出现在第i位,从头到尾扫描数组中的每个数字,当扫描到下标为i的数字m时,比较整个数字是否等于i。若等于,则继续扫描下一位;若不等,则拿它和第m个数字进行比较是否相等。若是,则找到重复数字,若不是,则交换。此时由于每个数字最多只要交换两次就能找到属于它的位置,时间复杂度为O(n)。而所有的操作步骤都在输入数组上进行,不需要额外分配内存处理数组,因此空间复杂度为O(1)。即将每个数字都移动到其对应的坐标位置上,移动时如果对应位置已存在整个数字,则出现重复。
解法
import java.util.HashSet; public class chapter2 { public static void main(String[] args) { // TODO Auto-generated method stub int[] test3 = {1,2,3,2,1}; int[] dup = {0}; boolean isDup = duplicate3(test3, test3.length, dup); System.out.print(dup[0]); } private static void swap(int[] nums, int i, int j) { int t=nums[i]; nums[i]=nums[j]; nums[j]=t; } public void quicksort(int[] nums,int left, int right) { int i, j, temp, t; if(left>right) { return; } i=left; j=right; temp=nums[left]; while(i<j) { while(temp<=nums[j] && i<j) { j--; } while(temp>=nums[i] && i<j) { i++; } if(i<j) { t=nums[j]; nums[i]=nums[j]; nums[j]=t; } } nums[left]=nums[i]; nums[i]=temp; quicksort(nums, left, j-1); quicksort(nums, j+1, right); } public static boolean duplicate1(int[] nums, int len, int[] dup) { if(nums == null || len <=0) { return false; } HashSet<Integer> set = new HashSet<>(); for(int i = 0;i < len;i++) { if(set.contains(nums[i])) { dup[0] = nums[i]; } else { set.add(nums[i]); } } return false; } public static boolean duplicate3(int[] nums, int len, int[] duplication) { if(nums == null || len <=0) { return false; } for(int i = 0;i < len;i++) { while(nums[i]!=i) { if(nums[i]==nums[nums[i]]) { duplication[0]=nums[i]; return true; } swap(nums, i, nums[i]); } } return false; } }
扩展--排序算法
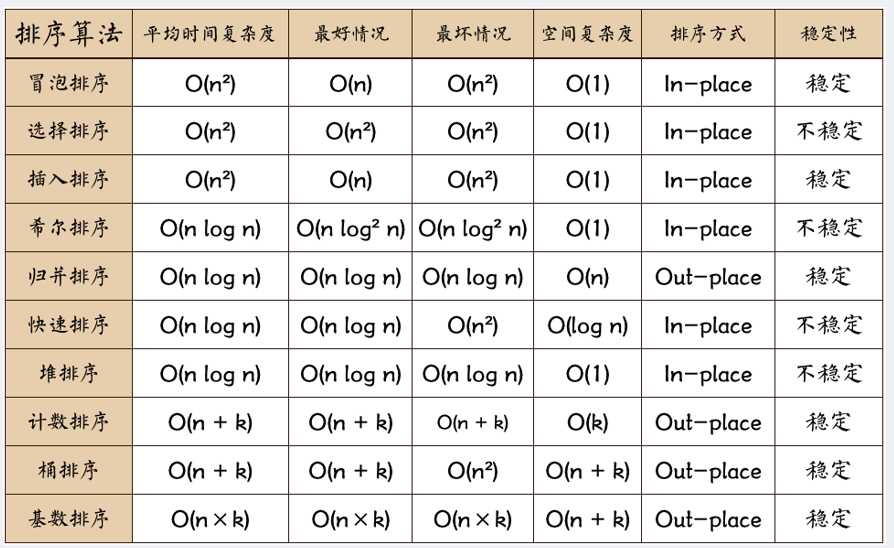
(图源于https://blog.csdn.net/weixin_41190227/article/details/86600821)
1.快速排序。挑选一个基准数,通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,即左边的数都比基准数小,右边的数都比基准数大。然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。平均情况下需要logn轮,因此快速排序算法的平均时间复杂度是O(nlogn)。
2.冒泡排序。重复地走访要排序的数列,一次比较两个元素,如果顺序错误就进行交换。不断比较相邻的元素,这样一轮下来,最后一个元素会是当前最大数。
3.选择排序。在未排序序列中找到最大/小元素,存放在排序序列的起始位置。然后不断从未排序的元素中寻找当前最大/小元素,放在已排序部分的末尾。
4.插入排序。通过构建有序序列,对于未排序的数据,在已排序序列中从后往前扫描,找到相应位置插入。
5.希尔排序。选择增量gap=length/2,缩小增量继续以gap = gap/2的方式,这种增量选择我们可以用一个序列来表示,{n/2,(n/2)/2…1},称为增量序列。按增量序列个数k,对序列进行k趟排序,每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1时,整个序列作为一个表来处理,表长度即为整个序列的长度。
6.归并排序。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。把长度为n的输入序列分成两个长度为n/2的子序列,对子序列分别采用归并排序。
7.堆排序。将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区。然后根据完全二叉树的排序,对堆进行有序排列。
8.计数排序。计数排序使用一个额外的数组C,用于统计待排序数组中每个元素出现的次数,其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。
9.桶排序。计数排序的升级版。假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序。
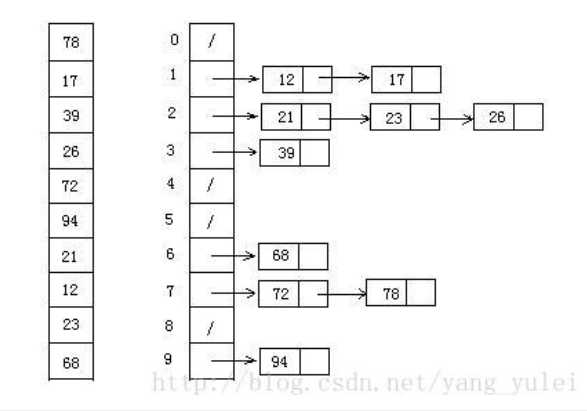
10.基数排序。 按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。基数排序基于分别排序,分别收集,所以是稳定的。
题目4
给定一个二维数组,其每一行从左到右递增排序,从上到下也是递增排序。给定一个数,判断这个数是否在该二维数组中。
解析
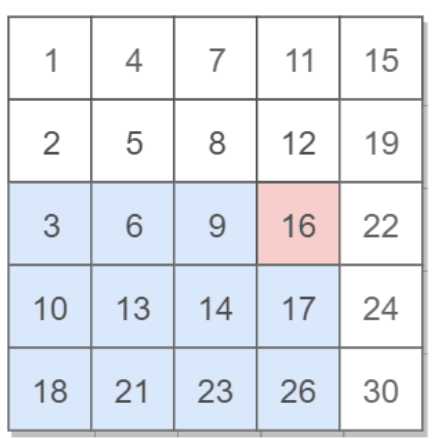
如图可知,若16为需要查找的数,那么小于16的数一定在其左边,大于16的数在其下方。那么从右上角开始进行查找,比较target和当前元素的大小关系来缩小区间。
1.如右上角元素为15,那么比较15<16,那么16不可能在15的同行,所以去掉第一行。
2.接着到了第二行,右上角元素为19,比较19>16,那么16不可能在19的同列,所以去掉最后一列。
3.接着再比较元素16,16=16,那么成功匹配。
此时时间复杂度为O(M+N),空间复杂度为O(1),M为行,N为列。
解法
public boolean findNum(int target, int[][] matrix) { if(matrix==null || matrix.length==0 || matrix[0].length==0) return false; int rows=matrix.length, cols=matrix[0].length; int r=0, c=cols-1; while(r<=rows-1 && c>=0) { if(target<matrix[r][c]) { c--; } else if(target>matrix[r][c]) { r++; } else return true; } return false; }
标签:大于 else 直接插入排序 快速排序 swap ash auto http 额外
原文地址:https://www.cnblogs.com/lyeeer/p/12188690.html