排序算法-线性时间复杂度

标签：次数   桶排序   编辑   大量   建立   运行时   ash   src   spl   

    一说到排序算法，大部分人都会说出著名的万金油-快速排序、大数据分而治之-归并排序、大数据排名-堆排序。这些排序无论在面试还是实际项目中，都是经常用到的一些排序算法，其平均时间复杂度都在 O(N • log_2^N)，那今天我们就来介绍几种 O(N)的排序算法。

    1，计数排序，输入 n 个范围在 0-k 区间的元素，当 !k >> n 时，排序的运行时间为 O(N)

          论点：对于输入的任一的元素 x，如果有 s 个元素小于，则元素 x 就可以放在 s+1 的位置上，这个时间复杂度近乎 O(1)，我们仅需要得出对于每个元素有多少个小于的元素的列表即可在很短的时间内排序完成。

          a.对原数组进行遍历，计算每个元素出现的次数，时间复杂度 O(N)，空间复杂度 O(K)

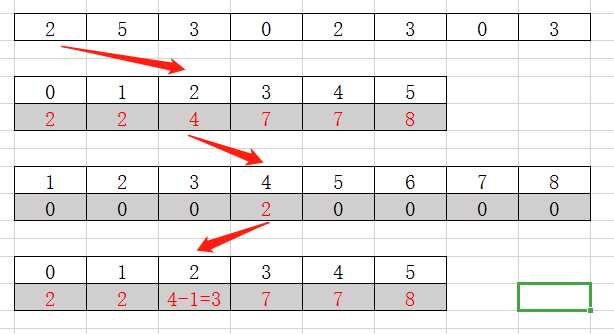
            原数组

 　　　　额外记录表，下标为元素，值代表出现的次数

         b,将记录的数组进行计算整理，数组中每个值代表小于当前下标的元素个数，时间复杂度O(K)

额外记录表，下标为元素，值代表小于当前下标的元素个数

         c.遍历原数组，并按最初提出的论点，进行最终的排序放置到最终数组，并更新记录表中的数值(v-1)，时间复杂度O(N) * O(1)，空间复杂度O(N)

         综上所述，所需要的时间复杂度为O(N) + O(K) + O(N)*O(1) = O(N + K)，当元素的取值范围较小时，可以达到 O(N)的时间复杂度，空间复杂度为O(N) + O(K) = O(N)

    2，基数排序，建立在计数排序（发现两种排序的谐音完全一样^_^）的基础上，所以请耐心阅读上一段的流程。

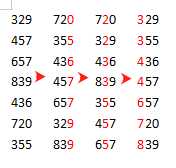
          论点：在实际项目过程中，我们需要排序的元素通常很难是在极小范围，这里我们可以利用位数的分隔，首先对所有数值的个位数进行计数排序，以此类推对十位、百位、千位。可以预见我们仅需要对当前元素组进行最大元素的位数次计数排序即可

                     假定最大元素为 x，则进行的计数排序个数为 r = ceil(ln(x)) 取上整数，每次计数排序的时间复杂度为 O(N + K) = O(N + 10) 整个算法复杂度为 ceil(ln(x)) * O(N + 10)，所以当最大一位的位数不会超过 ln(N)，则整个排序算法的复杂度为 常数 * O(N + 10) = O(N)，这种排序算法一般已经可以应用        　到很多项目场景中了，只是因为其编码的复杂度和现代计算机的 cpu 性能提高，所以除非巨量的数据排序，否则一般还是会采用快速排序

    3，桶排序，与基数排序是相反的思路，先生成 n 个相同大小的子区间（桶），将所有元素分到所属的桶内，并按插入排序的方式，放入所属的桶里，时刻保证每个桶内部的数据是有序的。

          论点：只要数据处于散列数据，可以预见每个桶的数据不会太多，除非极端情况下，但只要保证桶的个数，同样可以保证算法的线性时间复杂度（这里先不谈这种情况，这种已经类似于数值与数组下标逆向，需要消耗大量的空间）；

          a.生成 n 个桶，并设定每个桶的取值范围（可以去最大值后，向 n 倍数取上整，便于 hash 计算），时间复杂度 O(N)，空间复杂度O(N)，

          b.遍历整个数组，将元素放入所属桶，并根据插入排序保持桶的有序，时间复杂度 ∑^n-1_i=0（啊~！不会用这个数学符号编辑啊）O(ni²)，其中 n_i 表示每次插入排序时当前桶的数量。

          综上所述，时间复杂度的总时间为 O(N) + ... 上面的数学公式，以后学会怎么编辑再来修改。当数据服从均匀分布时，每次的插入排序期望值为 n*O(2-1/N)，验证较为复杂，有兴趣的同学可以参考算法导论.114页。

          可以得出时间复杂度为 O(N)

排序算法-线性时间复杂度

标签：次数   桶排序   编辑   大量   建立   运行时   ash   src   spl   

原文地址：https://www.cnblogs.com/novice-dxx/p/12198095.html