标签:算法 c中 使用 算法实现 ima 图像 idt 情况 默认

假设现在有一张500×400的图像,我们要通过缩放变换将它等比例缩放成一个400×320的图像。我们将原图像称为src,缩放后的图像称为dst,那么,对于dst上的所有像素点,我们都可以用src上的像素点来表示。最近临域插值算法通过反向变换得到一个浮点坐标,并对其进行简单取整,得到一个整型坐标。例如dst上的一个像素点(40,32),我们可以在src中找到对应的像素点(50,40)。因为像素点必须是整数,因此对于小数而言,我们需要取整,比如如果dst上的某个像素点对应到src上的像素点为(2.2,2.3),那么最近临域插值算法会自动取整,对应到src上的像素点就是(2.2)。也就是说,最近临域插值算法取的是浮点坐标最邻近的点对应的像素值。
因此,对于dst上的像素点(dst_X,dst_Y),我们可以通过src上的像素点(SrC_X,srC_Y)来进行计算:dst_X=srcX*(src_Height/dst_Height)dst_Y=srC_Y*(src_Width/dst_Width)
最近临域插值算法简单且直观,但由于它对浮点数的处理采用四舍五入的方法,直接取了和这个浮点数最接近的像素点的值,因此,通过最近临域插值算法缩放后的图像质量往往不高。
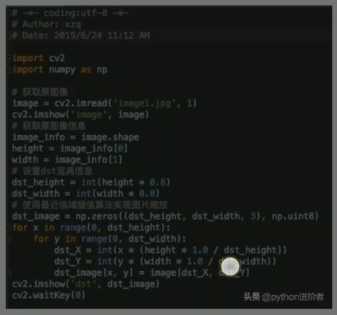
双线性插值算法是OpenCV默认使用的缩放算法,相比于最近临域插值算法对浮点数直接取整的处理,双线性插值算法则充分利用了这个浮点数像素点四周的四个像素点来共同决定最终的像素点。
我们还是假设dst上的某个像素点对应到src上的像素点为(2.2,2.3),双线性插值算法会首先对这个虚拟的浮点型像素点进行投影,可以是水平方向,也可以是竖直方向。
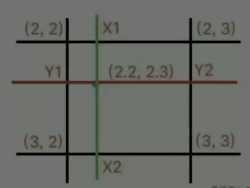
投影后分别在水平方向得到×1(2,2.3)、×2(3,2.3)两个点,在竖直方向得到Y1(2.2,2)、Y2(2.2,3)两个点。这四个点都是可以根据虚拟的浮点型像素点四周的四个实际像素点得到,然后我们可以根据X1、X2和Y1、Y2计算转化后的src像素点。我们以Y1、Y2为例,该浮点型像素点距Y1为0.2,距Y2为0.8,那么最终点就可以根据X1*30%+X2*70%和Y1*20%+Y2*80%确定。
双线性插值算法实现起来比最近临域插值算法要复杂得多,我们需要使用几何中心对称的方法获取原图像src的像素点(SrC_x,srC_y),然后找到将用于计算插值的四周的四个点的坐标(SrC_×0,srC_y0)、(src_×0,srC_y1)、(srC_×1,src_y0)、(src_x1.srC_y1),最后根据双线性插值算法进行缩放。这里需要注意的是,由于我们将最终的dst像素点作为一个整体计算,因此在循环的时候我们需要把颜色通道带上。
双线性插值算法虽然计算量较大,但是缩放后的图像质量高,不会像最近临域插值算法那样可能出现像素值不连续的的情况。但是,由于双线性插值算法具有低通滤波器的性质,使高频分量受损,所以可能会使图像轮廓在一定程度上变得模糊。

标签:算法 c中 使用 算法实现 ima 图像 idt 情况 默认
原文地址:https://www.cnblogs.com/liming19680104/p/12205010.html