标签：后缀   ali   info   编号   字符   lock   方便   技术   奇数   

回文树

本文全文引自yijan，特此鸣谢。

回文树，也就是回文自动机，PAM(Palindrome automaton) 是一个处理回文串的有力工具。然而这个东西比SAM简单多了。。

（它可能比 manacher 要强得多？）

回文自动机有两个根，也就是说其实是有两个树的，一个存储长度为奇数的回文串一个存储长度为偶数的回文串。

回文自动机上的每一个节点表示一个本质不同的回文串。也就是说回文自动机上的节点个数就是本质不同的回文串个数。

• 一些定义
  • $ len[p] $ 表示 $ p $ 节点所代表回文串长度
  • $ fail[p] $ 表示 $ p $ 节点的最长回文后缀所在的节点。
  • $ son[p][c] $ 表示 $ p $ 节点代表回文串两边分别加上字母 $ c $ 得到的回文串的节点。

由于回文树的构造方法类似后缀自动机采用增量法，有一个重要的结论：

• 每次在当前的字符串结尾添加一个字母，如果新增了回文串，那么新增的本质不同回文串必然是添加后的字符串的最长回文后缀这一个。

  证明很简单，画图有：

  

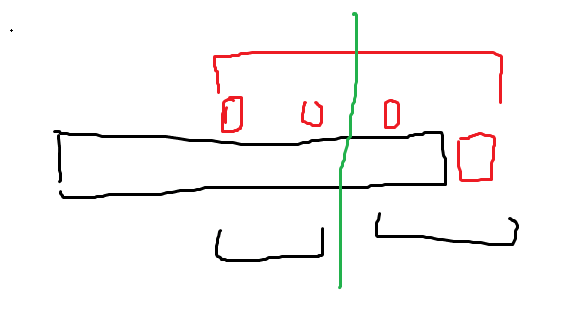
  如果最左边的红色和最右边的红色构成的是最长回文后缀，并且有一个更短的后缀，它一定已经出现过了。

  同时这也证明了本质不同的回文个数是 $ O(n) $ 的。

• 构造回文树

  • 首先，初始状态只有两个点，$ t_0,t_1 $ 分别表示奇数回文串个数和偶数回文串个数。我们有 $ len[t_0] = -1 , len[t_1] = 1 $。因为单个字符也是回文串，相当于是 $ t_0 $ 两边分别加一个字符，长度变为 1 。我们让它们的 fail 指针指向对方（没什么意义，只是方便，这样做了可以方便得把所有回文串联系起来）。

  • 用 last 表示插入上一个字符后，当前最长回文后缀所在节点的编号。开始是 0 或者 1。当我们插入一个字符，从 last 向上（fail指针）跳，直到第一个位置使得这个回文串的左边一个字符和这个位置的字符相同。这样找到的必然是最长回文后缀。
  • 加入我们找到的节点是 $ p $ 插入的字符是 $ c $ ，先检查一下 $ son[p][c] $ 是否存在。如果存在就说明都出现过了，直接结束。否则新建一个节点 $ q $ 并且 $ len[q] = len[p] + 2 $ 。

  • 这个时候要考虑 $ q $ 的 fail 指针。做法就是继续沿着 $ p $ 向上跳，知道找到又一个满足条件的位置。这个就必然是 $ q $ 的最长回文后缀辣。最后更新一下last即可。

  复杂度是 $ O(n) $ 但是我不会证。

贴个板子

struct PAM {
    int next[maxn][ALP] , fail[maxn] , cnt[maxn] , num[maxn] , len[maxn] , s[maxn];
    int last, n, p;
    struct edge {
        int v, nxt;
    } e[maxn];
    int ecnt, head[maxn];
    bool vis[maxn];

    void adde(int u, int v) {
        e[++ecnt].v = v;
        e[ecnt].nxt = head[u];
        head[u] = ecnt;
    }

    int newnode(int l) {
        for (int i = 0; i < ALP; i++)
            next[p][i] = 0;
        cnt[p] = num[p] = 0;
        len[p] = l;
        return p++;
    }

    void init() {
        vis[0] = vis[1] = 0;
        ecnt = 0;
        for (int i = 0; i <= p; ++i) head[i] = 0;
        p = 0;
        newnode(0);
        newnode(-1);
        last = 0;
        n = 0;
        s[n] = -1;
        fail[0] = 1;
    }

    int get_fail(int x) {
        while (s[n - len[x] - 1] != s[n]) x = fail[x];
        return x;
    }

    void add(int c) {
        c = c - 'a';
        s[++n] = c;
        int cur = get_fail(last);
        if (!next[cur][c]) {
            int now = newnode(len[cur] + 2);
            fail[now] = next[get_fail(fail[cur])][c];
            next[cur][c] = now;
            num[now] = num[fail[now]] + 1;
        }
        last = next[cur][c];
        cnt[last]++;
    }

    void count() {
        for (int i = p - 1; i >= 0; i--)
            cnt[fail[i]] += cnt[i];
    }

    void build() {
        for (int i = 0; i <= p - 1; ++i)
            adde(fail[i], i);
    }

}pam;  

[算法模版]回文树

标签：后缀   ali   info   编号   字符   lock   方便   技术   奇数   

原文地址：https://www.cnblogs.com/GavinZheng/p/12210034.html