python计算年利率

标签：而不是   margin   怎样   pytho   mat   round   span   strong   计算   

一、现金分期年利率

现在很多人都有使用网上借贷，动不动就消费分期。经过了解很多对贷款利率有一些误解，粗看觉得产生的利息也不是很高，但是年化利率到第是多少，这里面的玩法是怎样的呢。

拿某个借贷平台举例，比如借款10000元，分12期还完。每月需要还款约912.69。

图片不完全，每个月金额差不多，12期

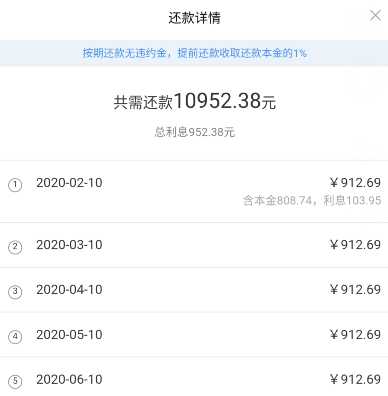
不仔细分析的话，很多借款平台有显示出借款的日利率是多少，而消费分期一般往往只显示了每月还款数或利息数，利率是多少则自己经过一番计算。比如上面的例子按照表面的逻辑陷阱计算利率就是：952.38/10000=9.52%，也就是说年利率是9.52%。这样计算就错了。

实际利率计算是有现成公式的，这个涉及到货币时间价值的一些知识，公式计算如下：

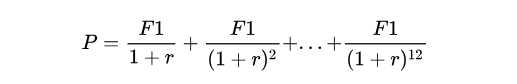
其中，P为本金，F为每期现金流，r为月利率（内部收益率IRR）。有公式就好办了，Python的numpy有现成的IRR计算公式，分分钟搞定

import numpy_financial as npf

# 计算内部收益率
irr = round(npf.irr([-10000, 912.69, 912.69, 912.69, 912.69, 912.69, 912.69, 912.69, 912.69 ,912.69, 912.69, 912.69, 912.79,]), 5)
print("内部收益率IRR = {}%".format(irr*100))

# 计算年化收益率（复利公式）
pa = round((irr+1)**12 - 1,4)
print("实际年化贷款利率 = {}%".format(pa*100))

运行结果为：

内部收益率IRR = 1.428%
实际年化贷款利率 = 18.55%

年化利率为复利（利滚利），因此用这个公式：

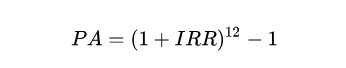
 所以你看到了吧，实际的年化利率是18.55%，而不是9.52%。

二、定投收益率计算

A和B两个人都去买基金，他们都有10000块钱。
A定投，每个月投资833.33块钱，投了12个月，总投资10000，最终金额是10952，最终收益率=（10952-10000）/10000=9.52%；
B一次性购买，第一个月就购买了10000，12个月后最终金额也是10952，最终收益率=（10952-10000）/10000=9.52%；
最终他们的年化收益率是多少呢？
B很明显，就是9.52%，但是A呢？他第11个月投入的833.33才放了一个月而已，你要让这部分的钱收益算成是12个月的，这样算年化收益是有问题的。
那应该怎么算呢？就是IRR公式，打开Excel表格，将每个月投入和最终金额输入，然后使用=IRR(B1:B13)这个公式。

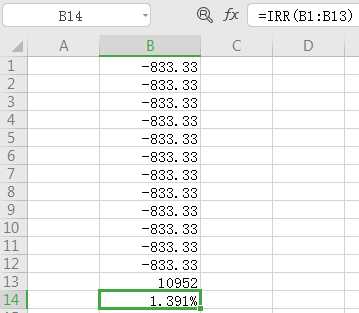
但这里计算出来的是每期收益率，我们应该算一下年化收益=(IRR(B1:B13)+1)^12-1

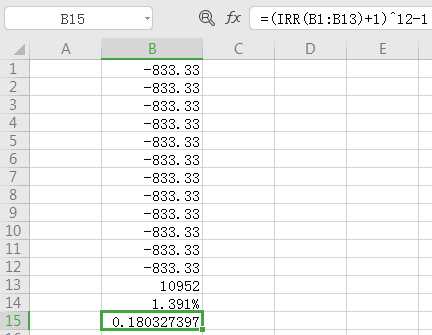
对，没错，这个才是A的真实年化收益率18.03%，接近B的9.52%两倍！！！

当然下次如果有类似每月同样金额然后计算最终收益率，如果你不想这么麻烦，毛估估直接*2也是没太大问题的

python的计算方法如下：

import numpy_financial as npf

profile = npf.irr([833.33, 833.33, 833.33, 833.33, 833.33, 833.33, 833.33, 833.33, 833.33, 833.33, 833.33, 833.33, -10952])
print (profile)
print(pow(profile+1, 12) - 1)

运行结果如下：

0.013911869738689298
0.18032739694153732

python计算年利率

标签：而不是   margin   怎样   pytho   mat   round   span   strong   计算   

原文地址：https://www.cnblogs.com/steven223-z/p/12218748.html