标签:还需要 很多 怎么 维基百科 删除节点 导致 最大值 连续 面试
红黑树相信经过面试官折磨的人都不会太陌生,作为数据结构中较复杂都一种,一直是面试中面试官常用的虐杀手段。废话不多说,直接进入正题。
在了解红黑树之前,先要了解二叉查找数,又叫二叉树。二叉树顾名思义,是一种每个节点最多有两个子节点都树,同时遵循 左节点的值<父节点的值<右节点的值 这样的规律,如下图所示。
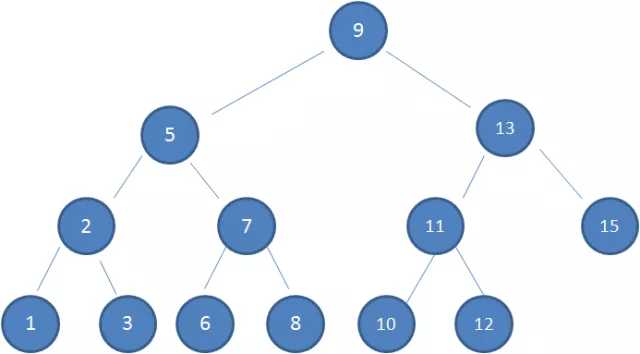
它是一种查找次数小于等于树高的数据结构。如图中树有4层,即树高为4,当我们需要查找8时,经过的路线是这样的:
1、8<9,往左查找
2、8>5,往右查找
3、8>7,往右查找
4、8=8,找到结果
总共查找4次,等于树高。这棵树不管怎么找,查找次数总是小于等于树高。
二叉树的插入同样遵循上述规则,会一步一步对比,从而找到插入的位置,可以想象上图中的8不存在,而是需要插入一个8,结果与上述路线一致。
二叉树的删除会涉及到无子节点和有子节点两种情况,无子节点直接删除即可,有子节点会需要用左边最大值或右边最小值替换当前删除节点,具体不细聊。
当二叉树插入数值不均衡时,会出现树结构的变形与查找性能的损耗,比如现在二叉树有8,9,12三个值,然后需要插入7,6,5,4,3这五个值时,产生的结构如下图所示。
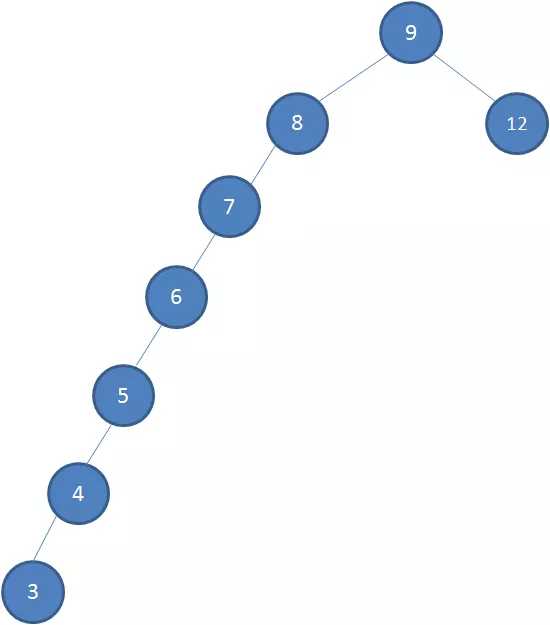
树高会不合理的增高,查找效率也无法得到保证。红黑树就是为了解决这种情况而诞生的。
红黑树又称为自平衡二叉树,它符合二叉树的规则同时比它的规则更加的复杂,具体规则如下:
1、所有节点都是红色或黑色
2、根节点为黑色
3、所有叶子都是黑色(NIL节点)
4、每个红色节点必须有两个黑色的子节点。(不能有两个连续的红色节点。)
5、从任一节点到其每个叶子的所有简单路径(不要回退)都包含相同数目的黑色节点。
具体样子如下图所示:

解释一下几个规则的含义:
1,2很好理解,节点都是红和黑,根节点是黑色的。
3所有叶子都是黑色的,叶子与叶子节点是两个概念,叶子不是一个节点,可以理解为没有数值的空节点,也就是图中的NIL。
4也很好理解,红色节点的子节点都是黑色的,这就保证了没有两个连续的红色节点。
5稍微解释一下,简单路径就是说一次到底,不要回退,叶子就是NIL,比如从8这个节点出发,不管是去1下面的叶子,11下面的叶子,还是6下面的叶子,都是经过一个黑色节点,从任何节点出发都是一样的规则,经过相同数量的黑色节点。
以上5个规则,加上二叉树的规则,就组成了红黑树这一极具特点的树型数据结构。
红黑树的查找与二叉树类似,都是查找次数小于等于树高,但红黑树由于平衡的规则会使树高相对平衡,不会出现某条路径远远大于其他路径的情况。
红黑树的插入较为复杂,有时为了维持规则需要做结构的调整,常用的调整手段是改变颜色、左旋转和右旋转。由于规则5,如果插入的值为黑色节点,会导致黑色节点数量很难相同,所以默认每次插入的值都为红色节点。和二叉树一样,通过对比找到插入的位置,默认插入一个红色节点的数值,这里会分为很多情况,大概列举如下:
1、插入位置为根节点(第一个值),红色变成黑色即可。
2、插入位置父节点为黑色节点,直接插入一个红色节点即可。此时1,2,3规则都不会违背,由于父节点为黑色,4也没有违背。由于插入的是红色节点,5也没有违背,所以红黑树不需要做调整,直接插入即可。
3、插入位置父节点与父节点的同级节点(下称叔父节点)均为红色节点,需要改变父节点和叔父节点的颜色为黑色,同时将父节点的父节点(下称祖父节点)改变为红色。如果祖父节点为根节点或祖父节点的父节点也为红色,需要进一步变化。可以理解为把祖父节点带入这个方法逻辑中,类比为插入祖父节点,从而判断祖父节点需要如何变化。
4、插入位置父节点为红色,叔父节点为黑色或者空节点,同时新增节点是其父节点的右子节点而父节点又是其父节点的左子节点时,需要使用到左旋转,如图所示。N为插入的节点,P为它的父节点。左转换逆时针旋转P节点与它的两个子节点,同时将N节点下的2节点给到P节点。两个红色一起违反规则4,可再将N节点变更为黑色。
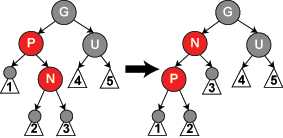
5、插入位置父节点为红色,叔父节点为黑色或者空节点,同时新增节点是其父节点的左子节点而父节点又是其父节点的左子节点时,需要使用到右旋转,如图所示。N为插入的节点,P为它的父节点,G为P的父节点。右转换顺时针旋转N,P,G三个节点,同时将P节点下的3节点给到G节点。再改变P和G的颜色即可。
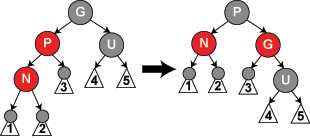
6、插入位置父节点是其父节点的右子节点时,与上述4,5情况完全相反,即只要将4和5中的所有左换成右,所有右换成左,就是这种插入情况的处理方法。
红黑树的删除同样复杂,删除的节点有各种各样的情况,但我们可以统一类化为删除的节点只有一个子节点的情况。如果删除的节点有两个子节点,与二叉树类似,红黑树也是需要找到左子树中的最大值或右子树中的最小值,将数值做替换,等于删除的是左子树中的最大值或右子树中的最小值,这个值一定不会有两个子节点,而只是数值的替换,颜色保持不变,所以不会破坏规则。如果删除的节点没有子节点,可以将一个空节点当成它的子节点。所以我们只需要考虑删除的节点只有一个子节点的情况。
1、删除节点为红色的情况。删除节点为红色,根据规则4,它的儿子一定是黑色,此时只要删除当前节点即可,它的儿子是黑色,所以不会破坏规则3和4,同时路径中只是缺少了一个红色的节点,也不会破坏规则5.
2、删除的节点为黑色,它的儿子是红色的情况。这种情况也很简单,将当前节点删除,将它的儿子从红色改变成黑色即可。
3、删除的节点为黑色,它的儿子也是黑色的情况。这种情况比较复杂,暂时不介绍了,可看维基百科对红黑树的介绍。
红黑树的结构、规则和实现方式大致介绍完了。面试中经常会问的大概就是结构与规则,以及它的平衡方法,改变颜色、左旋转和右旋转。还需要了解它的时间复杂度O(logn)、应用场景与好处。想要更多了解可以参考维基百科对红黑树的介绍,还是非常详细的。
标签:还需要 很多 怎么 维基百科 删除节点 导致 最大值 连续 面试
原文地址:https://www.cnblogs.com/dtt-java/p/12228642.html