标签:例子 学习二 颜色 并且 表示 ima 但我 情况 种类型
我们在生活中用到数字,都是以十进制的方式计数的。稍有计算机常识的人都知道,计算机中是以二进制的方式计数的,另外在计算机中表示颜色经常会用到十六进制的数字,此外在其他一些领域还会用到八进制的数字。那么二进制、八进制、十进制、十六进制的数字,究竟是怎样计数的?它们之间是怎样相互换算的?本文就来详细说说这两个问题。首先来说我们最熟悉的十进制。十进制计数法有10个原始的数字,分别是0-9,当我们想表示一个比9还大1的数字时,1个数位就不够用了,必须用两位数来表示,就是10,再比10大1的数是11...以此类推这样就能表示出任意大的数字。
而计算机中使用的二进制计数法,二进制计数法只有两个原始数字,就是0和1,想表示比1还大1的数字就需要用两位数来表示,就是10,之后是11,再之后是100...二进制计数法中最大的数字就是1,再增加的话就要进位了。这样以此类推也能表示任意一个数字。
通过学习二进制计数法,想必大家已经知道八进制数的特点了,那就是总共有8个原始数字,分别是0-7,当表示比7还大1的数字时,就必须进位了。
那么再来说说十六进制计数法。十六进制计数法中,有16个原始数字,前10个原始数字我们就用0-9来表示,但我们习惯使用的阿拉伯数字只有0-9这10个数字,现在还差6个原始数字,怎么办呢?我们就用字母去代替,这样的话第11个原始数字就A,第12个原始数字就是B,以此类推,第16个原始数字就是F。这个F换算成10进制数其实就是15。当表示比F还要大1的数字,就需要进位了,所以F再向后数就是10,11...小伙伴们可能非常不习惯16进制的技术方法,因为突然跑出来一些字母来表示一个数字,其实用多了自然也就习惯了。
下面我们来说说这些数制之间如何相互转换。刚才提到的4种进制的数字,相互转换的话有12种情况,请看下图: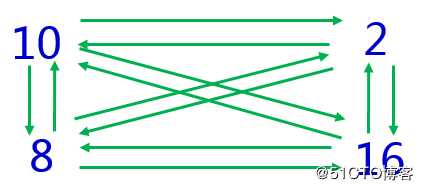
从这幅图片上大家可以看到,各种数制之间相互转换情况的所有情形:四种数制之间相互连线,总共可以连12条线。很多小伙伴的第一反应就是:这么多种情况,又要记很多转换规则。其实大可不必担心,我们可以把这12中情况分成3种类型,并且掌握每种类型的算法就可以了。12种情况可以分成以下三类
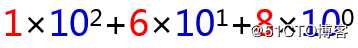
以上算式运算得到的值是168,所以1、6和8这3个原始数字排列起来就能表示168。
这里需要强调一个细节,因为我们现在讨论的是10进制的数字,这三个原始数字都是乘以以10为底的n次方。按照这个原理,如果讨论的是2进制数字,那么计算一个数就应该是原始数字乘以以2为底的n次方,然后再把各个数字相加,最后就能得出这个数字的具体值了,比如一个二进制数101,按照刚才的算法,可以把101分解成以下形式: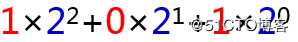
以上算式运算得到的值是5。这就是二进制转换为10进制数的基本原理。
同样的,我们也可以把十六进制和八进制的数转换为十进制,比如十六进制的数1AF,可以分解成如下形式: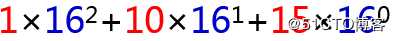
我们在运算时把A和F直接替换成对应的十进制数10和15,以上算式运算最终得到的十进制数就是431。通过几个例子,相信大家已经掌握了其他进制的数转换为十进制数的算法。这个算法的套路就是把各个位上的数字与M为底的n-1次方相乘,然后把相乘的结果都加起来,需要注意的是:几进制转换十进制,那么M就是几,比如要把二进制转换为十进制,这个M就是2。而所谓的n就是从右边数第几位,比如对于从右边数第3位的数字,n就是3,而n-1就是2。
刚才我们讲的是第一种类型,就是把其他进制的数字转换为十进制,下面我们再来说说十进制的数如何转换为其他进制的数。十进制的数如何转换为其他进制的数算法我们可以称之为“辗转求余法”。所谓“辗转求余法”就是指不断的用十进制的数字除以N,直到商为零为止,之后把每次除法操作所得到的余数串起来就完成了转换。这里要说明的是,如果是希望转换为二进制的数,那么就是不断除以2,同理,如果是希望转换为八进制的数,就不断的除以8。我们就以十进制转换为二进制为例来为大家讲解这个算法。比如我们要把十进制的数字13转换为2进制,就可以用以下方式完成转换:

运算的过程如上图所示:把13除以2,得到的商如果不为0,那么就以除法得到的商继续除以2,一直到商为0为止,最后把每次除法操作所得到的余数从下到上串起来,得到的结果就是1101。
下面再来讲一个十进制数转换为十六进制数的例子。比如把1835这个数字转换为十六进制,算法是一样的,只不过这次是不断的用这个数字除以16,过程如下图所示:
把余数中大于9的余数替换为字母,也就是把11替换为B,这样就得到了1835转换为十六进制的数字为72B
以上我们已经讲解了数制之间转换的两种类型,分别是其他进制转换为十进制和十进制转换为其他进制。现在就只剩第三种,那就是其他进制数字之间的转换。首先我们讲一下二进制转换为十六进制数的算法。在讲算法之前,必须先讲一下二进制数和十六进制数有什么关系。我们知道,二进制数只有两个原始数字分别是0和1,也就是说,二进制数的每一个位只有两种情形,非0即1。按照排列组合的算法,如果我们想排列出4种情形,只用1位二进制数是无法实现的,因为二进制数的每一个位只有2种情形。要排列出4种情形,那必须用2位数,同理,想排列出8种情形,要用3位数,想排列出16种情形,必须用4位数。而十六进制数有16个原始数字,也就是说十六进制数仅仅1个位上的数字就都有16种变化的可能性。那么这样我们就很容易理解一个道理,那就是:十六进制数的1位所能表示的数字,相当于二进制数4位所能表示的数字。
按照这种思想,我们把二进制数转换为十六进制的数时,首先把每4位二进制数划分为一组,把每一组二进制数字分别转换为一位十六进制数。划分时候从最右边开始,每4位分为1组,如果划到左边发现不够4位时,就让剩余的这几个数单独划分为一组。例如,二进制数101 1011 1000 1110转换为十六进制数过程如下: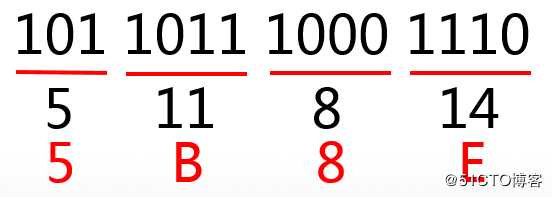
如上图所示:从右边开始,每4位分为一组,左边不足4位的单独划分为一组,之后把每组二进制数先转为十进制数,然后把大于9的数字用字母代替,最后就产生了转换的结果5B8E。
这个例子是把二进制数字转换为十六进制,在转换的时候是把4位二进制数划分为一组进行转换,如果想把一个二进制数字转换为八进制数该怎么办呢?很多同学肯定会立刻想到,在转换的时候把3位二进制数划分为一组,为什么是3位划分一组呢?原因很简单,就是因为每3位二进制数可以排列出8种情形,而八进制数每1位数字就有8种变化的可能性。
我们仍然用刚才这个二进制数字进行举例,其转换过程如下:
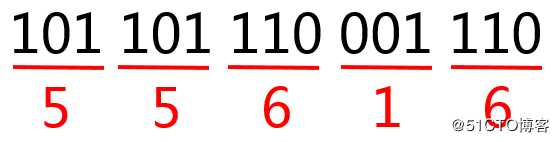
如想系统学习Java编程,欢迎观看我在本站的视频课程。
标签:例子 学习二 颜色 并且 表示 ima 但我 情况 种类型
原文地址:https://blog.51cto.com/2266836/2468308