标签:假设 stream 转移 出现 using 程序实现 for return http
RMQ是询问某个区间内的最大值或最小值的问题,ST算法可以求解RMQ问题.ST算法通常用在要 多次询问某一些区间的问题中,相比于线段树,它的程序实现更加简单,运行速度更快,它可以做到O(nlogn)的预处理,O(1)回答每个问题.使用ST算法的条件是没有修改操作,因此它适用于没有修改操作并且访问次数较多(10^6级别甚至更大)的情况.
1.预处理
ST算法的原理实际上是动态规划,首先要知道f数组的含义,f[i][j]中i表示左边端点,j表示2^j个长度, 因此f[i,j]表示的是区间为[i,i+2^j-1]这个范围内的最大值,也就是以a[i]为起点连续的2^j个数的最大值.由于元素个数为2^j个,所以从中间平均分成两部分,每一部分的个数都为2^(j-1);假设f[6][3]分为f[6][2]和f[10][2],如下图所示,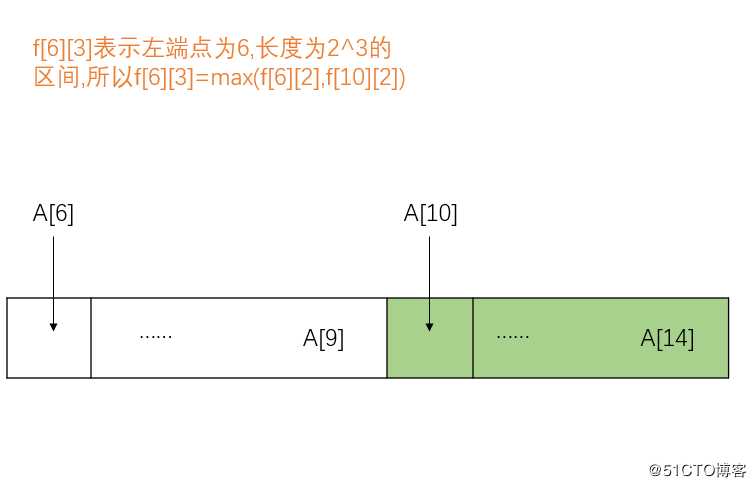
整个区间的最大值一定是左右两部分最大值的较大者,满足动态规划的最优化原理,分析得f数组的状态转移方程为f[i][j]=max(f[i][j-1],f[i+2^(j-1)][j-1]).
for(int j = 1;(1<<j) <= n;++j) //j枚举每一个可能出现的长度
for(int i = 1;i + (1<<j)-1 <= n;i++) //i枚举每一个区间的左端点
f[i][j] = max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
2.询问
当要访问区间[L,R]的最大值,需要知道区间的长度len,mn数组存放的是小于等于一定长度len的最大的2的幂次,若要访问区间[5,10]的最大值,则要先计算出men[len]的值,那么区间[5,10]=[5,8]U[7,10].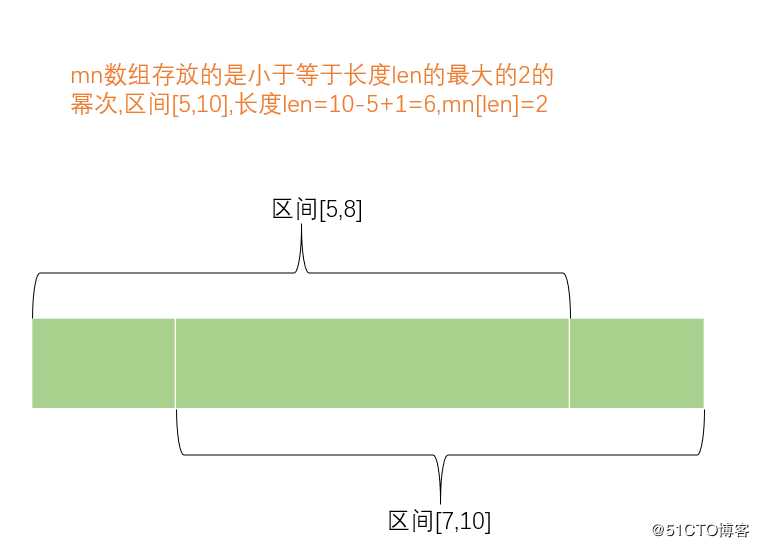
代码实现
//对于一定长度的区间len,mn[len]表示小于等于len的最大的2的幂次
for(int len = 1;len <= n;++len)
{
int k = 0;
while(1<<(k+1) <= len)
k++;
mn[len] = k;
}
3.求区间[x,y]最大值
int k = mn[R - L + 1];
ans = max(f[L][k],f[R-(1<<k)+1][k]);代码实现
#include<iostream>
using namespace std;
const int maxn=1e6+5;
int f[maxn][25];
int mn[maxn];
int a[maxn];
int m,n;
void rmq_init()
{
//初始化所有长度为1的区间的最大值
for(int i = 1;i <= n;i++)
f[i][0] = a[i];
for(int j = 1;(1<<j) <= n;++j) //j枚举每一个可能出现的长度
for(int i = 1;i + (1<<j)-1 <= n;i++) //i枚举每一个区间的左端点
f[i][j] = max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
//对于一定长度的区间len,mn[len]表示小于等于len的最大的2的幂次
for(int len = 1;len <= n;++len)
{
int k = 0;
while(1<<(k+1) <= len)
k++;
mn[len] = k;
}
}
int rmq(int L,int R)
{
int s = mn[R-L+1];
int ans = max(f[L][s],f[R - (1<<s) + 1][s]);
return ans;
}
int main()
{
cin>>n;
for(int i = 1;i <= n;i++)
cin>>a[i];
rmq_init();
int L,R;
cin>>m;
for(int i = 1;i <= m;i++)
{
cin>>L>>R;
cout<<rmq(L,R)<<endl;
}
return 0;
}结果截图
标签:假设 stream 转移 出现 using 程序实现 for return http
原文地址:https://blog.51cto.com/14472348/2468297