遗传算法详解

标签：基因突变   范围   多目标   sel   初始   现在   oss   参数   工作   

遗传算法

1.简要概述

在几十亿年的演化过程中，自然界中的生物体已经 形成了一种优化自身结构的内在机制，它们能够不 断地从环境中学习，以适应不断变化的环境。对于大多数生物体，这个过程是通过自然选择和有性生殖来完成的。自然选择决定了群体中哪些个体 能够存活并繁殖，有性生殖保证了后代基因的混合 与重组。

演化计算（Evolutionary Computation, EC）是在达尔文（Darwin）的进化论和孟德 尔（Mendel）的遗传变异理论的基础上产生的一种在基因和种群层次上模拟自然界生 物进化过程与机制，进行问题求解的自组织、自适应的随机搜索技术。它以达尔文进化论的“物竟天择、适者生存”作为算法的进化规则，并结合孟德尔的遗 传变异理论，将生物进化过程中的繁殖（Reproduction）、变异（Mutation）、竞争 （Competition）、选择（Selection）引入到了算法中，是一种对人类智能的演化模拟方法演化计算的主要有遗传算法、演化策略、演化规划和遗传规划四大分支。其中，遗传算 法是演化计算中最初形成的一种具有普遍影响的模拟演化优化算法。

遗传算法简称GA（Genetic Algorithms）是1962年由美国Michigan大学的Holland教授提出的模拟自然界遗传机制和生物进化论而成的一种并行随机搜索最优化方法。
遗传算法是以达尔文的自然选择学说为基础发展起来的。

自然选择学说包括以下三个方面：
遗传：这是生物的普遍特征，亲代把生物信息交给子代，子代总是和亲代具有相同或相似的性状。生物有了这个特征，物种才能稳定存在。
变异：亲代和子代之间以及子代的不同个体之间的差异，称为变异。变异是随机发生的，变异的选择和积累是生命多样性的根源。
生存斗争和适者生存：具有适应性变异的个体被保留下来，不具有适应性变异的个体被淘汰，通过一代代的生存环境的选择作用，性状逐渐与祖先有所不同，演变为新的物种。

2.基本原理

遗传算法将“优胜劣汰，适者生存”的生物进化原理引入优化参数形成的编码串联群体中，按所选择的适应度函数并通过遗传中的复制、交叉及变异对个体进行筛选，使适应度高的个体被保留下来，组成新的群体
新的群体既继承了上一代的信息，又优于上一代这样周而复始，群体中个体适应度不断提高，直到满足一定的条件遗传算法的算法简单，可并行处理，并能得到全局最优解。

3.基本操作

遗传算法的基本操作有三种：

1. • 复制（Reproduction Operator）
   • 从一个旧种群中选择生命力强的个体产生新种群的过程
   • 具有高适应度的个体更有可能在下一代中产生一个或多个子孙
   • 模拟无性繁殖
2. • 交叉（Crossover Operator）
   • 复制操作能从旧种群中选择出优秀者，但不能创造新的染色体
   • 交叉模拟了生物进化过程中的有性繁殖现象，通过染色体的交换组合，产生新的优良品种
   • 交叉的过程：在匹配池中任选两个染色体，随机选择一点或多点交换点位置；交换双亲染色体交换点右边的部分，即可得到两个新的染色体数字串
3. • 变异(Mutation Operator)
   • 模拟生物在自然的遗传环境中由于各种偶然因素引起的基因突变
   • 以很小的概率随机地改变遗传基因（表示染色体的符号串的某一位）的值
   • 在染色体以二进制编码的系统中，它随机地将染色体的某一个基因由1变为0，或由0变为1

变异的重要作用：没有变异，则无法在初始基因组合以外的空间进行搜索；使进化过程在早期就陷入局部解而进入终止过程；为了在尽可能大的空间中获得质量较高的优化解（水至清则无鱼）

4.应用领域

1. 函数优化：非线性、多模型、多目标的函数优化问题，采用其他优化方法较难求解，而遗传算法却可以得到较好的结果
2. 组合优化：随着问题的增大，组合优化问题的搜索空间也急剧扩大，采用传统的优化方法很难得到最优解
3. 自动控制：利用遗传算法进行控制器参数的优化；基于遗传算法的模糊控制规则的学习；基于遗传算法的参数辨识；基于遗传算法的神经网络结构的优化和权值学习
4. 机器人：移动机器人路径规划、关节机器人运动轨迹规划、机器人结构优化和行为协调
5. 图像处理：图像处理过程中的扫描、特征提取、图像分割等的优化计算；模式识别、图像恢复、图像边缘特征提取

5.关键概念

（1）编码

研究生物遗传是从染色体入手的

染色体是由基因排成的串，可以理解为生物编码

研究遗传算法，研究如何编码是第一步工作

编码是通过某种机制把求解问题抽象为由特定符号按一定顺序 排成的串

使用二进制串进行编码是常见的方法

利用遗传算法求下列一元函数的最大值，其中x∈[-1,1]，求解结果精确到6位小数，请问如何编码？

f(x)=x*sin(8πx)+3.0

【解】由于区间长度为2，求解结果精确到6位小数，因此可以将自变量定义区间划分为等份。又因为2^20 < 2*10^6 < 2^21，所以本例的二进 制编码长度至少需要21位，本例的编码过程实质上是将区间[-1,1]内对 应的实数值转化为一个二进制串（ ）

（2）初始种群

确定编码方案后，遗传算法通常采用随机方法生成若干个个体的集合，该集合称为初始种群，初始种群中个体的数量称为种群规模。

（3）适应度函数

遗传算法对一个个体（解）的好坏用适应度函数值来评价

适应度函数值越大，解的质量越好

适应度函数是遗传算法进化过程的驱动力，也是进行自然选择的唯一标准，它的设计应结合求解问题本身的要求而定

遗传算法使用选择运算来实现对群体中的个体进行优胜劣汰操作：适应度高的个体被遗传到下一代群体中的概率大；适应度低的个体，被遗传到下一代群体中的概率小

（4）遗传算子

• 选择操作的任务就是按某种方法从父代群体中选取一些个体，遗传到下一代群体
• 选择算子采用轮盘赌选择方法，又称比例选择算子，它的基本思想是： 各个个体被选中的概率与其适应度函数值大小成正比。设群体大小为n ，个体i 的适应度为 Fi ，则个体i 被选中遗传到下一代群体的概率为：
• 轮盘赌选择方法的实现步骤如下：
  ①计算群体中所有个体的适应度函数值（需要解码）
  ②利用比例选择算子的公式，计算每个个体被选中遗传到下一代群体的概率
  ③采用模拟赌盘操作（即生成0到1之间的随机数与每个个体遗传到下一代群体的概率进行匹配）来确定各个个体是否遗传到下一代群体中

（5）交叉运算

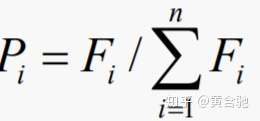
交叉运算是指对两个相互配对的染色体依据交叉概率 Pc 按某种方式相互交换其部分基因，从而形成两个新的个体。交叉运算是遗传算法区别于其他进化算法的重要特征，它在遗传算法中起关键作用，是产生新个体的主要方法。交叉算子一般采用单点交叉算子：

交叉前(用”|"来表示交叉点)：

00000|01110000000010000

11100|00000111111000101

交叉后：

00000|00000111111000101

11100|01110000000010000

（6）变异运算

所谓变异运算，是指依据变异概率 Pm 将个体编码串中的某些基因值用其它基因值来替换，从而形成一个新的个体。

遗传算法中的变异运算是产生新个体的辅助方法，它决定了遗传算法的局部搜索能力，同时保持种群的多样性，交叉运算和变异运算的相互配合，共同完成对搜索空间的全局搜索和局部搜索，变异算子采用基本位变异算子。基本位变异算子是指对个体编码串随机指定的某一位或某几位基 因作变异运算。对于基本遗传算法中用二进制编码符号串所表示的个体，若需要进行变异操作的原有基因值为0，则变异操作将其变为1；反之，若原有基因值为1，则变异操作将其变为0

变异前： 000001110000000010000

变异后： 000001110001000010000

6.遗传算法应用实例

①函数最值问题

利用遗传算法求函数最值（极值）问题是清晰地理解遗传算法的一个较好的途径

【例】求函数f(x1,x2)=x1^2+x2^2的最大值，其中x1 及x2取值范围为{1,2,3,4,5,6,7}

②编码

本例用无符号二进制整数来表示，因 x1, x2 为 0 ~ 7之间的整数，分别用3位无符号二进制整数来表示

将它们连接在一起所组成的6位无符号二进制数就形成了个体的基因型，表示一个可行解

如：基因型X＝101110所对应的表现型是：x＝[ 5，6 ]。个体的表现型x和基因型X之间可通过编码和解码程序相互转换

③初始群体的产生

遗传算法是对群体进行的进化操作，需要给其准备一些表示起始搜索点的初始群体数据

本例中，群体规模的大小取为4，即群体由4个个体组成，每个个体可通过随机方法产生

如：011101，101011，011100，111001

④适应度计算

遗传算法以个体适应度的大小来评定各个个体的优劣程度，从 而决定其遗传机会的大小

本例中，目标函数总取非负值，并且是以求函数最大值为优化目标，故可直接利用目标函数值作为个体的适应度

⑤选择运算

选择运算(或称为复制运算)把当前群体中适应度较高的个体按某种规则或模型遗传到下一代群体中，一般要求适应度较高的个体将有更多的机会遗传到下一代群体中

采用与适应度成正比的概率来确定各个个体复制到下一代群体中的数量。其具体操作过程是：

• 先计算出群体中所有个体的适应度的总和
• Σfi ( i=1.2,…,M );
• 其次计算出每个个体的相对适应度的大小 fi / Σfi，它即为每个个体被遗传到下一代群体中的概率
• 每个概率值组成一个区域，全部概率值之和为1
• 最后再产生一个0到1之间的随机数，依据该随机数出现在上述哪一个概率区域内来确定各个个体被选中的次数

⑥交叉运算

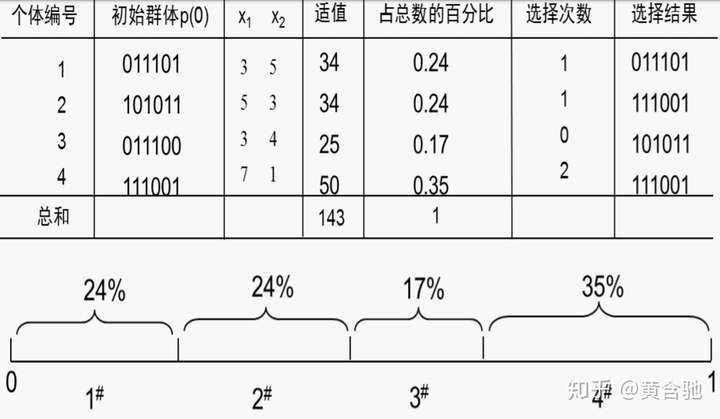
交叉运算是遗传算法中产生新个体的主要操作过程，它以某一概率相互交换某两个个体之间的部分染色体。本例采用单点交叉的方法，其具体操作过程是：先对群体进行随机配对，其次随机设置交叉点位置；最后再相互交换配对染色体之间的部分基因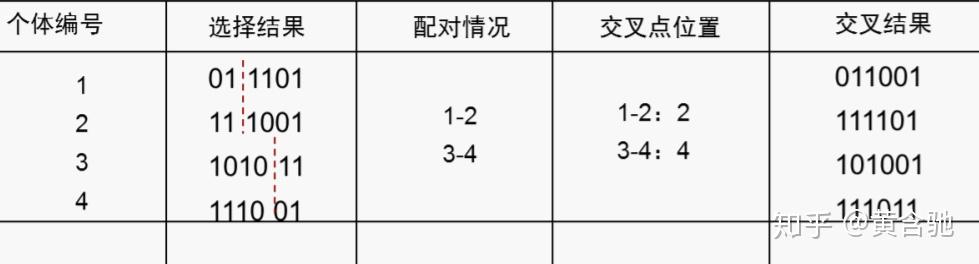

其中新产生的个体“111101”、“111011”的适应度较原来两个个体的适应度都要高

⑦变异运算

变异运算是对个体的某一个或某一些基因座上的基因值按某一较小的概率进行改变，它也是产生新个体的一种操作方法。本例中，我们采用基本位变异的方法来进行变异运算，其具体操作过程是：首先确定出各个个体的基因变异位置，下表所示为随机产生的变异点位置，其中的数字表示变异点设置在该基因座处；然后依照某一概率将变异点的原有基因值取反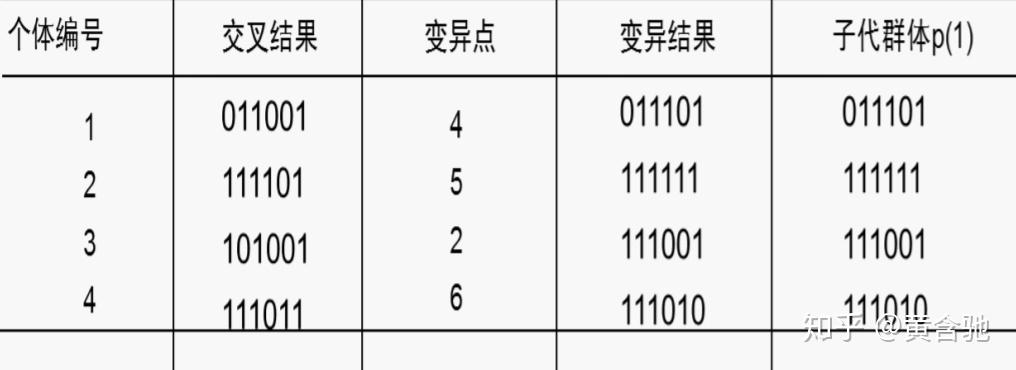

⑧新一代

对群体P(t)进行一轮选择、交叉、变异运算之后可得到新一代的群体p(t+1)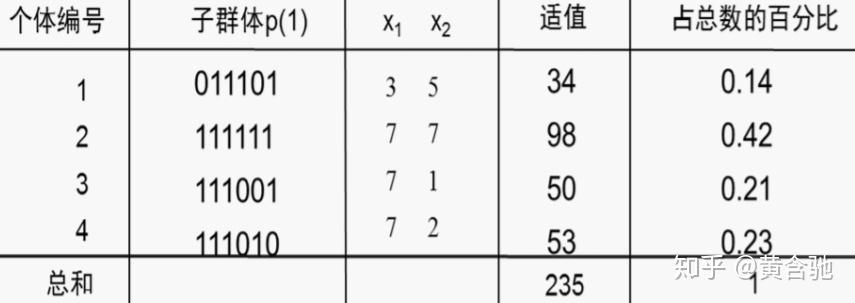

群体经过一代进化之后，其适应度的最大值、平均值都得到了明显的改进。事实上，这里已经找到了最佳个体“111111”

https://zhuanlan.zhihu.com/p/93749379

遗传算法详解

标签：基因突变   范围   多目标   sel   初始   现在   oss   参数   工作   

原文地址：https://www.cnblogs.com/wangxiaozhang/p/12241354.html