标签:plot mat gradient 比较 gre image png reg bat
1、梯度下降思想在数学中的梯度下降是:
xk+1 = xk + λkPk
λk表示步长
Pk表示方向,沿梯度方向下降最快
沿着方向不断更新x,直到x达到最小
为了得到最好的拟合线,我们的目标是让损失函数达到最小
因此,引入梯度下降的思想:
条件:有一个J(θ0,θ1)
目标:让J(θ0,θ1)最小
步骤:
1、初始化θ0,θ1
2、持续改变θ0,θ1的值,让J(θ0,θ1)越来越小
3、直到得到一个J(θ0,θ1)的最小值
2、梯度下降算法
重复执行: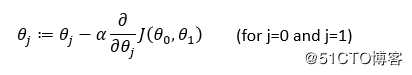
其中:α为学习率,也是步长
求偏导部分(也就是求梯度)是下降方向
线性回归用到的是同步更新
不论斜率正或负,梯度下降都会逐渐趋向最小值
如果α太小的话,梯度下降会很慢
如果α太大的话,梯度下降会越过最小值,不仅不会收敛,还有可能发散
即使α是固定不变的,梯度下降也会逐渐到一个最低点,因为随着梯度下降迭代次数的递增,斜率会趋于平缓,也就是说,倒数部分会慢慢变小
至于怎么选取α,下面会讲到
3、线性回归的梯度下降
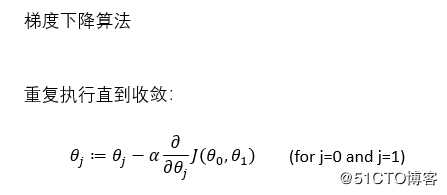

四、三种梯度下降
1、批梯度下降
批梯度下降Bath Gradient Descent:
指每下降一步,使用所有的训练集来计算梯度值
import numpy as np
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
X_b = np.c_[np.ones((100, 1)), X]
#print(X_b)
#学习率α
learning_rate = 0.1
#通常在做机器学习的时候,一般不会等到它收敛,太浪费时间,所以会设置一个收敛次数n_iterations
n_iterations = 1000
#样本数
m = 100
#1.初始化 θ0 , θ1
theta = np.random.randn(2, 1)
count = 0
#4. 不会设置阈值,之间设置超参数,迭代次数,迭代次数到了,我们就认为收敛了
for iteration in range(n_iterations):
count += 1
#2. 接着求梯度gradient
gradients = 1.0/m * X_b.T.dot(X_b.dot(theta)-y)
#3. 应用公式不断更新theta值
theta = theta - learning_rate * gradients
print(count)
print(theta)运行结果: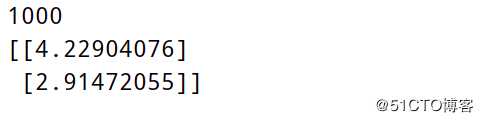
这里其实我还是想拿矩阵来解释一下
函数 hθ(x) = -4000 + 12000x
当x = 120 , 150 时,方程可由矩阵表示为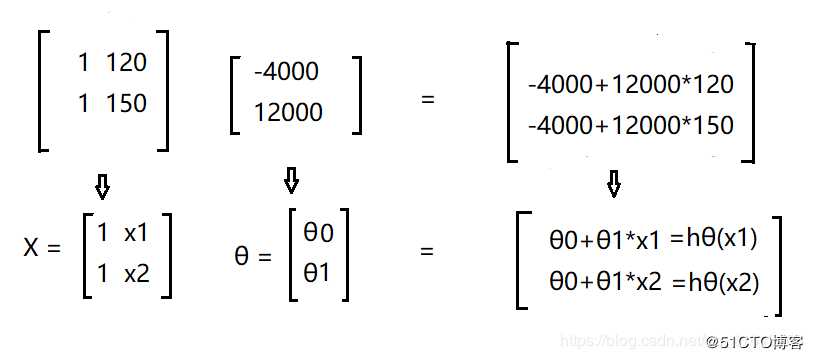
代码中:
np.c_[ ] 表示把2个维度相同的矩阵拼在一起
np.ones((100,1)) 表示100行1列元素全是1的矩阵
np.dot(a,b) 表示矩阵a和b点乘,或者写为 a.dot(b)
.T 表示求矩阵的转置
计算梯度的这段代码: gradients = 1.0/m * X_b.T.dot(X_b.dot(theta)-y)
为了方便起见,就以2个样本数量x1,x2 来解释吧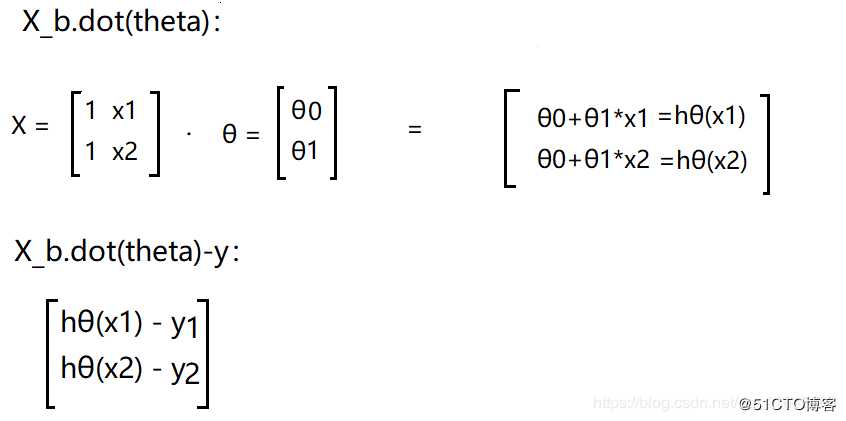
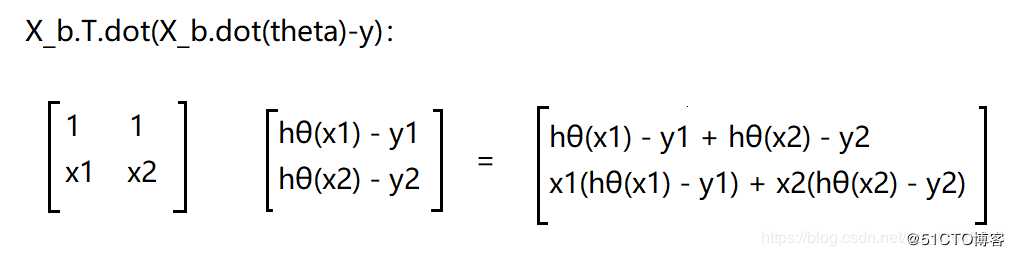
再除以m : 1.0/m X_b.T.dot(X_b.dot(theta)-y) ,就相当于红框中的这一部分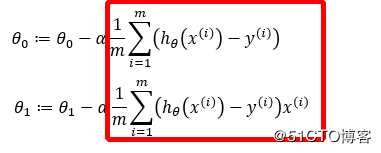
因此:不断更新的theta值就为:
theta = theta - learning_rate gradients
2、随机梯度下降
随机梯度下降Stochastic Gradient Descent
指的是每下降一步,使用一条训练集来计算梯度值
把m个样本分成m份,每次用1份做梯度下降;也就是说,当有m个样本时,批梯度下降只能做一次梯度下降,但是随机梯度下降可以做m次
有一个概念:epoch 轮次
1 epoch = 1次遍历所有的数据
对于批梯度下降来说,1次梯度下降就是1epoch
对于随机梯度下降来说,需要做m次才是1epoch
import numpy as np
import random
x = 2 * np.random.rand(100, 1)
y = 4 + 3 * x + np.random.randn(100 ,1)
X = np.c_[np.ones((100, 1)), x]
n_epochs = 500 # 轮次
learning_rate = 0.1 # 学习率
m = 100 # 样本数
num = [i for i in range(m)] # 列表num:0 ~ 99
theta = np.random.rand(2, 1) # 初始化theta值
#做500epoch,一次处理1条,一个epoch循环100次
for epoch in range(n_epochs):
rand = random.sample(num, m) # 在列表num中随机选取100个数字,其实是将顺序打乱
#print(rand)
for i in range(m):
random_index = rand[i] # rand是一个列表,拿到列表中的每一个元素作为索引
xi = X[random_index: random_index+1] # 随机选取一个样本
yi = y[random_index: random_index+1]
gradients = xi.T.dot(xi.dot(theta) - yi) #只选取了1个样本,所以乘以的是 1/1
theta = theta - learning_rate * gradients
print(theta)运行结果: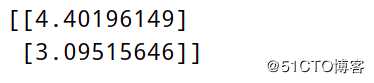
3、Mini-Batch梯度下降
Mini-Batch Gradient Descent
指的是每下降一步,使用一部分的训练集来计算梯度值
如果mini-batch 大小 = m:它就是批梯度下降
如果mini-batch 大小 = 1 :它就是随机梯度下降
如果 1 < mini-batch大小 < m :它就是Mini-Batch梯度下降
import numpy as np
import random
x = 2 * np.random.rand(100, 1)
y = 4 + 3 * x + np.random.randn(100 ,1)
X = np.c_[np.ones((100, 1)), x]
n_epochs = 500 # 轮次
learning_rate = 0.1 # 学习率
m = 100 # 样本数
theta = np.random.rand(2, 1) # 初始化theta值
batch_num = 5 # 循环5次
batch_size = m // 5 # 一次处理20条
#做500epoch, 一次处理20条,一个epoch循环5次
for epoch in range(n_epochs):
for i in range(batch_num): # 循环5次
start = i * batch_size
end = (i + 1) * batch_size
xi = X[start: end]
yi = y[start: end]
gradients = 1 / batch_size * xi.T.dot(xi.dot(theta) - yi) #选取了batch_size个样本,所以乘以 1/batch_size
theta = theta - learning_rate * gradients
print(theta)运行结果:
4、三种梯度下降比较
梯度下降类别 速度 准确度
批梯度下降 最慢 最准确
Mini-Batch梯度下降 中等 中等
随机梯度下降 最快 不准确
如何选择:
随机梯度下降会丧失向量带来的加速,所以我们不太会用随机梯度下降
当训练集比较小时,使用批梯度下降(小于2000个)
当训练集比较大时,使用Mini-Batch梯度下降
一般的Mini-Batch size为:64,128,256,512,1024
Mini-Batch size要适用CPU/GPU的内存
5、学习率衰减
我们在以上代码中还提到了一个概念 α 学习率
一般我们选择α时,可以尝试 :1,0.1,0.2,0.3…
在做Mini-Batch的时候,因为噪声的原因,可能训练,结果不是收敛的,而是在最低点附近摆动,因为α是固定不变的,如果我们要解决这个问题,就需要减少学习率,让步伐不断减小,让他在尽量小的范围内晃动
因此我们在设置了α初始值后,还可以设置它的衰减率,通过不断更新学习率,从而达到要求
实现方法: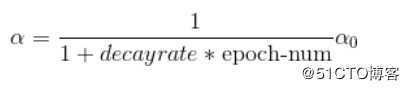
学习率初始值: a0
衰减率:decay_rate
代数:epoch_num,第几次循环
import numpy as np
import random
x = 2 * np.random.rand(100, 1)
y = 4 + 3 * x + np.random.randn(100 ,1)
X = np.c_[np.ones((100, 1)), x]
a0 = 0.1 # 学习率初始值
decay_rate = 1 # 衰减率
#更新学习率
def learning_schedule(epoch_num):
return (1.0 / (1 + decay_rate * epoch_num )) * a0
n_epochs = 500 # 轮次
m = 100 # 样本数
theta = np.random.rand(2, 1) # 初始化theta值
batch_num = 5 # 循环5次
batch_size = m // 5 # 一次处理20条
#做500epoch, 一次处理20条,一个epoch循环5次
for epoch in range(n_epochs):
for i in range(batch_num): # 循环5次
start = i * batch_size
end = (i + 1) * batch_size
xi = X[start: end]
yi = y[start: end]
gradients = (1 / batch_size) * xi.T.dot(xi.dot(theta) - yi)
learning_rate = learning_schedule(i) # 更新的学习率
theta = theta - learning_rate * gradients
print(theta)实现学习率衰减还有其他几种方法: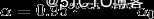


五、多变量线性回归
1、多变量线性回归模型
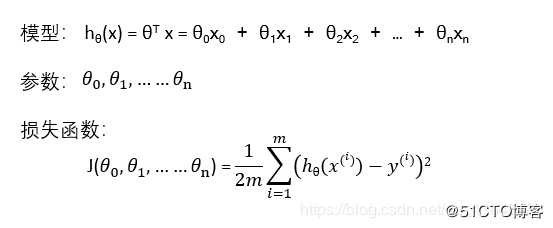
#encoding:utf-8
"""
多项式回归
"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 0.5 * X ** 2 + X + 2 + np.random.randn(m, 1)
plt.plot(X, y, ‘b.‘)
# plt.show()
d = {1: ‘g-‘, 2: ‘r+‘, 10: ‘y*‘}
for i in d:
#include_bias 可以理解为w0 =False 意思就是不要w0
poly_features = PolynomialFeatures(degree=i, include_bias=False)
"""
fit 和 fit_transform的区别
fit: 简单来说,就是求得训练集X的均值,方差,最大值,最小值这些训练集X固有的属性
fit_transform: 首先fit,然后在此基础上,进行标准化,降维,归一化等操作
"""
X_poly = poly_features.fit_transform(X)
#print(X[0])
#print(X_poly[0])
#print(X_poly[:, 0])
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
print(lin_reg.intercept_, lin_reg.coef_)
y_predict = lin_reg.predict(X_poly)
plt.plot(X_poly[:, 0], y_predict, d[i])
plt.show()2、多元梯度下降

import numpy as np
import random
from sklearn.linear_model import LinearRegression
x1=np.array([1,1,1])
x2=np.array([1,1,2])
x3=np.array([2,2,2])
x4=np.array([1,2,3])
x5=np.array([2,3,4])
x=np.c_[x1,x2,x3,x4,x5]
y=np.array([3,4,6,6,9])
lin_reg=LinearRegression()
lin_reg.fit(x.T,y)
print(lin_reg.intercept_,lin_reg.coef_)
x_new=np.array([[12,15,17]])
print(lin_reg.predict(x_new))标签:plot mat gradient 比较 gre image png reg bat
原文地址:https://blog.51cto.com/13810716/2468658