标签:info png 就会 归并排序 inf 规模 lang 数列 --
快速排序
算法步骤:
在数列之中,选择一个元素作为”基准”(pivot),或者叫比较值。
数列中所有元素都和这个基准值进行比较,如果比基准值小就移到基准值的左边,如果比基准值大就移到基准值的右边
以基准值左右两边的子列作为新数列,不断重复第一步和第二步,直到所有子集只剩下一个元素为止。
算法分析:
稳定性:快排是一种不稳定排序,比如基准值的前后都存在与基准值相同的元素,那么相同值就会被放在一边,这样就打乱了之前的相对顺序
比较性:因为排序时元素之间需要比较,所以是比较排序
时间复杂度:快排的时间复杂度为O(nlogn)
空间复杂度:排序时需要另外申请空间,并且随着数列规模增大而增大,其复杂度为:O(nlogn)
归并排序与快排 :归并排序与快排两种排序思想都是分而治之,但是它们分解和合并的策略不一样:归并是从中间直接将数列分成两个,而快排是比较后将小的放左边大的放右边,所以在合并的时候归并排序还是需要将两个数列重新再次排序,而快排则是直接合并不再需要排序,所以快排比归并排序更高效一些,可以从示意图中比较二者之间的区别。
快速排序有一个缺点就是对于小规模的数据集性能不是很好。
示例
假设用户输入了如下数组:

创建变量i=0(指向第一个数据), j=5(指向最后一个数据), k=6(赋值为第一个数据的值)。
我们要把所有比k小的数移动到k的左面,所以我们可以开始寻找比6小的数,从j开始,从右往左找,不断递减变量j的值,我们找到第一个下标3的数据比6小,于是把数据3移到下标0的位置,把下标0的数据6移到下标3,完成第一次比较:
下标

i=0 j=3 k=6
接着,开始第二次比较,这次要变成找比k大的了,而且要从前往后找了。递加变量i,发现下标2的数据是第一个比k大的,于是用下标2的数据7和j指向的下标3的数据的6做交换,数据状态变成下表:
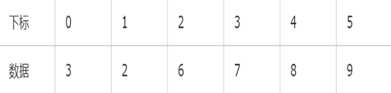
i=2 j=3 k=6
称上面两次比较为一个循环。
接着,再递减变量j,不断重复进行上面的循环比较。
在本例中,我们进行一次循环,就发现i和j“碰头”了:他们都指向了下标2。于是,第一遍比较结束。得到结果如下,凡是k(=6)左边的数都比它小,凡是k右边的数都比它大:
下标
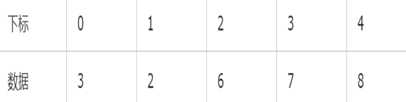
如果i和j没有碰头的话,就递加i找大的,还没有,就再递减j找小的,如此反复,不断循环。注意判断和寻找是同时进行的。
然后,对k两边的数据,再分组分别进行上述的过程,直到不能再分组为止。
注意:第一遍快速排序不会直接得到最终结果,只会把比k大和比k小的数分到k的两边。为了得到最后结果,需要再次对下标2两边的数组分别执行此步骤,然后再分解数组,直到数组不能再分解为止(只有一个数据),才能得到正确结果。
程序示例:
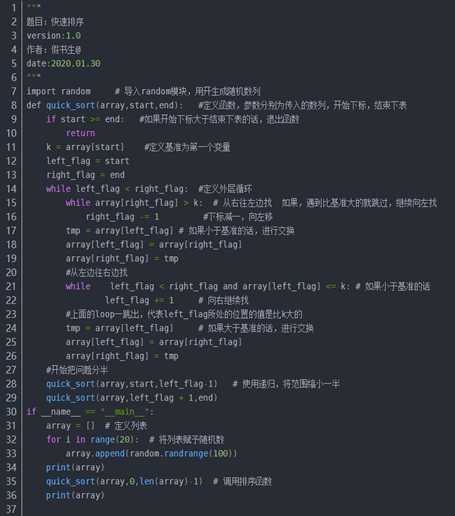
运行结果:
标签:info png 就会 归并排序 inf 规模 lang 数列 --
原文地址:https://www.cnblogs.com/huzhanghui/p/12255582.html