标签:bsp pac color return i++ using 关键字 main 最大
KMP算法是一种非常高效和常用的算法。其核心就是通过预处理一个寻找公共最大前后缀的 Next[ ] 数组,减少匹配失败时的重复无效匹配。
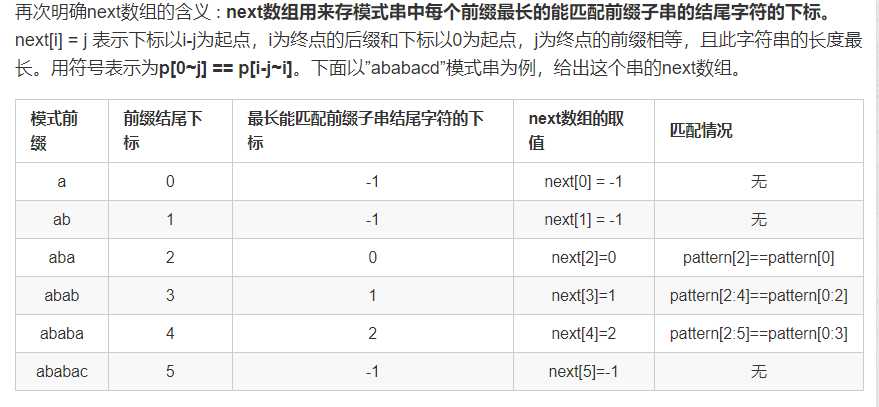
next数组本质:next[ i ] = j 表示下标以 i - j 为起点,i为终点的后缀和下标以0为起点,j为终点的前缀相等。
复制一些别人的图片用来帮助理解next是什么。
然后是kmp算法的思想原理:
下图是主串为:ababaeaba 字串为:ababacd 的一个例子;

例题:

代码:
#include<iostream> using namespace std; const int N = 1000010; //a[]是主串,b[]是模式串,在a[]中寻找b[] char a[N],b[N]; //ne[]是next数组,由于c++中存在next关键字,所以我们为了避免编译错误,起名ne[] int ne[N]; //n是主串长度,n是子串(模式串)长度 int n,m; //预处理ne数组 void prekmp(){ //模板串长度为1时无前后缀,所以循环从2开始 for(int i = 2,j = 0;i <= m ;i++){ //如果刚开始开始匹配或者匹配失败,就返回上一层匹配 while( j && b[i] != b[j+1]) j = ne[j]; //如果匹配成功 if(b[i] == b[j+1]) j++; //由于本题要输出全部匹配成功后的位置,所以我们匹配成功一个后,仍然需要回退next数组 ne[i] = j; } } void kmp(){ //开始kmp for(int i = 1,j = 0; i <= n; i++){ while(j && a[i]!=b[j+1]) j = ne[j]; if(a[i] == b[j+1]) j++; //匹配成功,输出起始下标,也就是匹配成功的终点i-模式串长度m=匹配成功的起点 if(j == m){ printf("%d ", i - m); j = ne[j]; } } } int main(){ //读入模式串 //下面那行是用c++读入的方式 //cin>>m>>b+1>>n>>a+1; //b[1]和a[1]是为了保证数据读入进来时下标从1开始存放 scanf("%d%s%d%s", &m,&b[1],&n,&a[1]); prekmp(); //kmp kmp(); return 0; }
标签:bsp pac color return i++ using 关键字 main 最大
原文地址:https://www.cnblogs.com/Flydoggie/p/12259502.html