标签:左移 不能 nlogn for循环 inf main image 场景 调用
采用Java代码描述
我们通常说到的时间复杂度是指渐进时间复杂度,其定义为:
若存在函数f(n),当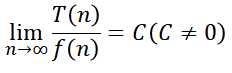 ,其中C是不为零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),则称O(f(n))为算法的渐进时间复杂度,简称时间复杂度。
,其中C是不为零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),则称O(f(n))为算法的渐进时间复杂度,简称时间复杂度。
先记住如下常见的时间复杂度之间的关系:O(1) < O(logn) < O(n) < O(nlogn) < O(n2)。
简单的说,时间复杂度是执行算法所需要的时间成本,空间复杂度是执行算法所需要的空间成本。同理,空间复杂度的计算公式记作:S(n)=O(f(n)),n为问题的规模。递归算法的空间复杂度和递归深度成正比。
二、数组
数组的特点:
1、数组中的每个元素都有自己的下标,下标从0开始,到数组长度-1结束;
2、数组中的值在内存中顺序存储;
下面就是我自己写的数组的增删改查以及扩容,打印操作的代码:
package dataStructure.MyArray;
public class MyArray {
private int[] array;
private int size;
//构造方法
public MyArray(int capacity) {
this.array = new int[capacity];
size = 0;
}
/**
*
* @Description 向数组中增加元素
* @param element 增加的元素的值
* @param index 要在哪个位置增加元素
*/
public void insert(int index, int element) {
// 判断要插入的元素的下标是否合法
if (index < 0 || index > size) {
throw new IndexOutOfBoundsException("输入的下标不合法");
}
// 判断已有的元素个数是否达到数组容量的最大值,如果达到,则进行扩容
if (size >= array.length) {
reNewArray();
}
// 进行插入操作,将要插入位置的右边的元素全部向后移动一个位置。
// 如果从插入位置开始移动,会覆盖掉右边的值,
//所以只能从最后一个元素开始,从右往左逐个的向后移动一个位置
for (int i = size - 1; i >= index; i--) {
array[i + 1] = array[i];
}
array[index] = element;
// 添加成功以后要改变数组的总个数
size++;
}
/**
*
* @Description 删除数组中指定位置的元素
* @param index 要删除元素的下标
* @return 返回要删除的元素的值
*/
public int delete(int index) {
// 判断要删除的元素的下标是否合法
if (index < 0 || index > size) {
throw new IndexOutOfBoundsException("输入的下标不合法");
}
//这里要先把要删除的元素的值取出来,
//注意不能直接返回,不然会提前结束调用
int element = array[index];
//然后将该值之后的元素往左移动一位,
//来覆盖掉这个值,达到删除效果
for(int i = index; i < size - 1; i++) {
array[i] = array[i+1];
}
//删除之后将数组的个数减1
size--;
return element;
}
/**
*
* @Description 更改数组中某个位置的值
* @param index 要改的位置
* @param element 要改成多少值
* 这个方法其实可以不需要,为了美观才写的
*/
public void update(int index, int element) {
array[index] = element;
}
/**
*
* @Description 查询数组中某个位置的值
* @param index 要查询的位置
* @return 返回要查询的位置的值
*/
public int getData(int index) {
return array[index];
}
/**
*
* @Description 扩容的方法reNewArray(),扩容为原来的两倍
*/
public void reNewArray() {
int[] newArray = new int[array.length * 2];
// 调用arraycopy()方法将原来的数组元素复制到新的数组中
System.arraycopy(array, 0, newArray, 0, array.length);
// 将新的数组的引用赋值给原来的数组
array = newArray;
}
/**
*
* @Description 打印数组中得每个元素得值
*/
public void printArray() {
for(int i = 0; i < size; i++) {
if(i == size - 1) {
System.out.println(array[i] + ";");
}else {
System.out.print(array[i] + "、");
}
}
}
public static void main(String[] args) {
MyArray myArray = new MyArray(4);
//数组中的下标从0开始
myArray.insert(0,8);
myArray.insert(1,9);
myArray.insert(2,5);
myArray.insert(3,6);
//别忘了我们有一个扩容操作
myArray.insert(4,1);
myArray.insert(5,7);
myArray.printArray();
//看看删除两个同一下标得元素值是否一样
int delete1 = myArray.delete(3);
System.out.println(delete1);
int delete2 = myArray.delete(3);
System.out.println(delete2);
//再看看现在下标为3得位置的值是多少
System.out.println(myArray.getData(3));
//更改其下标为3的值,再看看值是多少
myArray.update(3, 10);
System.out.println(myArray.getData(3));
myArray.printArray();
}
}
由代码量也可以看出,数组的查和改操作非常简单,一般都不用封装成方法。
也正是因为如此, 适合使用数组的场景是:读操作多、写操作少的场景。
插入操作:数组扩容和移动元素都只有一层for循环,所以其时间复杂度为O(n),综合起来是O(n);
删除操作、打印操作:也只有一层for循环,时间也复杂度是O(n);
查和改操作:没有循环,时间复杂度为O(1);
以上就是本期数据结构的全部内容了,欢迎大家查看交流。
我是学渣很忙,专业知识不过硬的学渣,难免会出差错,也欢迎大家批评指正!
标签:左移 不能 nlogn for循环 inf main image 场景 调用
原文地址:https://www.cnblogs.com/xzhm/p/12266512.html