标签：等于 运算 准备 就是 添加 int 最大 sel hub
时间复杂度 O(n²) 。额外空间复杂度O(1)。
比较相邻的元素。如果第一个比第二个大，就交换他们两个。
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
针对所有的元素重复以上的步骤，除了最后一个。
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。
当输入的数据已经是正序时，时间复杂度 O(n) 。
当输入的数据是反序时，时间复杂度 O(n²) 。
1 function bubbleSort(arr) { 2 var len = arr.length; 3 for (var i = 0; i < len - 1; i++) { 4 for (var j = 0; j < len - 1 - i; j++) { 5 if (arr[j] > arr[j+1]) { // 相邻元素两两对比 6 var temp = arr[j+1]; // 元素交换 7 arr[j+1] = arr[j]; 8 arr[j] = temp; 9 } 10 } 11 } 12 return arr; 13 }
选择排序是一种简单直观的排序算法，无论什么数据进去都是 O(n²) 的时间复杂度。额外空间复杂度O(1)。
所以用到它的时候，数据规模越小越好。
首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
重复第二步，直到所有元素均排序完毕。
1 function selectionSort(arr) { 2 var len = arr.length; 3 var minIndex, temp; 4 for (var i = 0; i < len - 1; i++) { 5 minIndex = i; 6 for (var j = i + 1; j < len; j++) { 7 if (arr[j] < arr[minIndex]) { // 寻找最小的数 8 minIndex = j; // 将最小数的索引保存 9 } 10 } 11 temp = arr[i]; 12 arr[i] = arr[minIndex]; 13 arr[minIndex] = temp; 14 } 15 return arr; 16 }
时间复杂度 O(n²) 。额外空间复杂度O(1)。
将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）
当输入的数据已经是正序时，时间复杂度O(n)。额外空间复杂度O(1)。
当输入的数据是反序时，时间复杂度O(n²)。额外空间复杂度O(1)。
1 function insertionSort(arr) { 2 var len = arr.length; 3 var preIndex, current; 4 for (var i = 1; i < len; i++) { 5 preIndex = i - 1; 6 current = arr[i]; 7 while(preIndex >= 0 && arr[preIndex] > current) { 8 arr[preIndex+1] = arr[preIndex]; 9 preIndex--; 10 } 11 arr[preIndex+1] = current; 12 } 13 return arr; 14 }
时间复杂度是 O(nlogn) 。额外空间复杂度O(1)。
选择一个增量序列 t1，t2，……，tk，其中 ti > tj, tk = 1；
按增量序列个数 k，对序列进行 k 趟排序；
每趟排序，根据对应的增量 ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。
1 function shellSort(arr) { 2 var len = arr.length, 3 temp, 4 gap = 1; 5 while(gap < len/3) { //动态定义间隔序列 6 gap =gap*3+1; 7 } 8 for (gap; gap > 0; gap = Math.floor(gap/3)) { 9 for (var i = gap; i < len; i++) { 10 temp = arr[i]; 11 for (var j = i-gap; j >= 0 && arr[j] > temp; j-=gap) { 12 arr[j+gap] = arr[j]; 13 } 14 arr[j+gap] = temp; 15 } 16 } 17 return arr; 18 }
时间复杂度是 O(nlogn) 。（Master公式算出）
额外空间复杂度O(n)。
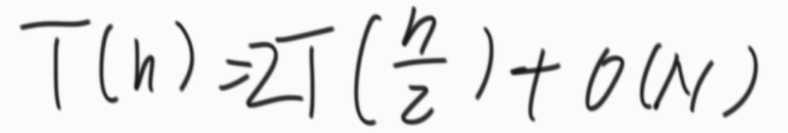
申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
设定两个指针，最初位置分别为两个已经排序序列的起始位置；
比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
重复步骤 3 直到某一指针达到序列尾；
将另一序列剩下的所有元素直接复制到合并序列尾。
1 function mergeSort(arr) { // 采用自上而下的递归方法 2 var len = arr.length; 3 if(len < 2) { 4 return arr; 5 } 6 var middle = Math.floor(len / 2), 7 left = arr.slice(0, middle), 8 right = arr.slice(middle); 9 return merge(mergeSort(left), mergeSort(right)); 10 } 11 12 function merge(left, right) 13 { 14 var result = []; 15 16 while (left.length && right.length) { 17 if (left[0] <= right[0]) { 18 result.push(left.shift()); 19 } else { 20 result.push(right.shift()); 21 } 22 } 23 24 while (left.length) 25 result.push(left.shift()); 26 27 while (right.length) 28 result.push(right.shift()); 29 30 return result; 31 }
技巧：位运算比算数运算快
①
②
随机快排的时间复杂度：O(nlogn)。随机快排的额外空间复杂度：O(logn)，空间浪费在记录大于or小于部分的划分点，最坏O(n)。随机快排的复杂度是个概率事件。
①从数列中挑出一个元素，称为 "基准"（pivot）;
经典快排：数列的最后一个数作为基准数x，≤x的放到x左边，＞x的放到x右边。小于x和大于x的部分再分别进行快排，以此类推，直到全部有序。
经典快排存在的问题：划出的小于区域和等于区域可能不会是等规模的。如果总拿最后一个数作为基准，排序的效率就与数据状况有很大的关系，
假如数列本来就是有序的，这样每次排序只能搞定一个数，最差时时间复杂度会变为O(n²)。好的情况，选择的基准数总是恰好在中间，时间复杂度为O(nlogn)。
随机快排：随机选择一个数与数列最后一个数交换，作为基准数x，＜x的放到x左边，＝x的放中间，＞x的放到x右边。利用荷兰国旗问题的方法来改进，
用随机的数来最为划分值，复杂度是一个概率事件，不能用最差来估计，而是长期情况的期望。用随机来打乱数据的状况。小于x和大于x的部分再分别
进行随机快排，以此类推，直到全部有序。随机快排是最常用的排序算法。
②重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
③递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；
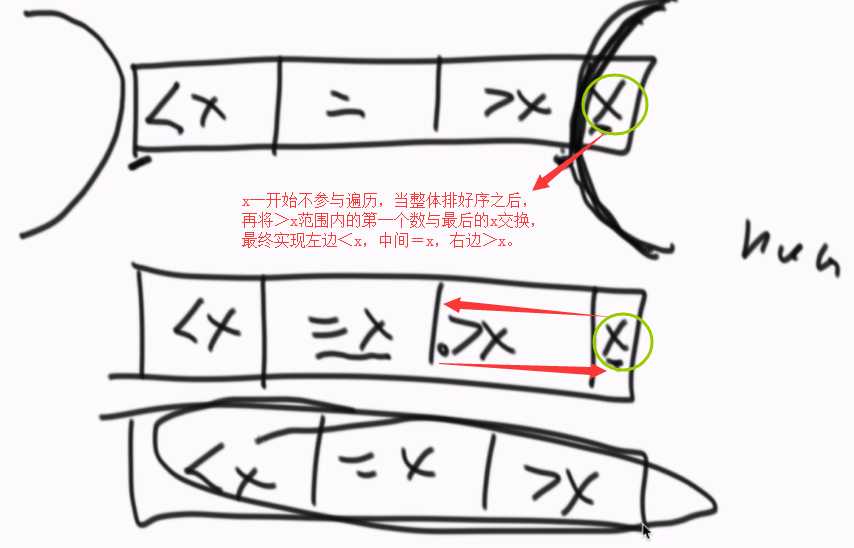这样可以省一个变量。
1 function quickSort(arr, left, right) { 2 var len = arr.length, 3 partitionIndex, 4 left = typeof left != ‘number‘ ? 0 : left, 5 right = typeof right != ‘number‘ ? len - 1 : right; 6 7 if (left < right) { 8 partitionIndex = partition(arr, left, right); 9 quickSort(arr, left, partitionIndex-1); 10 quickSort(arr, partitionIndex+1, right); 11 } 12 return arr; 13 } 14 15 function partition(arr, left ,right) { // 分区操作 16 var pivot = left, // 设定基准值（pivot） 17 index = pivot + 1; 18 for (var i = index; i <= right; i++) { 19 if (arr[i] < arr[pivot]) { 20 swap(arr, i, index); 21 index++; 22 } 23 } 24 swap(arr, pivot, index - 1); 25 return index-1; 26 } 27 28 function swap(arr, i, j) { 29 var temp = arr[i]; 30 arr[i] = arr[j]; 31 arr[j] = temp; 32 } 33 function partition2(arr, low, high) { 34 let pivot = arr[low]; 35 while (low < high) { 36 while (low < high && arr[high] > pivot) { 37 --high; 38 } 39 arr[low] = arr[high]; 40 while (low < high && arr[low] <= pivot) { 41 ++low; 42 } 43 arr[high] = arr[low]; 44 } 45 arr[low] = pivot; 46 return low; 47 } 48 49 function quickSort2(arr, low, high) { 50 if (low < high) { 51 let pivot = partition2(arr, low, high); 52 quickSort2(arr, low, pivot - 1); 53 quickSort2(arr, pivot + 1, high); 54 } 55 return arr; 56 }
满二叉树：除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树。层数为K，且结点总数是(2^k) -1
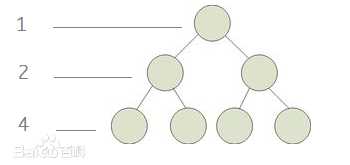
堆结构可以理解为一颗完全二叉树：对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
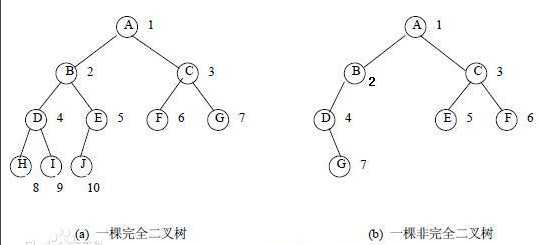
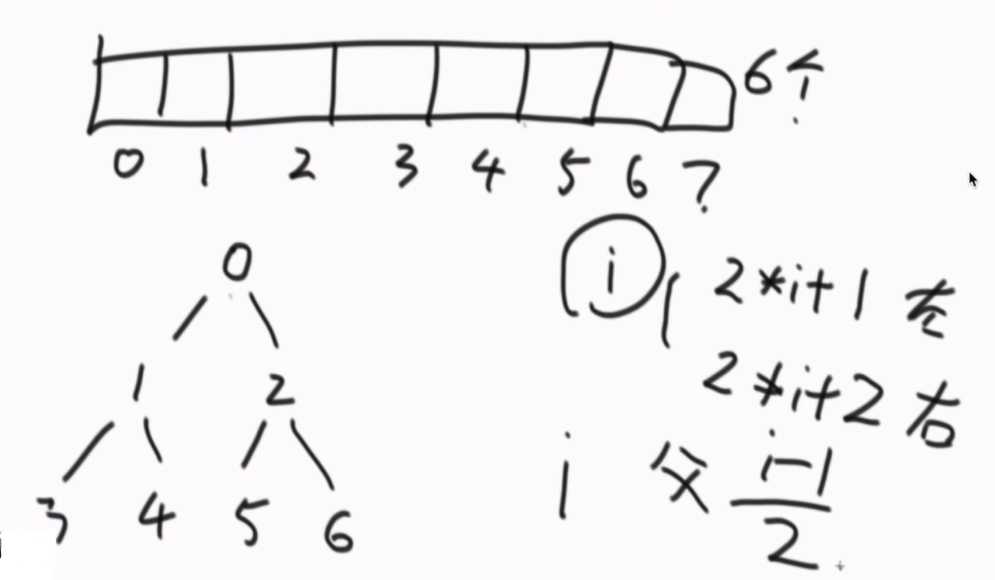用数组结构可以模拟完全二叉树。
大根堆：
在一棵完全二叉树中，任何一颗子树的最大值都是头部。
建立大根堆：
①heapInsert：给定一个数组0~n-1，给定i位置，i从0开始，依次让0~i位置形成大根堆，i++，直到所有数都插入数组中。时间复杂度O(n)。（log1+log2 + ···+ log(n-1)）收敛于n。
新增的值逐渐往上调整。
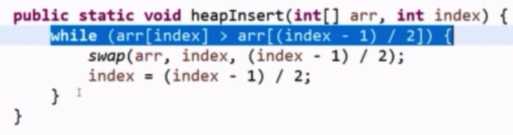在计算机中-1/2 = 0
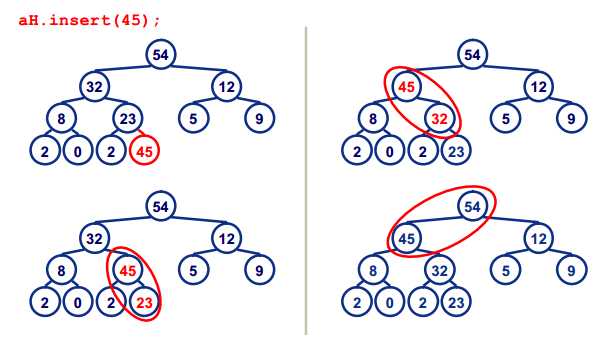
②heapify：如果数组中的某个数变了，怎么重新建立大根堆?
变化的值逐渐往下调整。
改变的数x与其最大的孩子交换，x往下沉，变到与其交换的孩子的位置，此时在与其两个孩子比较，与最大的孩子交换，x继续往下沉，直到沉到它没有孩子结束。
例如：下面大根堆中的6变成了1
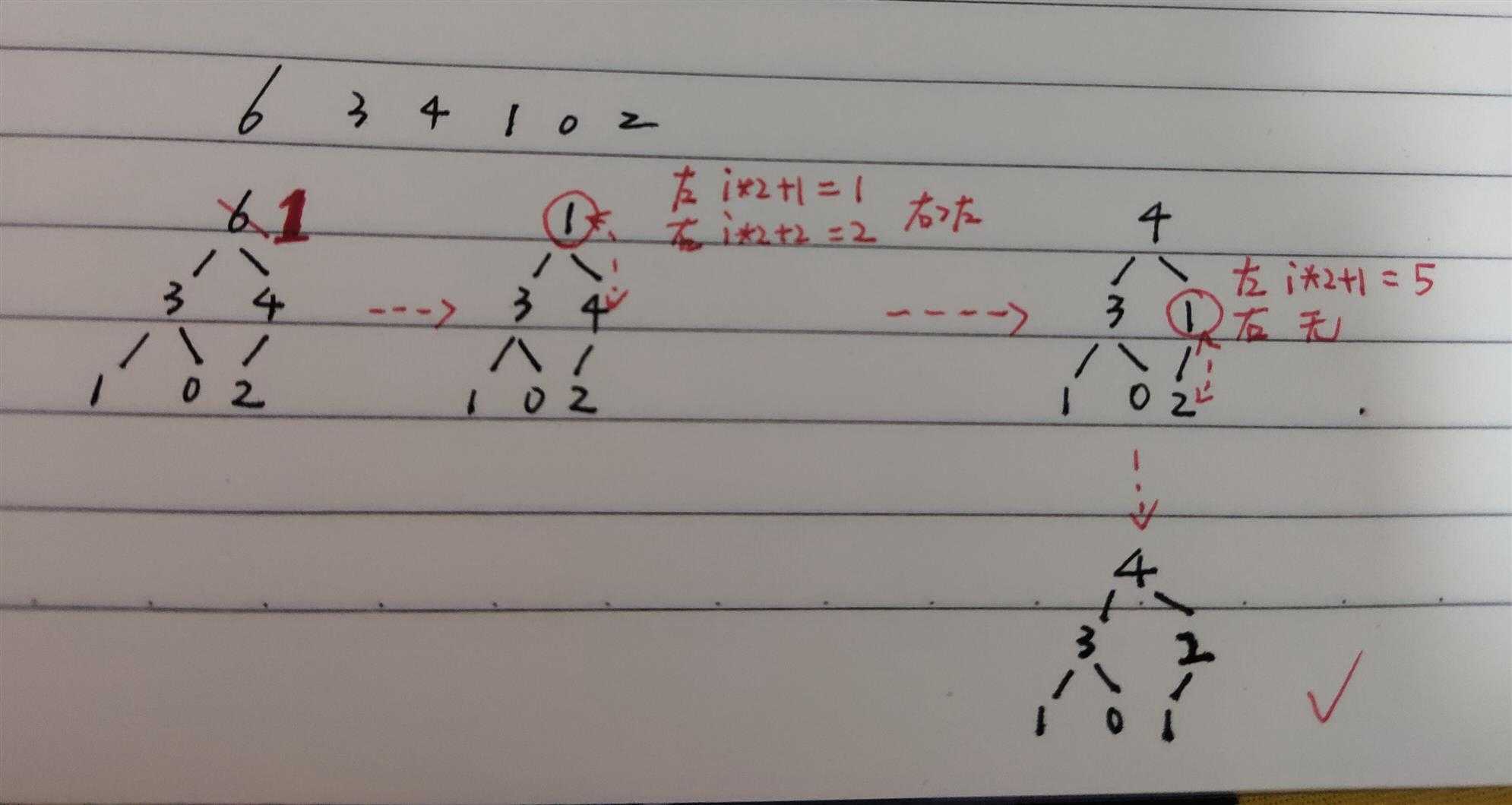
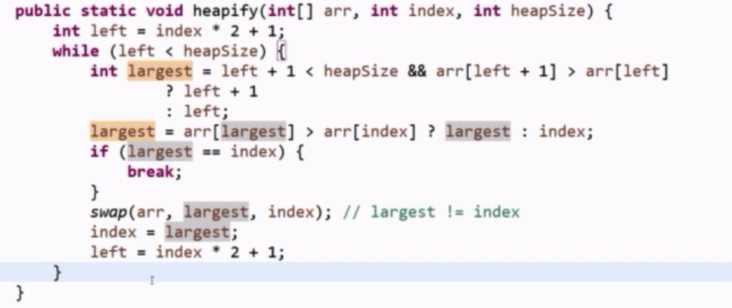
当整个完全二叉树的大小是整个数组的时候，heapsize就是数组的大小；当建立0~i范围的堆时，heapsize的大小就是0~i上数组的大小。
小根堆：
任何一颗子树中，父节点的值小于或等于子节点的值。
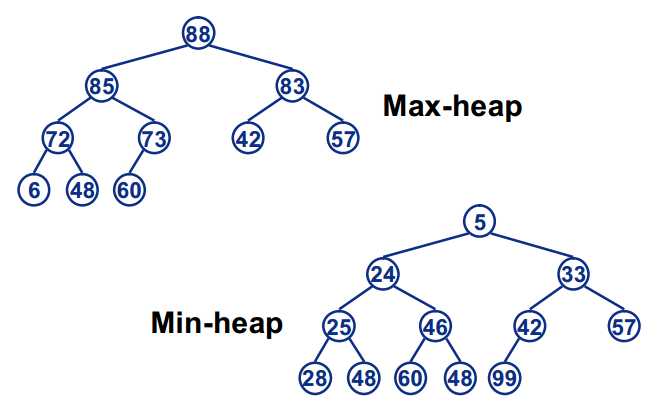
例题：
一个容器不断向外吐数，要求实现一个算法，可以随时得到已经吐出的数中的中位数。（中位数：按顺序排列的一组数据中居于中间位置的数）
思路：
准备一个大根堆数组和一个小根堆数组。吐出的第一个数放入大根堆数组建立大根堆；吐出的第二个数如果小于等于大根堆头部的数则放入大根堆输入，建立新的大根堆，否则放入小根堆数组建立小根堆；····以此类推，一旦发现大根堆与小根堆不平衡（heapsize相差＞1），就将多的那个堆的堆顶数拿出来放到小的那个堆中（例如：大根堆层数偏大，就将大根堆的堆顶数与大根堆中最后一个数交换，heapsize-1，剩下的数重新建立大根堆，最后一个数自动失效（虽然还在数组中，但不在堆中），将大根堆堆顶的数添加到小根堆中，重新建立小根堆），·······以此类推，直到所有的数都放置完毕。
大根堆中的数是较小的n/2个数，堆顶是较小的n/2个数中的最大数；小根堆中的数是较大的n/2个数，堆顶是较大的n/2个数中的最小数；因此中位数就是
1 var len; // 因为声明的多个函数都需要数据长度，所以把len设置成为全局变量 2 3 function buildMaxHeap(arr) { // 建立大顶堆 4 len = arr.length; 5 for (var i = Math.floor(len/2); i >= 0; i--) { 6 heapify(arr, i); 7 } 8 } 9 10 function heapify(arr, i) { // 堆调整 11 var left = 2 * i + 1, 12 right = 2 * i + 2, 13 largest = i; 14 15 if (left < len && arr[left] > arr[largest]) { 16 largest = left; 17 } 18 19 if (right < len && arr[right] > arr[largest]) { 20 largest = right; 21 } 22 23 if (largest != i) { 24 swap(arr, i, largest); 25 heapify(arr, largest); 26 } 27 } 28 29 function swap(arr, i, j) { 30 var temp = arr[i]; 31 arr[i] = arr[j]; 32 arr[j] = temp; 33 } 34 35 function heapSort(arr) { 36 buildMaxHeap(arr); 37 38 for (var i = arr.length-1; i > 0; i--) { 39 swap(arr, 0, i); 40 len--; 41 heapify(arr, 0); 42 } 43 return arr; 44 }
==========================桶排序、计数排序与基数排序==========================
桶排序、计数排序与基数排序都不是基于比较的排序，因此它们的排序情况就与被排序数据实际的数据状况有很大关系。实际中并不经常使用。
时间复杂度O(n)。额外空间复杂度O(n)。稳定。
按照数据状况设计容器，根据数据状况所属类别，将其放到相应的容器（桶）里。
当输入的数据可以均匀的分配到每一个桶中。
当输入的数据被分配到了同一个桶中。
元素分布在桶中：
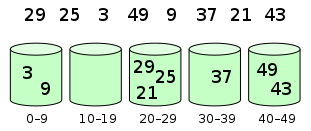
然后，元素在每个桶中排序：
function bucketSort(arr, bucketSize) {
if (arr.length === 0) {
return arr;
}
var i;
var minValue = arr[0];
var maxValue = arr[0];
for (i = 1; i < arr.length; i++) {
if (arr[i] < minValue) {
minValue = arr[i]; // 输入数据的最小值
} else if (arr[i] > maxValue) {
maxValue = arr[i]; // 输入数据的最大值
}
}
//桶的初始化
var DEFAULT_BUCKET_SIZE = 5; // 设置桶的默认数量为5
bucketSize = bucketSize || DEFAULT_BUCKET_SIZE;
var bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
var buckets = new Array(bucketCount);
for (i = 0; i < buckets.length; i++) {
buckets[i] = [];
}
//利用映射函数将数据分配到各个桶中
for (i = 0; i < arr.length; i++) {
buckets[Math.floor((arr[i] - minValue) / bucketSize)].push(arr[i]);
}
arr.length = 0;
for (i = 0; i < buckets.length; i++) {
insertionSort(buckets[i]); // 对每个桶进行排序，这里使用了插入排序
for (var j = 0; j < buckets[i].length; j++) {
arr.push(buckets[i][j]);
}
}
return arr;
}
时间复杂度O(n+k)。额外空间复杂度O(k)。
（1）找出待排序的数组中最大和最小的元素
（2）统计数组中每个值为i的元素出现的次数，存入数组C的第i项
（3）对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）
（4）反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1
理解：
按照数据状况设计容器，根据数据状况所属类别，将其放到相应的容器（桶）里。记录某种数据状况出现的次数。计数排序是对桶排序的一种实现。不适合数据量较大的情况。
例如：有一组数在0~60之间，要求给它们排序。
步骤：
1 准备一个长度为61的数组，每个位置对应0~60这些数，初始每个位置上的数都为零。
2 遍历整个数组，当前的数为i，就将数组对应i位置上的数+1，这样每个位置上的数，就是该位置的数出现的次数。
3 直到所有数都遍历完，再重新遍历整个数组，就可以还原排序好的数组。
1 function countingSort(arr, maxValue) { 2 var bucket = new Array(maxValue+1), 3 sortedIndex = 0; 4 arrLen = arr.length, 5 bucketLen = maxValue + 1; 6 7 for (var i = 0; i < arrLen; i++) { 8 if (!bucket[arr[i]]) { 9 bucket[arr[i]] = 0; 10 } 11 bucket[arr[i]]++; 12 } 13 14 for (var j = 0; j < bucketLen; j++) { 15 while(bucket[j] > 0) { 16 arr[sortedIndex++] = j; 17 bucket[j]--; 18 } 19 } 20 21 return arr; 22 }
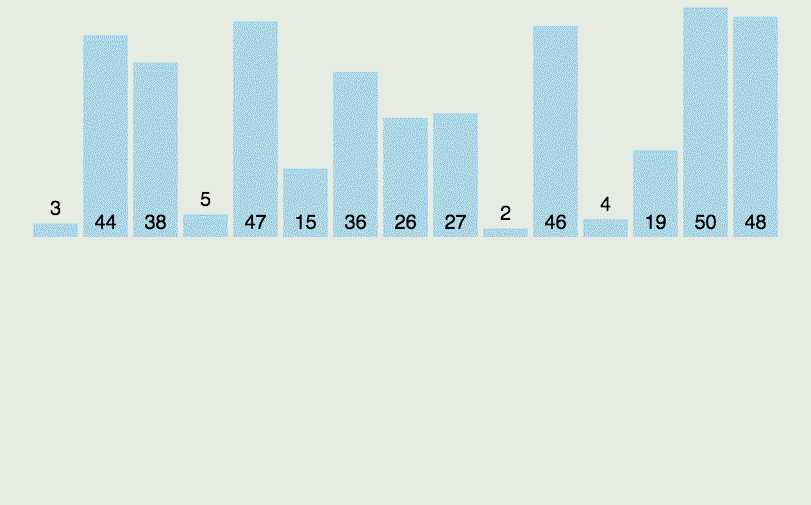
【例如】3 1 6 2 7
排序之后 1 2 3 6 7
相邻两数差值分别 1 1 3 1
最大差值为 3
【思路】
借用了桶的概念，但没有使用桶排序。
最大差值一定不来自相同桶中的数。因为：空桶左边一定存在一个离他最近的非空桶，空桶右边也一定存在一个离他最近的非空桶，这时左边非空桶中的最大值和右边非空桶中的最小值一定是相邻的，而且它们的差值一定大于这个空桶的范围。 而在相同桶内的两个数的差值一定是小于这个桶的范围的。
因此最大差值一定是来自不同桶中的两个相邻数。
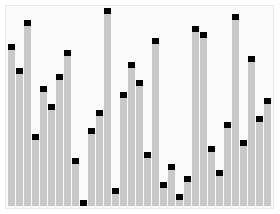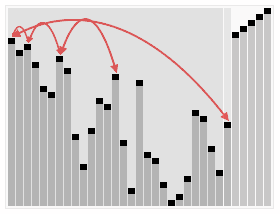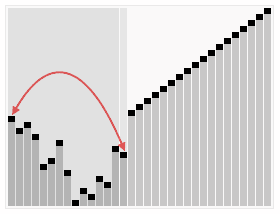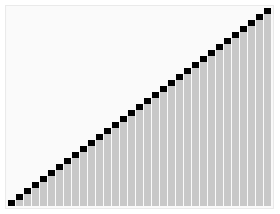
上述分析只是为了证明最大差值一定是来自不同桶中的两个相邻数，但不保证空桶左右最近的两个非空桶之间相邻数的差值是最大值！因此不能通过判断空桶周围两个非空桶之间差值来找到最大差值！如下图所示的情况可以看出。
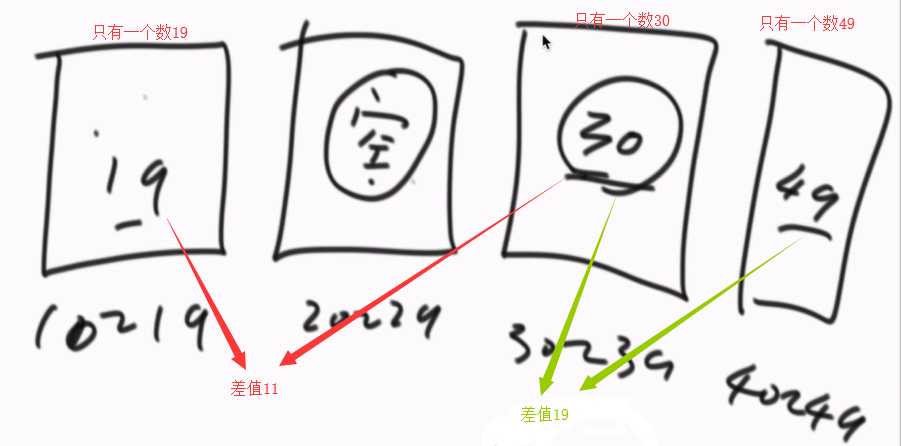
我们要通过所有非空桶和离其左边最近非空桶之间相邻数的差值来找到最大差值。
只需要记录每个桶中的最大值和最小值，以及一个布尔值bool表示该桶是否进来过数。
当一个数x开始进桶时，如果该桶的bool为false，首先将该桶的bool改为true，将最小值和最大值设置为x，如果再有数进入该桶，将其与最大值和最小值做比较，更新最大值或最小值，···以此类推，直到所有数都放置完毕。得到了各个桶的最大值和最小值，以及是否空桶的标记。
遍历各个桶，如果是空桶，进入下一个桶，直到遍历到非空桶t，再找该距离非空桶t左边最近的一个非空桶t1，计算t1的最大值与t的最小值之间的差值，···以此类推，每一非空桶都要计算其最小值与其左边最近非空桶最大值之间的差值。
最后将得到的几个差值进行比较，最大的那个即为整个数组的最大差值。
【步骤】
1 如果有n个数，就准备n+1个桶。
用3个数组来表示各个桶的三个信息。
2 遍历整个数组，找出最大值max和最小值min。
①如果最大值和最小值相等，说明整个数组都是一样的数，直接返回最大差值0。
②如果最大值和最小值不等，将最小值放到0号桶，最大值放到n号桶中；将最小值和最大值这个范围等分n+1份，其他数属于哪个范围就放到哪个桶中。
放置数的同时，还要在将其放入桶中时，将该桶的bool值改为true，表示该桶中有数了，是非空桶。并记录且不断更新每个非空桶中的最大值和最小值，
直到所有数都放置完毕。
3 遍历各个桶，如果是空桶，进入下一个桶，若是非空桶，每一非空桶都要计算其最小值与其左边最近非空桶最大值之间的差值。最后将得到的几个差值进行比较，
最大的那个即为整个数组的最大差值。
【代码实现】
1 package basic_class_01; 2 3 import java.util.Arrays; 4 5 public class Code_11_MaxGap { 6 7 public static int maxGap(int[] nums) { 8 if (nums == null || nums.length < 2) { 9 return 0; 10 } 11 int len = nums.length; 12 int min = Integer.MAX_VALUE; 13 int max = Integer.MIN_VALUE; 14 for (int i = 0; i < len; i++) { 15 min = Math.min(min, nums[i]); 16 max = Math.max(max, nums[i]); 17 } 18 if (min == max) { 19 return 0; 20 } 21 boolean[] hasNum = new boolean[len + 1]; 22 int[] maxs = new int[len + 1]; 23 int[] mins = new int[len + 1]; 24 int bid = 0; 25 for (int i = 0; i < len; i++) { 26 bid = bucket(nums[i], len, min, max); 27 mins[bid] = hasNum[bid] ? Math.min(mins[bid], nums[i]) : nums[i]; 28 maxs[bid] = hasNum[bid] ? Math.max(maxs[bid], nums[i]) : nums[i]; 29 hasNum[bid] = true; 30 } 31 int res = 0; 32 int lastMax = maxs[0]; 33 int i = 1; 34 for (; i <= len; i++) { 35 if (hasNum[i]) { 36 res = Math.max(res, mins[i] - lastMax); 37 lastMax = maxs[i]; 38 } 39 } 40 return res; 41 } 42 43 public static int bucket(long num, long len, long min, long max) { 44 return (int) ((num - min) * len / (max - min)); 45 } 46 47 // for test 48 public static int comparator(int[] nums) { 49 if (nums == null || nums.length < 2) { 50 return 0; 51 } 52 Arrays.sort(nums); 53 int gap = Integer.MIN_VALUE; 54 for (int i = 1; i < nums.length; i++) { 55 gap = Math.max(nums[i] - nums[i - 1], gap); 56 } 57 return gap; 58 } 59 60 // for test 61 public static int[] generateRandomArray(int maxSize, int maxValue) { 62 int[] arr = new int[(int) ((maxSize + 1) * Math.random())]; 63 for (int i = 0; i < arr.length; i++) { 64 arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random()); 65 } 66 return arr; 67 } 68 69 // for test 70 public static int[] copyArray(int[] arr) { 71 if (arr == null) { 72 return null; 73 } 74 int[] res = new int[arr.length]; 75 for (int i = 0; i < arr.length; i++) { 76 res[i] = arr[i]; 77 } 78 return res; 79 } 80 81 // for test 82 public static void main(String[] args) { 83 int testTime = 500000; 84 int maxSize = 100; 85 int maxValue = 100; 86 boolean succeed = true; 87 for (int i = 0; i < testTime; i++) { 88 int[] arr1 = generateRandomArray(maxSize, maxValue); 89 int[] arr2 = copyArray(arr1); 90 if (maxGap(arr1) != comparator(arr2)) { 91 succeed = false; 92 break; 93 } 94 } 95 System.out.println(succeed ? "Nice!" : "Fucking fucked!"); 96 } 97 98 }
时间复杂度O(n×k)。额外空间复杂度O(n+k)。
这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异：
1 //LSD Radix Sort 2 var counter = []; 3 function radixSort(arr, maxDigit) { 4 var mod = 10; 5 var dev = 1; 6 for (var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) { 7 for(var j = 0; j < arr.length; j++) { 8 var bucket = parseInt((arr[j] % mod) / dev); 9 if(counter[bucket]==null) { 10 counter[bucket] = []; 11 } 12 counter[bucket].push(arr[j]); 13 } 14 var pos = 0; 15 for(var j = 0; j < counter.length; j++) { 16 var value = null; 17 if(counter[j]!=null) { 18 while ((value = counter[j].shift()) != null) { 19 arr[pos++] = value; 20 } 21 } 22 } 23 } 24 return arr; 25 }
1)定义：能保证两个相等的数，经过排序之后，其在序列的前后位置顺序不变。（A1=A2，排序前A1在A2前面，排序后A1还在A2前面）
2)意义：稳定性本质是维持具有相同属性的数据的插入顺序，如果后面需要使用该插入顺序排序，则稳定性排序可以避免这次排序。
3)分类：
① 稳定性排序：冒泡排序，插入排序、归并排序、基数排序
② 不稳定性排序：选择排序、快速排序、希尔排序、堆排序
1，原地归并排序是不好的，虽然额外空间复杂度降到了O(1)，但是时间复杂度变为了 O(n²) ，得不偿失~
3，问能否做到时间复杂度 O(n)，额外空间复杂度 O(1)？很难，快排本身做不到稳定性， ”01 stable sort“可以做到，但难度很高！
如果数组很长，综合排序算法会首先判断，数组里放的是基础类型还是自己定义的类型，如果是基础类型，选择快排，如果是自己定义的类型，选择归并排序。（从稳定性出发）
如果数组很短，选择插入排序。（插入排序 常数项低，长度小于60，选择插入排序）
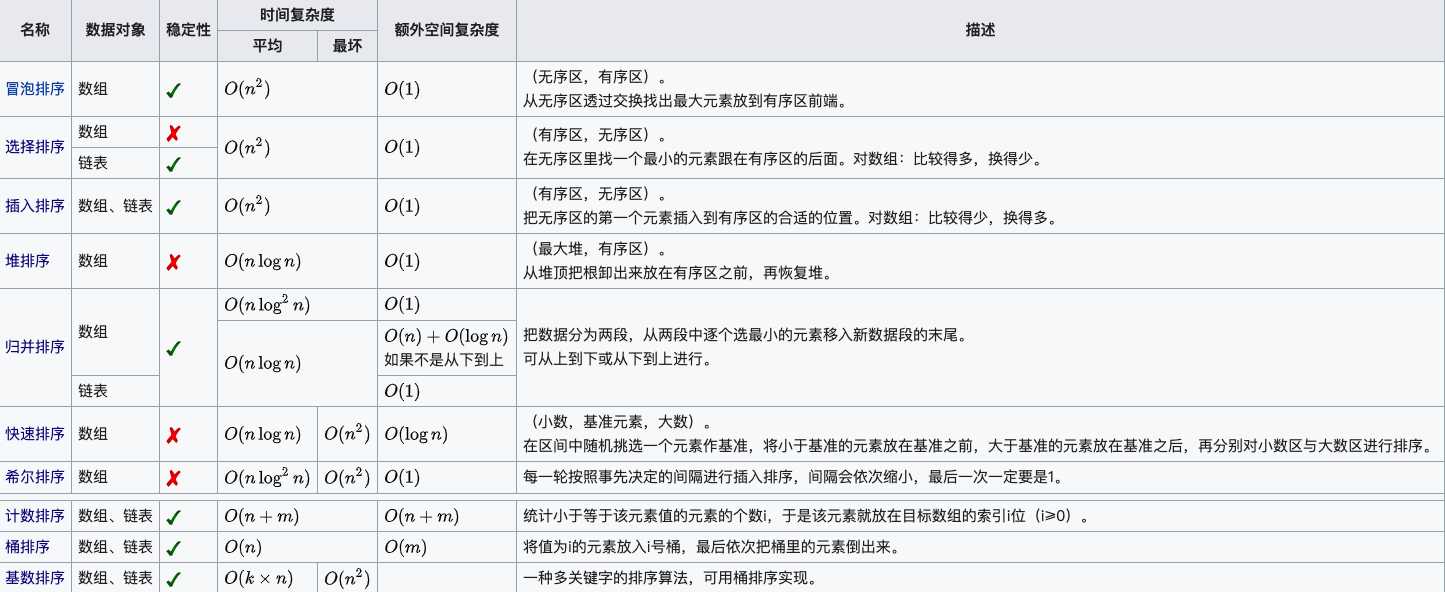
说明：
关于时间复杂度
平方阶 (O(n2)) 排序 各类简单排序：直接插入、直接选择和冒泡排序。
线性对数阶 (O(nlog2n)) 排序 快速排序、堆排序和归并排序；
O(n1+§)) 排序，§ 是介于 0 和 1 之间的常数。 希尔排序
线性阶 (O(n)) 排序 基数排序，此外还有桶、箱排序。
关于稳定性
稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序。
不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序。
名词解释
标签：等于 运算 准备 就是 添加 int 最大 sel hub
原文地址：https://www.cnblogs.com/superjishere/p/12288425.html
