标签:现在 ops void i++ 去重 ane gre 裁判 输入数据
拓扑排序的过程大概是这样的:
① 选择一个入度为0 的结点并直接输出。
② 删除这个结点以及与它关联的所有边。
③ 重复步骤①和②,直到找不到入度为0 的结点。
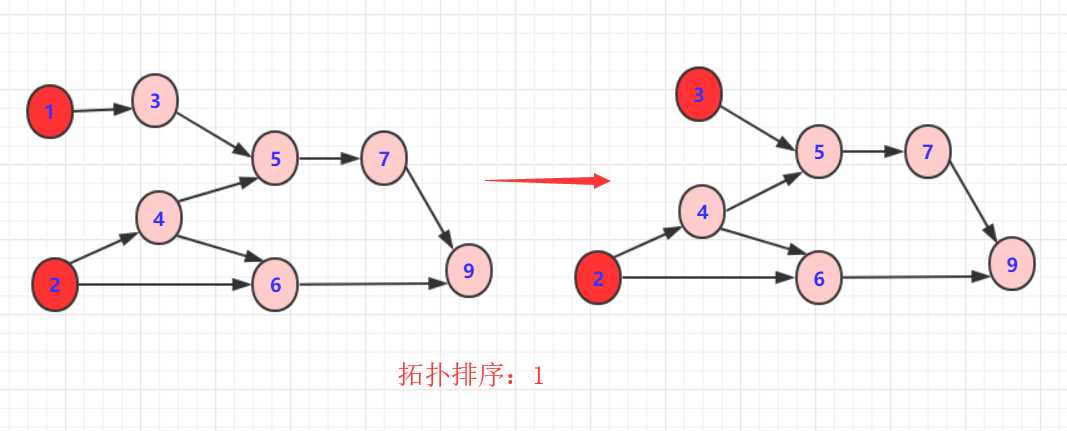
*2:删除2或3以及对应边
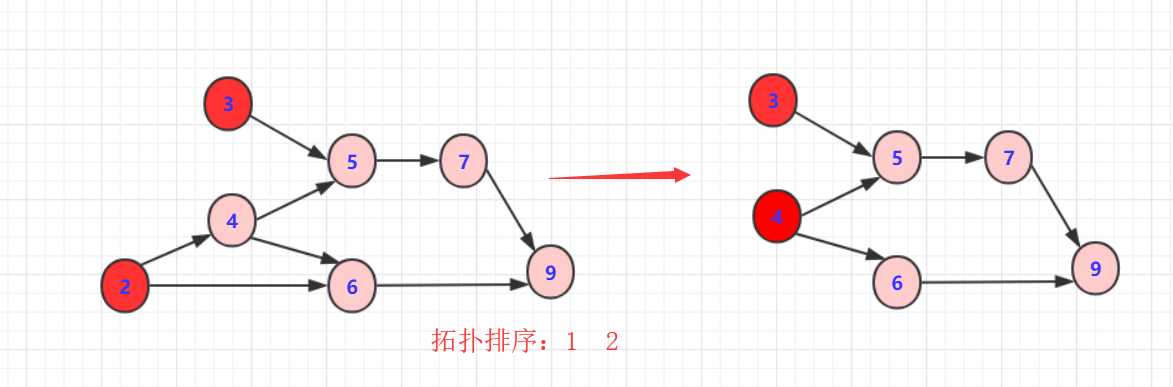
*3:删除3或者4以及对应边
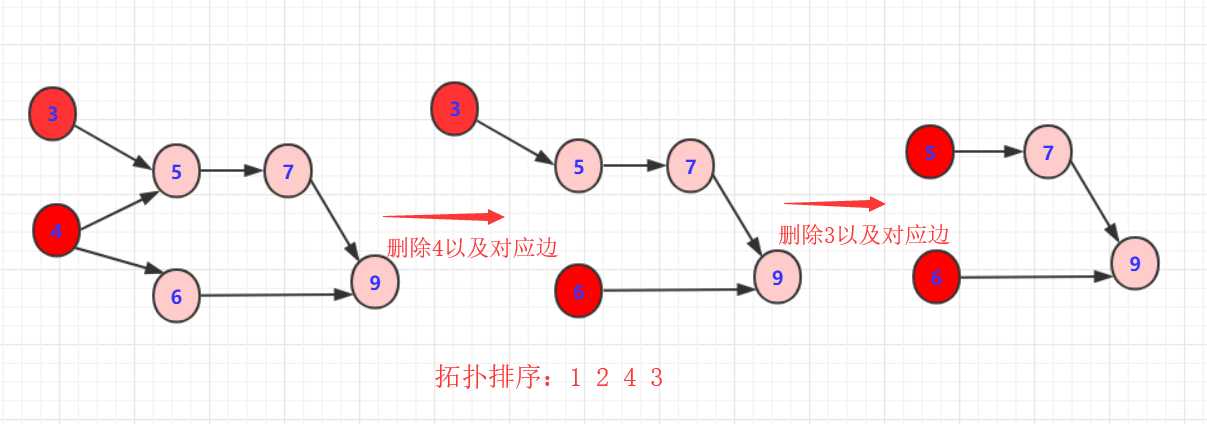
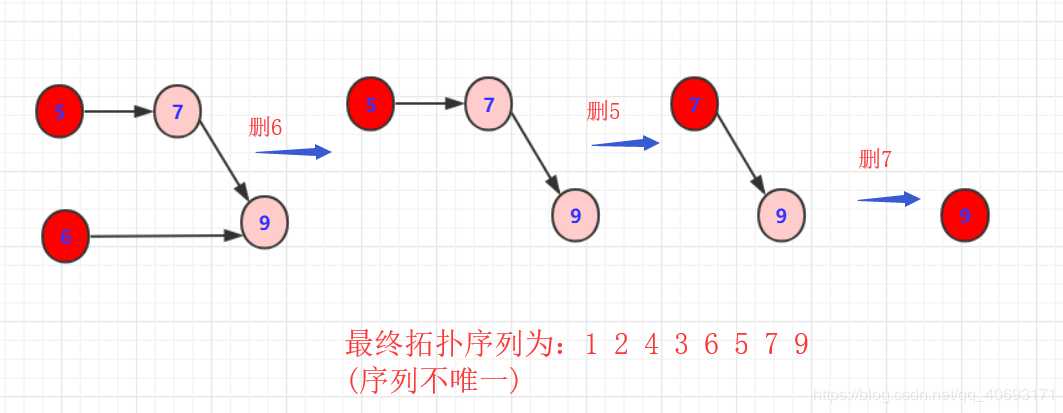
* 3:重复以上规则步骤
通过邻接矩阵来实现的代码:
1 #include<cstdio> 2 #include<cstring> 3 int ans[510][510];///邻接矩阵,记录二者是否有关联 4 int n,indegree[510];///记录节点个数 5 int queue[510];///保存拓扑 6 void topsort() 7 { 8 int i,j,top,k=0; 9 for(j=0; j<n; ++j)///遍历n次 10 { 11 for(i=1; i<=n; ++i) 12 { 13 if(indegree[i]==0)///找到入度为0的节点 14 { 15 top=i; 16 break; 17 } 18 } 19 queue[k++]=top;///当前第一名入队列,也可以直接输出 20 indegree[top]=-1;///该节点的入度更新为-1,避免重复入队列 21 for(i=1; i<=n; ++i) 22 { 23 if(ans[top][i])///删除与该店关联的边 24 indegree[i]--; 25 } 26 } 27 for(i=0; i<k-1; ++i) 28 printf("%d ",queue[i]); 29 printf("%d\n",queue[n-1]); 30 } 31 32 int main() 33 { 34 int i,a,b,m; 35 while(scanf("%d%d",&n,&m)!=EOF) 36 { 37 memset(indegree,0,sizeof(indegree));///数组初始化为0 38 memset(ans,0,sizeof(ans));///数组初始化为0 39 for(i=0; i<m; ++i) 40 { 41 scanf("%d%d",&a,&b); 42 if(ans[a][b]==0) 43 { 44 ans[a][b]=1;///二者有关联 45 indegree[b]++;///记录前驱数量 46 } 47 } 48 topsort(); 49 } 50 return 0; 51 }
接下来是一道例题:
1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <string.h> 4 #define V 510 5 int G[V][V]; //图 6 int degree[V]; //记录各顶点的入度 7 void topological_sort(int n) 8 { 9 int i, j, k; 10 for(i = 1; i <= n; i++){ 11 for(j = 1; j <= n; j++){ 12 if(degree[j] == 0){ //找到入度为0的顶点 13 printf("%d", j); //输出 14 degree[j]--; //将其入度减为-1 15 k = j; //用k记录此顶点 16 break; 17 } 18 } 19 for(j = 1; j <= n; j++){ 20 if(G[k][j] == 1){ //找到被此顶点打败过的顶点 21 G[k][j] = 0; //标记 22 degree[j]--; //将找到的顶点的入度减一 23 } 24 } 25 if(i != n) 26 printf(" "); 27 else 28 printf("\n"); 29 } 30 } 31 int main(){ 32 int n; 33 int m; 34 while(scanf("%d%d", &n, &m) != EOF){ 35 memset(G, 0, sizeof(G)); //图的初始化 36 memset(degree, 0, sizeof(degree)); //顶点入度的初始化 37 while(m--){ 38 int u, v; 39 scanf("%d%d", &u, &v); //u打败了v 40 if(G[u][v] == 0){ /*去重这里要记录的是v被多少人打败过 */ 41 G[u][v] = 1; //u打败过v 42 degree[v]++; //顶点v的入度加一 43 } 44 } 45 topological_sort(n); 46 } 47 return 0; 48 }
标签:现在 ops void i++ 去重 ane gre 裁判 输入数据
原文地址:https://www.cnblogs.com/very-beginning/p/12296018.html