标签:_id 成绩 实现 理解 不难 二分 时间 sort arrays
成绩不是很好,代码本身写的也很乱,本文只是提供一种解题思路。
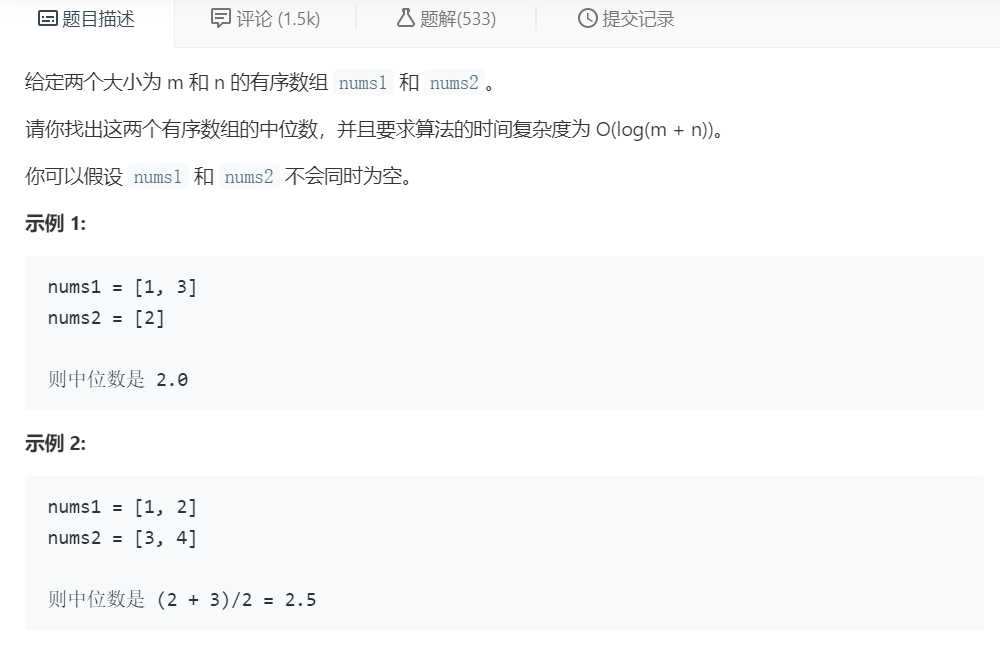
要求两有序数组的中位数并不难,简单粗暴的方法就是得到两数组合并后的新数组,取其中位数即可,但是难度在于这个时间复杂度有限制,为 O(log(m + n))。
一看这个log,那么很容易想到二分查找算法什么的,而本文的解题过程也正是按照二分的思路来的。通过每次比较两数组的二分位点,来进行中位数的筛选。
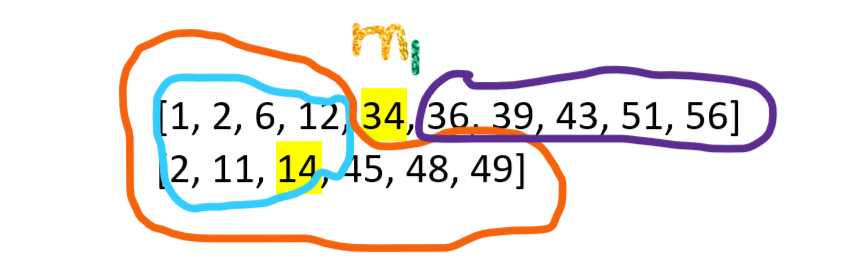
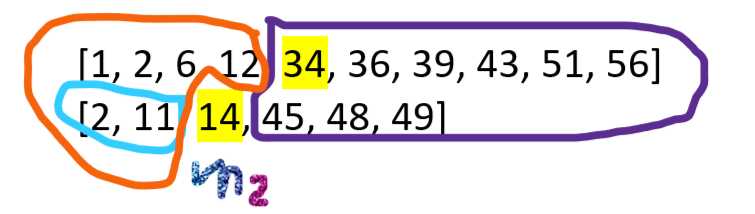
例:有两有序数组L1=[1, 2, 6, 12, 34, 36, 39, 43, 51, 56],L2=[2, 11, 14, 45, 48, 49],要求中位数 。
设L为L1和L2合并后的有序数组。那么可以看出我们要找的中位数在L中的下标应为7、8
![]()



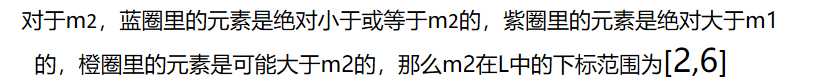

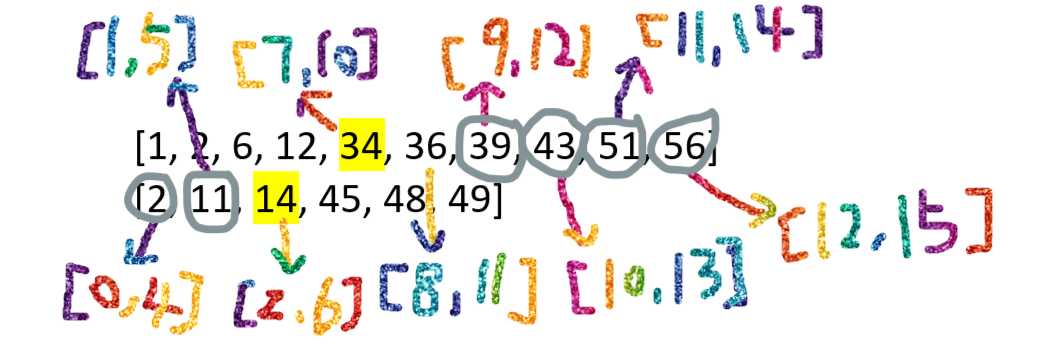
![]()


代码实现过程有点曲折,经过几次提交修修补补形成了以下这段代码,写的不太好,理解了以上的思路后大家可以自己实现。
class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
l1 = nums1
l2 = nums2
m1 = (len(l1)+len(l2))//2
m2 = (len(l1)+len(l2))/2
m_idx = [m1-1, m1] if m1 == m2 else [m1]
be_num = m1 - (len(m_idx) - 1)
af_num = be_num
while be_num > 0 and af_num > 0 and len(l1) != 0 and len(l2) != 0:
low1, high1, low2, high2 = 0, len(l1) - 1, 0, len(l2) - 1
mid1 = (low1+high1)//2
mid2 = (low2+high2)//2
if l1[mid1] < l2[mid2]:
low1 = max(min(mid1 + m_idx[0]-(mid1+mid2), len(l1)-1,mid1+1), 0)
be_num -= low1
high2 = max(min(mid2 + m_idx[-1] - (mid1 + mid2 + 1), len(l2) - 1), mid2-1)
af_num -= len(l2) - high2 - 1
else:
low2 = max(min(mid2 + m_idx[0] - (mid1 + mid2), len(l2)-1, mid2+1), 0)
be_num -= low2
high1 = max(min(mid1 + m_idx[-1] - (mid1 + mid2 + 1), len(l1) - 1), mid1-1)
af_num -= len(l1) - high1 - 1
l1 = l1[low1:high1+1]
l2 = l2[low2:high2+1]
m_idx = [be_num] if len(m_idx) == 1 else [be_num, be_num + 1]
newList = []
while len(l1) != 0 and len(l2) != 0:
if l1[0] < l2[0]:
newList.append(l1[0])
l1.remove(l1[0])
else:
newList.append(l2[0])
l2.remove(l2[0])
newList.extend(l1)
newList.extend(l2)
if be_num == 0 and af_num == 0:
newList = newList
elif be_num == 0 and af_num != 0:
newList = newList[:-af_num]
elif be_num != 0 and af_num == 0:
newList = newList[be_num:]
else:
newList = newList[be_num:-af_num]
# elif be_num == 0:
# newList = newList[:-af_num]
# elif af_num == 0:
# newList = newList[be_num+1:]
return sum(newList)/len(newList)
标签:_id 成绩 实现 理解 不难 二分 时间 sort arrays
原文地址:https://www.cnblogs.com/zhuangzi101/p/12323796.html