标签:衡量 文件结构 外部 提取 简单 mda problems 物理 经典的
数据结构与算法分析c++版
学习记录
一、绪论
1.数据结构的必要性
计算机程序被设计出来的目的不仅仅是为了计算,同时其也要完成数据的提取和检索任务,并尽可能地高效快速。在这个意义下,数据结构和算法分析作为程序的核心,就显得尤为重要。如何利用数据结构和算法,设计出简单易懂,并且高效地利用计算机资源的程序是这门课的核心议题。
Def 一个算法被称为有效的(effective),如果其能在计算机的资源限制下解决相应问题:这些限制通常包括计算机储存量限制,以及算法运行的时间限制。
算法的消耗(cost),是指该算法为解决特定问题而调动的所有资源。通常我们用时间来主要衡量一个算法的消耗。
为了降低算法的消耗量,最大化算法的效率,就要选择合适的数据结构,设计合适的算法来解决问题。因此面对一个问题,首先要确定算法要用何种方法来实现,分析其数据存储与提取方式,在此基础上确定用何种数据结构解决问题。在数据结构这个层面上,一般要考虑三个问题:
1.所有数据是一开始就要插入进数据结构里?还是在数据结构运行的过程中插入?
2.数据可否从结构中删除?
3.所有数据是否以良定义的顺序储存在结构中?或者被检索的时候能够被特定地找到?
2.ADT(Abstract Data Types)和数据结构
类(Type)是值(values)的集合,数据项(Data item)是这个集合中的元素。而一个数据类(Data Type)在实际使用中不仅仅包含类(逻辑概念),还包含附加于其上的各种操作(实际操作)。我们应该明确区分数据类型的逻辑部分和其在电脑中的实际应用。
比如计算机会通过‘数组’的形式来存储数据,这个数组就可以看作是一个类,并且我们可以通过期内元素的索引(index)来提取相应的元素,这就是数组逻辑概念。在实际的电脑储存中,电脑会为每个元素分配固定的储存位置和储存大小,这就涉及到数组的物理存储。再比如大型稀疏矩阵的存储中,计算机不会为0分配空间存储,仅仅只存非0元,这也涉及到数组物理层面的操作。
而ADT就是指一个数学模型以及定义在此数学模型上的一组操作。它通常是对数据的某种抽象,定义了数据的取值范围及其结构形式,以及对数据操作的集合。实现ADT的行为就称为数据结构(Data
Structure). 例如C++里的各种Class和int就是一个数据结构,其描述了变量的类型并且也实际地在计算机中分配了资源给变量;Maple里的各种包,包含了各种实用函数以及通用的数据也是数据结构。
数据结构强调数据要储存在计算机的主存区,与之对应的“文件结构”就可以描述外部存储器的数据结构例如光盘。
需要注意的是:ADT会描述出内部数据的类型,以及附加于其上的各种操作的结果。但并不会告诉使用者这些数据怎么来的,以及这些操作怎么运行的。换言之ADT是被封装好了的。这种性质有助于我们更好地分析处理问题。
ADT定义了Data type的逻辑形式,Data Structure定义了Data type的物理形式。
3.设计流程
设计流程:软件设计师学习和重复使用组合软件组件的模式,被称作设计流程(非常抽象的定义,个人理解其实是程序员们在设计算法的过程中,要反复调用特定语言里的各种包和函数来实现自己的目的。)或者更直接一点,就是大家都在解决问题的时候都喜欢画流程图。
有四种经典的模式:Flyweight模式;Visitor模式;Composite模式;Strategy模式
首先是Flyweight模式,其设计的初衷是运用共享技术有效地支持大量细粒度的对象。经典的例子就是:有些应用程序在整个设计过程中采用一种对象技术,比如论文的语法错误检查,其会对每个单词,甚至每个字符进行查错和处理。显然简单地实现这种技术代价极大。因为论文字数太多,庞大对象群庞大,如果对每个字符,甚至对重复的字符都进行处理的话,就会造成空间的巨大消耗,而影响性能。
实际上一篇论文的字符也无非26个,因此对重复的字符,进行共享操作处理,就可以避免重复操作带来的冗余。特别注意,Flyweight只存储相应的字符代码,而且会有内部状态和外部状态的区别:
内部状态存储于flyweight中,它包含了独立于flyweight场景的信息,这些信息使得flyweight可以被共享。如字符代码,字符大小……
外部状态取决于flyweight场景,并根据场景而变化,因此不可共享。用户对象负责在必要的时候将外部状态传递给flyweight。如字符位置,字符颜色……
适用场合:
• 一个应用程序使用了大量的对象。
• 完全由于使用大量的对象,造成很大的存储开销。
• 对象的大多数状态都可变为外部状态。
• 如果删除对象的外部状态,那么可以用相对较少的共享对象取代很多组对象。
• 应用程序不依赖于对象标识。由于Flyweight对象可以被共享,对于概念上明显有别的对象,标识测试将返回真值。
其次Visitor模式:在数据结构中保存着许多元素,我们会对这些元素进行“处理”。在Visitor模式中,数据结构与处理被分离开来。我们编写一个表示“访问者”的类来访问数据结构中的元素,并把对各元素的处理交给访问类。这样,当需要增加新的处理时,我们只需要编写新的访问者,然后让数据结构可以接受访问者的访问即可。
Visitor模式一个最基本的原则就是,可以扩展访问者类的结构,但不能修改他的。试想我们在原本的数据结构中加入了新的数据类,我们自然是希望访问者类可以更新自己并作用于新类上,而我们要做的就仅仅是在原有的“访问者”里添加扩展新的运算来适应新环境,但要是将原有的访问者类修改,要修改所有先前的类的处理方式,浪费时间而且毫无意义。
对于Composite模式,先看一个例子:
在计算机文件系统中,有文件夹的概念,文件夹里面既可以放入文件也可以放入文件夹,但是文件中却不能放入任何东西。文件夹和文件构成了一种递归结构和容器结构。虽然文件夹和文件是不同的对象,但是他们都可以被放入到文件夹里,所以一定意义上,文件夹和文件又可以看作是同一种类型的对象,所以我们可以把文件夹和文件统称为目录条目,(directory entry).在这个视角下,文件和文件夹是同一种对象。
所以,我们可以将文件夹和文件都看作是目录的条目,将容器和内容作为同一种东西看待,可以方便我们递归的处理问题,在容器中既可以放入容器,又可以放入内容,然后在小容器中,又可以继续放入容器和内容,这样就构成了容器结构和递归结构。
这就引出了的composite模式,也就是组合模式,组合模式就是用于创造出这样的容器结构的。是容器和内容具有一致性,可以进行递归操作。具体地可以参考如下的示意图
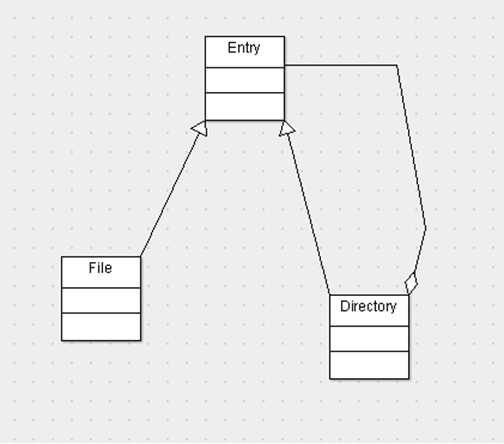
这幅图揭示了Composite模式的本质:如果我们把File看做文件夹,Directory看做文件夹,Entry就是他们的共有性质——都可以被放入文件夹内。而具有这样性质的Entry,自然又可以放入Directory里,但显然无法把文件夹放入文件里。
Strategy模式就比较好理解了:他用于算法的自由切换和扩展,它是应用较为广泛的设计模式之一。策略模式对应于解决某一问题的一个算法族,允许用户从该算法族中任选一个算法来解决某一问题,同时可以方便地更换算法或者增加新的算法。只要涉及到算法的封装、复用和切换都可以考虑使用策略模式。比较典型的例子就是Maple里的各种包,他是被封装起来的函数类:策略模式提供了对“开闭原则”的完美支持,用户可以在不修改原有系统的基础上选择算法或行为,也可以灵活地增加新的算法或行为。
4.问题,算法和程序
问题(Problems)是我们遇见的实际问题:其不应该限制用何种方式解决,但应该限制所能使用的资源。算法是解决问题的思路,也是程序的灵魂,其应该满足几个基本要求:1.要能解决问题;2.要能在有限步解决问题。3.必须是固定的步骤。
标签:衡量 文件结构 外部 提取 简单 mda problems 物理 经典的
原文地址:https://www.cnblogs.com/buka-techhome/p/12336125.html