标签:计算 gray users bsp alt 操作 tco 经典的 作品
生成逼近曲线:approxPolyDP 函数
该函数采用 Douglas-Peucker 算法(也称迭代终点拟合算法)。可以有效减少多边形曲线上点的数量,生成逼近曲线,简化后继操作。
经典的 Douglas-Peucker 算法描述如下:
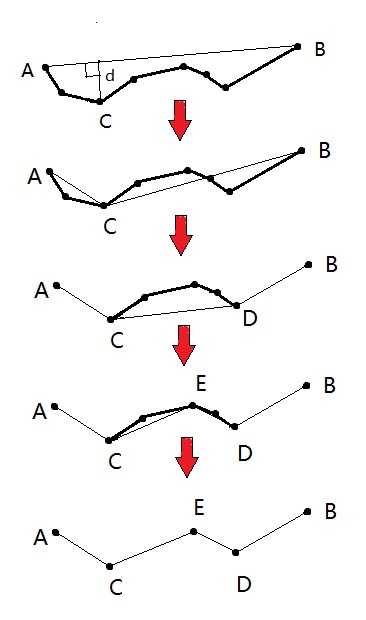
void approxPolyDP(InputArray curve, OutputArray approxCurve, double epsilon, bool closed);
代码示例:
//作品《抽象的牛》
#include<opencv.hpp> #include<iostream> using namespace cv; using namespace std; int main() { Mat src = imread("C:/Users/齐明洋/Desktop/6.jpg"); imshow("src", src); Mat gray, bin_img; cvtColor(src, gray, COLOR_BGR2GRAY); //将原图转换为灰度图 imshow("gray", gray); //二值化 threshold(gray, bin_img, 150, 255, THRESH_BINARY_INV); Mat kernel = getStructuringElement(MORPH_RECT, Size(3, 3)); morphologyEx(bin_img, bin_img, MORPH_CLOSE, kernel, Point(-1, -1), 2);//闭操作,先膨胀后腐蚀,消除小黑点 imshow("bin_img", bin_img); //寻找轮廓 vector<vector<Point> >contours; findContours(bin_img, contours, RETR_TREE, CHAIN_APPROX_NONE); //生成逼近曲线 Mat dst = Mat::zeros(src.size(), src.type()); RNG rngs = { 12345 }; vector<vector<Point> >approx_contours(contours.size());//存放逼近曲线的数组 for (int i = 0; i < contours.size(); i++) { approxPolyDP(contours[i], approx_contours[i], 40, true); Scalar colors = Scalar(rngs.uniform(0, 255), rngs.uniform(0, 255), rngs.uniform(0, 255)); drawContours(dst, approx_contours, i, colors, 3); } imshow("dst", dst); waitKey(0); }
效果演示:
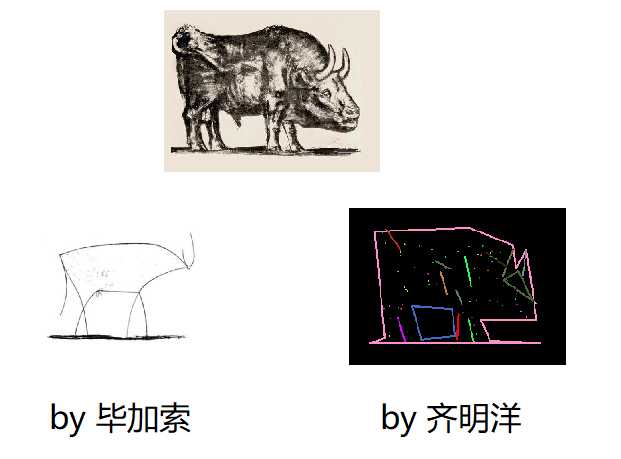
借鉴博客:https://blog.csdn.net/u013925378/article/details/86075230
标签:计算 gray users bsp alt 操作 tco 经典的 作品
原文地址:https://www.cnblogs.com/bjxqmy/p/12347265.html