标签:图解 噪声 注意 应该 过拟合 网络 模型 项目 分类
1.概念:K近邻(k-Nearest Neighbor, 简称KNN)算法是一种非常简单的机器学习监督算法。
2.主要思想:即时给定一个训练数据集,对于新的数据样本,在训练集中找到与该样本最邻近的k个样本,统计这k个样本的多数所属类,就把这个样本归结到这个所属类中。
3.根据维基百科的图解进行分析
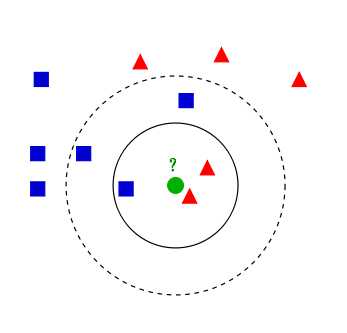
如上图所示,有红色三角形,蓝色正方形俩类数据,图中绿色的圆点代表带分类的数据,下面我们根据k近邻算法给绿色圆点进行分类
如果k=3,绿色圆点最近邻的三个点是 2红 1 蓝,结果显而易见,少数从属于多数,将绿色圆点判定为红色三角形一类
如果k=5,绿色圆点最近零的五个点是 3蓝 2红,最终将绿色圆点判定为蓝色正方形类
4.原理中涉及的问题
从上面例子我们可以看出,k近邻的算法思想非常的简单,也非常的容易理解,但是要用到项目中,还是用需要注意的,比如k怎么确定的,k为多少效果最好呢?所谓的最近邻又是如何来判断给定呢?
1.首先说明一下 k 的参数 非常难选取。
如果我们选取较小的k值,那么就会意味着我们的整体模型会变得复杂,容易发生过拟合
所谓的过拟合就是在训练集上准确率非常高,而在测试集上准确率低,经过上例,我们可以得到k太小会导致过拟合,很容易将一些噪声(如上图离五边形很近的黑色圆点)学习到模型中,而忽略了数据真实的分布!
如果我们选取较大的k值,就相当于用较大邻域中的训练数据进行预测,这时与输入实例较远的(不相似)训练实例也会对预测起作用,使预测发生错误,k值的增大意味着整体模型变得简单。
k值增大怎么就意味着模型变得简单了,我们猜想,如果k=N(N为训练样本的个数),那么无论输入实例是什么,都将简单地预测它属于在训练实例中最多的类。这时,模型是不是非常简单,这相当于你压根就没有训练模型呀!直接拿训练数据统计了一下各个数据的类别,找最大的而已。
k值既不能过大,也不能过小,那么我们一般怎么选取呢?
李航博士书上讲到,我们一般选取一个较小的数值,通常采取 交叉验证法来选取最优的k值。(也就是说,选取k值很重要的关键是实验调参,类似于神经网络选取多少层这种,通过调整超参数来得到一个较好的结果)
2.特征归一化
首先举例如下,我用一个人身高(cm)与脚码(尺码)大小来作为特征值,类别为男性或者女性。我们现在如果有5个训练样本,分布如下:
A [(179,42),男] B [(178,43),男] C [(165,36)女] D [(177,42),男] E [(160,35),女]
通过上述训练样本,很容易看到第一维身高特征是第二维脚码特征的4倍左右,那么在进行距离度量的时候,我们就会偏向于第一维特征。这样造成俩个特征并不是等价重要的,最终可能会导致距离计算错误,从而导致预测错误。
测试验证:一个测试样本 F(167,43),让我们来预测他是男性还是女性,我们采取k=3来预测。
下面我们用欧式距离分别算出F离训练样本的欧式距离,然后选取最近的3个,多数类别就是我们最终的结果,计算如下:
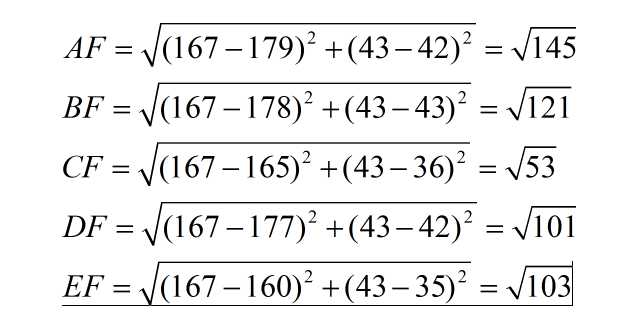
由计算可以得到,最近的前三个分别是C,D,E三个样本,那么由C,E为女性,D为男性,女性多于男性得到我们要预测的结果为女性。
这样问题就来了,一个女性的脚43码的可能性,远远小于男性脚43码的可能性,那么为什么算法还是会预测F为女性呢?那是因为由于各个特征量权重的不同,在这里导致了身高的重要性已经远远大于脚码了,这是不客观的。
所以我们应该让每个特征都是,同等重要的,这也是我们要归一化的原因。
归一化公式:

1.k近邻算法的核心思想是,即时给定一个训练数据集,对于新的数据样本,在训练集中找到与该样本最邻近的k个样本,统计这k个样本的多数所属类,就把这个样本归结到这个所属类中。
2.与该实例最近邻的k个实例,这个最近邻的定义是通过不同距离函数来定义,我们最常用的是欧式距离,还可以采用闵可夫斯基距离, 曼哈顿距离,切比雪夫距离,余弦距离等等
3.为了保证每个特征同等重要性,我们这里对每个特征进行归一化。
4.k值的选取,既不能太大,也不能太小,何值为最好,需要实验调整参数确定!
---下一篇:基于面向对象的KNN算法实现
标签:图解 噪声 注意 应该 过拟合 网络 模型 项目 分类
原文地址:https://www.cnblogs.com/cmxbky1314/p/12349564.html