标签:分组 数据 def 二叉树 说明 开始 hellip 高度 排序算法
直接插入、选择排序、冒泡排序、快速排序、……归并排序、基数排序、希尔、堆排序、
思想是:1、将数据序列分成两部分,前一部分是有序的,后面一部分是无序的.
2、将无序变有序,首先从第一开始,然后第一,第二比较后排序,此时这两位就是有序的了;然后从无序的队列中取出第三位和第二位比较,然后他们中矮的再和第一位比较,此时三位是有序的;
然后再取出第四位,和前面的比较……,一直到最后一位比较。
def insert_sort(aList): n = len(aList) for i in range(n): j = i while j > 0: if aList[j] < aList[j - 1]: aList[j], aList[j -1] = aList[j - 1], aList[j] j -= 1 if __name__ == "__main__": li = [54, 26, 93, 17, 77, 31, 44, 55, 20] insert_sort(li) print(li)
思路是:1、首先再未排序中找出最大(小)元素,存放到排序序列的起始位置;
2、再从剩余排序序列中寻找最大(小)元素,然后放到已排序序列的末尾,以此类推,知道所有元素均排序完毕;
def select_sort(aList): l = len(aList) for j in range(l): min_index = j for i in range(min_index + 1,l): if aList[min_index] > aList[i]: min_index = i # 循环一遍后找到最小的索引 aList[j], aList[min_index] = aList[min_index], aList[j] if __name__ =="__main__": li = [5, 16, 23, 19, 15, 35] select_sort(li) print(li)
思路是:1、将序列当中的左右元素依次比较,保证右边的元素始终大于左边的元素;(第一轮结束后,序列最后一个元素一定是当前序列的最大值;)
2、对序列当中剩下的n-1个元素依次遍历,(利用while循环可以减少执行次数);
def bubble_sort(aList): n = len(aList) for i in range(n - 1): for j in range(n - i - 1): if aList[j] > aList[j + 1]: aList[j], aList[j + 1] = aList[j + 1], aList[j] if __name__ == ‘__main__‘: li = [10, 22, 33, 41, 54, 55, 14] bubble_sort(li) print(li)
最优时间复杂度:O(n)(表示遍历一次发现没有任何可以交换的元素,排序结束。)
最坏时间复杂度:O(n^2)
思路是:1、从列表中找出一个元素,mid_val 作为“基准”元素.
2、然后对列表进行排序,排序的规则是,比min_val基准元素小的放在基准元素左边,比min_val基准元素大的放在基准元素的右边。这个时候基准元素就在这个列表的中间位置。这个称为分区操作。
3、递归进行操作,就是在把基准元素左边的元素当作一个列表重复步骤2的操作,把基准元素右边的元素当作一个列表重复第2步操作;
快速排序实现①
def quick_sort(arr): if len(arr)<=1: return arr pivot = arr[len(arr)//2] left = [x for x in arr if x < pivot] middle = [x for x in arr if x == pivot] right = [x for x in arr if x > pivot] return quick_sort(left) + middle + quick_sort(right) if __name__ == "__main__": li = [10, 22, 33, 41, 54, 55, 14, 57] print(quick_sort(li))
快速排序实现②
def quicksort(nums): if len(nums) <= 1: return nums left =[] right = [] base = nums.pop() for x in nums: if x < base: left.append(x) else: right.append(x) return quicksort(left) + [base] + quicksort(right) if __name__ == ‘__main__‘: nums = [21, 63, 23, 73, 2, 4, 58, 39, 29, 18] print(quicksort(nums))
堆排序:
基本思想:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点.将其与末尾元素进行交换,此时末尾就为最大值.然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值.如此反复执行,便能的带一个有序序列.
时间复杂度:
堆排序的时间复杂度分为两个部分一个是建堆的时候所耗费的时间,一个是进行堆调整的时候所耗费的时间.建堆是一个线性过程,相当于o(h1)+o(h2)+…+o(hlen/2)这里h表示节点深度,len/2表示节点最大深度,对于求和过程,结果都是线性O(n).堆调整为一个递归的过程,调整堆的过程时间复杂度与堆的深度有关系,相当于lgn的操作.
因为建堆的时间复杂度是O(n),调整堆的时间复杂度是O(lgn),所以堆排序的时间复杂度是O(nlgn).
def heap_adjust(array, start, end):
temp = array[start]
child = 2 * start
while child <= end:
if child < end and array[child] < array[child + 1]:
child += 1
if temp >= array[child]:
break
array[start] = array[child]
start = child
child *= 2
array[start] = temp
def heap_sort(array):
# 从最后一个有孩子节点的节点开始调整最大堆
first = len(array) // 2 - 1
for start in range(first, -1, -1):
heap_adjust(array, start, len(array) - 1)
# 将最大的堆放在堆的最后一个位置,并继续调整排序
for end in range(len(array) - 1, 0, -1):
array[0], array[end] = array[end], array[0]
heap_adjust(array, 0, end - 1)
if __name__ == "__main__":
array = [1, 4, 5, 0, 2, 7, 9, 10, 3, 6]
heap_sort(array)
print(array)
[0, 1, 2, 3, 4, 5, 6, 7, 9, 10]
把序列拆分再合并起来,使用分治法来实现,这就意味要构造递归算法(分治法典型的应用)
时间复杂度
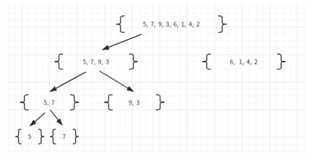
这个图明显是二叉树的形式,所以若集合有n个元素,那高度就为log(n),但其实在每一层做比较的时候,都是一个一个的向序列中放小的元素,每一层都要放n次,所以时间复杂度是nlog(n).
def merge(s1, s2, s):
"""将两个列表s1,s2按顺序融合为一个列表s,s为原列表"""
# j和i就相当于两个指向的位置,i指s1,j指s2
i = j = 0
while i+j<len(s):
# j==len(s2)时说明s2走完了,或者s1没走完并且s1中该位置是最小的
if j==len(s2) or (i<len(s1) and s1[i]<s2[j]):
s[i+j] = s1[i]
i += 1
else:
s[i+j] = s2[j]
j += 1
def merge_sort(s):
"""归并排序"""
n = len(s)
# 剩一个或没有直接返回,不用排序
if n < 2:
return
# 拆分
mid = n // 2
s1 = s[0:mid]
s2 = s[mid:n]
# 子序列递归调用排序
merge_sort(s1)
merge_sort(s2)
# 合并
merge(s1, s2, s)
if __name__== "__main__":
s = [1, 4, 56, 34, 12, 34, 59]
merge_sort(s)
print(s)
[1, 4, 12, 34, 34, 56, 59]
基数排序:通过序列中各个元素的值,对排序的N个元素进行若干趟的“分配”与“收集”来实现排序
希尔排序:按照步长gap进行分组,然后将每组的元素利用直接插入排序的方法进行排序;每次将gap折半减小,循环上述操作;当gap=1时,利用直接插入,完成排序.
标签:分组 数据 def 二叉树 说明 开始 hellip 高度 排序算法
原文地址:https://www.cnblogs.com/qingaoaoo/p/12350046.html