标签:之间 关于 启发式 最大 根据 拉格朗日对偶 函数 输出 选择
在SVM的前两篇里,我们优化的目标函数最终都是一个关于α向量的函数。而怎么极小化这个函数,求出对应的α向量,进而求出分离超平面我们没有讲。本篇就对优化这个关于α向量的函数的SMO算法做一个总结。
序列最小优化算法(Sequential minimal optimization, SMO)是一种用于解决SVM训练过程中所产生的优化问题的算法。 于1998年由John Platt发明。
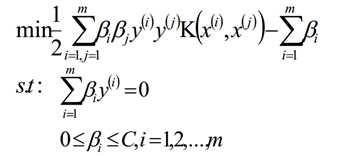
假定存在一个β*=(β1,β2,...,βm)是我们最终的最优解,那么根据KKT条件我们可以
计算出w和b的最优解,如下:
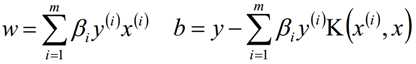
进而我们可以得到最终的分离超平面为:
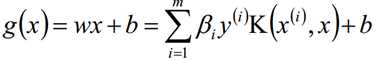
拉格朗日乘子法和KKT的对偶互补条件为:
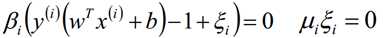
β、μ和C之间的关系为:
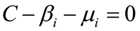
根据这个对偶互补条件,我们有如下关系式:
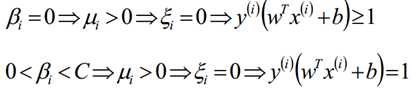
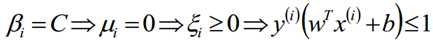
根据上式,我们得到以下式子,也就是说我们找出的最优的分割超平面必须满足下列的目标条件(g(x)):
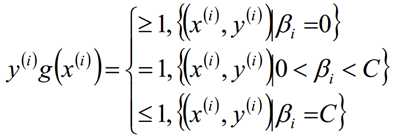
拉格朗日对偶化要求的两个限制的初始条件为:
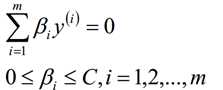
从而可以得到解决问题的思路如下:
备注:这个求解过程中,和传统的思路不太一样,不是对目标函数求最小值,而是让g(x)目标条件尽可能的满足。
上面优化式子比较复杂,里面有m个变量组成的向量β需要在目标函数极小化的时候求出。直接优化时很难的。利用启发式的方法/EM算法的思想,每次优化的时候,只优化两个变量,将其它的变量看成常数项,这样SMO算法就将一个复杂的优化算法转换为一个比较简单的两变量优化问题了。
整理可以发现β值的优化必须遵循以下两个基本原则:
为了后面表示方便,我们定义:
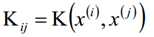
认为β1、β2是变量,其它β值是常量,从而将目标函数转换如下:
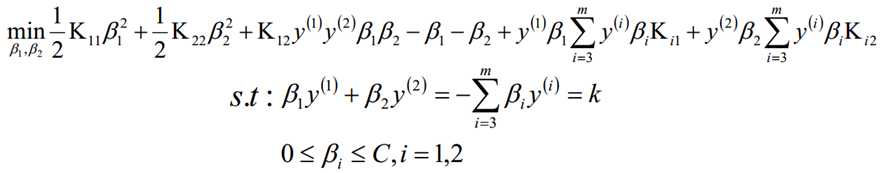

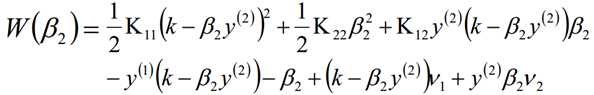
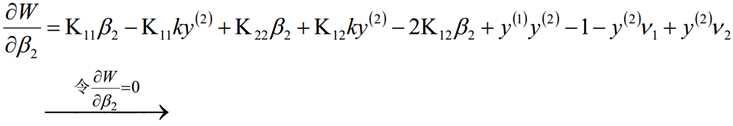
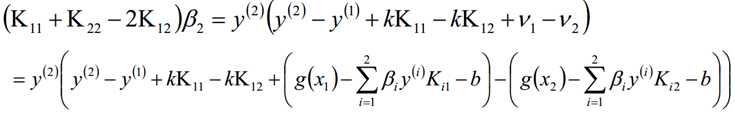
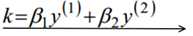
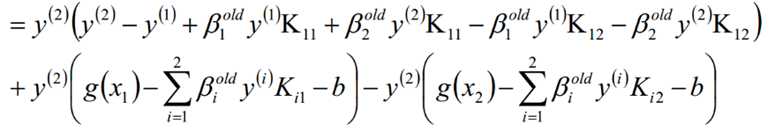
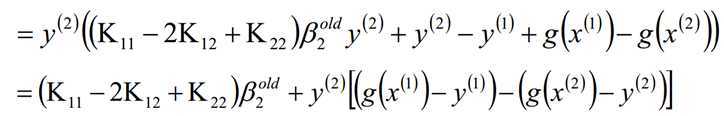
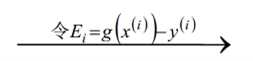
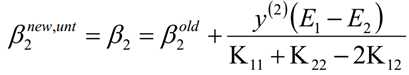
考虑β1和β2的取值限定范围,假定新求出来的β值是满足我们的边界限制的,即如下所示,可以通过看图,也可以通过代数计算得出:
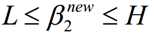
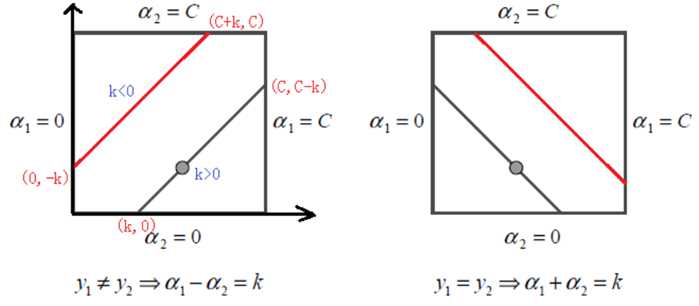
当y1≠y2的时候,β1-β2=k;由于β的限制条件,我们可以得到:
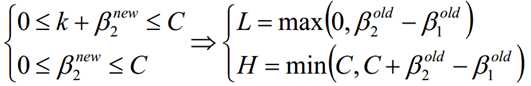
当y1=y2的时候,β1+β2=k; 由于β的限制条件,我们可以得到:
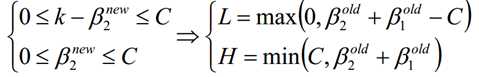
结合β的取值限制范围以及函数W的β最优解,我们可以得带迭代过程中的最优解为
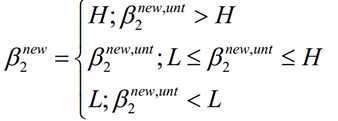
然后根据β1和β2的关系,从而可以得到迭代后的β1的值:
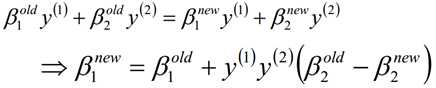
求解β的过程中,相关公式如下:
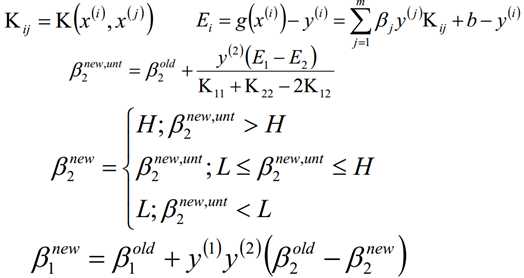
可以发现SMO算法中,是选择两个合适的β变量做迭代,其它变量作为常量来进行优化的一个过程,那么这两个变量到底怎么选择呢?
SMO算法在选择第一个β变量的时候,需要选择在训练集上违反KKT条件最严重的样本点。一般情况下,先选择0<β<C的样本点(即支持向量),只有当所有的支持向量都满足KKT条件的时候,才会选择其它样本点。因为此时违反KKT条件越严重,在经过一次优化后,会让变量β尽可能的发生变化,从而可以以更少的迭代次数让模型达到g(x)目标条件
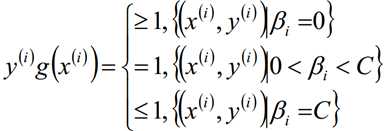
在选择第一个变量β1后,在选择第二个变量β2的时候,希望能够按照优化后的β1和β2有尽可能多的改变来选择,也就是说让|E1-E2|足够的大,当E1为正的时候,选择最小的Ei作为E2;当E1为负的时候,选择最大的Ei作为E2。
备注:如果选择的第二个变量不能够让目标函数有足够的下降,那么可以通过遍历所有样本点来作为β2,直到目标函数有足够的下降,如果都没有足够的下降的话,那么直接跳出循环,重新选择β1;
在每次完成两个β变量的优化更新之后,需要重新计算阈值b和差值Ei。
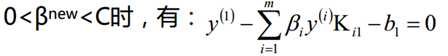
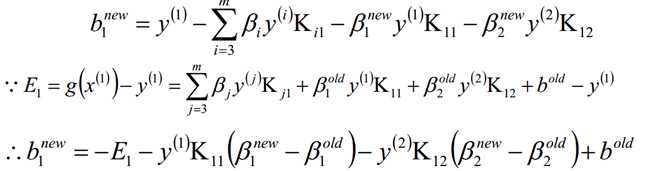
同样的当β2的取值为: 0<β2<C的时候,我们也可以得到
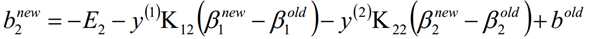
最终计算出来的b为:
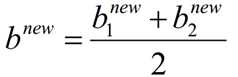
当更新计算阈值b后,就可以得到差值Ei为:
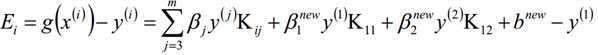
5.1、输入线性可分的m个样本数据{(x1,y1),(x2,y2),...,(xm,ym)},其中x为n维的特征向量,y为二元输出,取值为+1或者-1;精度为e


5.2、按照β1k和β2k的关系,求出β1k+1的值:
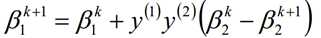
5.3、按照公式计算bk+1和Ei的值;
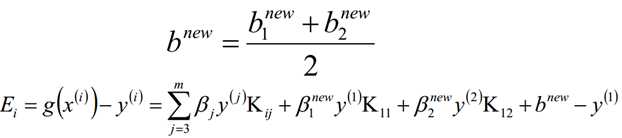
5.4、检查函数y(i)*Ei的绝对值是否在精度范围内,并且求解出来的β解满足KKT相关约束条件,那么此时结束循环,返回此时的β解即可,否则继续迭代计算β2new,unt的值。
? ?
? ?
? ?
? ?
标签:之间 关于 启发式 最大 根据 拉格朗日对偶 函数 输出 选择
原文地址:https://www.cnblogs.com/yifanrensheng/p/12354948.html