标签:取反 图片 连续 大小 元素 space str clu 思想
要求: 输入一个整形数组,数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
求所有子数组的和的最大值。要求时间复杂度为O(n)
以上就是对应的题目的要求:
对于不是环形数组的设计的思想就是:-----------------------------------
主要的是:
for(i=2;i<=n;i++) { if(a[i]+a[i-1]>a[i]) a[i]=a[i]+a[i-1]; } int ans=-100000; for(i=1;i<=n;i++) ans=max(ans,a[i]);
当前的数组中的一个元素加上他前边的一个元素。得到的和与刚才不想加的元素本身相比较。看看大小。如果求得和大于当当它本身。那就用和来替代它本身的数值。
依次进行此遍历。来取得多个子数组的最大值,这些最大值就被保存在数组中的某一个元素中了。
之后再进行依次遍历求出数组中的最大值来,就好了。
对于环形数组的设计思想:-------------------------------------------------------------
主要是:
#include<iostream> using namespace std; int main() { int a[100],b[100],i,n; cin>>n; for(i=1;i<=n;i++) { cin>>a[i]; } for(i=1;i<=n;i++) { b[i]=a[i]-2*a[i]; } int w=0; for(i=1;i<=n;i++) { w+=a[i]; } for(i=2;i<=n;i++) { if(a[i]+a[i-1]>a[i]) a[i]=a[i]+a[i-1]; } int ans=-100000; for(i=1;i<=n;i++) ans=max(ans,a[i]); for(i=2;i<=n;i++) { if(b[i]+b[i-1]>b[i]) b[i]=b[i]+b[i-1]; } int ans2=-100000; for(i=1;i<=n;i++) ans2=max(ans2,b[i]); int ans22=w+ans2; int wen=max(ans,ans22); cout<<wen<<endl; return 0; }
先将原来的数组取反并赋值给另外的一个数组。
对就数组进行求和处置。求出整个数组的和。
之后算出新数组中最小的子数组的和。
应用反向的思维。如果想求出最大的子数组的和。就是当先求出一个数组长度的最大子数组的和,与另外一个最大值进行比较取得最大值。
具体就是将整个案列分成了最大子数组的和在0~n之间还是在n之外。
对另外一个最大值,应用反向的思维,想要子数组最大,先求出子数组最小。之后用数组的总和减去最小子数组的值,就是另外的一个最大值。
之后两个最大值进行比较。
运行的结果如下:
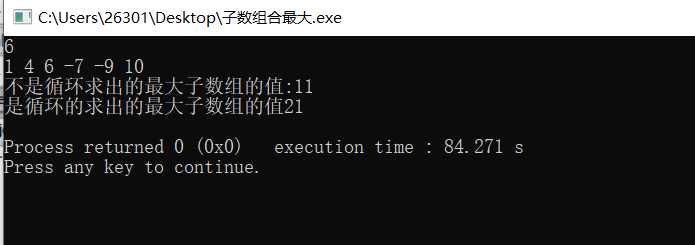
完整的代码如下:
#include<iostream> using namespace std; int main() { int a[100],b[100],i,n; cin>>n; for(i=1;i<=n;i++) { cin>>a[i]; } for(i=1;i<=n;i++) { b[i]=a[i]-2*a[i]; } int w=0; for(i=1;i<=n;i++) { w+=a[i]; } for(i=2;i<=n;i++) { if(a[i]+a[i-1]>a[i]) a[i]=a[i]+a[i-1]; } int ans=-100000; for(i=1;i<=n;i++) ans=max(ans,a[i]); for(i=2;i<=n;i++) { if(b[i]+b[i-1]>b[i]) b[i]=b[i]+b[i-1]; } int ans2=-100000; for(i=1;i<=n;i++) ans2=max(ans2,b[i]); int ans22=w+ans2; cout<<"不是循环求出的最大子数组的值:"<<ans<<endl; int wen=max(ans,ans22); cout<<"是循环的求出的最大子数组的值"<<wen<<endl; return 0; }
另外一种求循环数组中的最大子数组的值,就是直接求证。先将数组的n个数字收尾相连,化解成一个2n的一个不循环的数组。
这样通过刚刚求n个数组元素的时候的方法是一样的。但是要注意的是。一定要得到连续相加的两个开始时候的下表、还有就是结束时候的下表。
要防止两个下表相减之后的结果不能大于n。为了防止重复相加的情况存在。
返回一个整数数组中最大子数组的和(然后就是一个环形数组的相关的操作)
标签:取反 图片 连续 大小 元素 space str clu 思想
原文地址:https://www.cnblogs.com/dazhi151/p/12369514.html