标签:orm width @param 顺序 百度百科 部分 结果 static int
来源百度百科:
快速排序由C. A. R. Hoare在1962年提出。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序是面试出现的可能性比较高的,也是经常会用到的一种排序,应该重点掌握。
前面一个章节已经讲了递归了,那么现在来看快速排序就非常简单了。
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小
百度百科的话并没有说到重点,更简单的理解是这样的:在数组中找一个支点(任意),经过一趟排序后,支点左边的数都要比支点小,支点右边的数都要比支点大!
现在我们有一个数组:int arr[]={1,4,5,67,2,7,8,6,9,44};
经过一趟排序之后,如果我选择数组中间的数作为支点:7(任意的),那么第一趟排序后的结果是这样的:{1,4,5,6,2,7,8,67,9,44}
那么就实现了支点左边的数比支点小,支点右边的数比支点大
现在我们的数组是这样的:{1,4,5,6,2,7,8,67,9,44},既然我们比7小的在左边,比7大的在右边,那么我们只要将”左边“的排好顺序,又将”右边“的排好序,那整个数组是不是就有序了?想一想,是不是?
又回顾一下递归:”左边“的排好顺序,”右边“的排好序,跟我们第一趟排序的做法是不是一致的?
只不过是参数不一样:第一趟排序是任选了一个支点,比支点小的在左边,比支点大的在右边。那么,我们想要”左边“的排好顺序,只要在”左边“部分找一个支点,比支点小的在左边,比支点大的在右边。
..............
在数组中使用递归依照我的惯性,往往定义两个变量:L和R,L指向第一个数组元素,R指向在最后一个数组元素
递归出口也很容易找到:如果数组只有一个元素时,那么就不用排序了
所以,我们可以写出这样的代码:
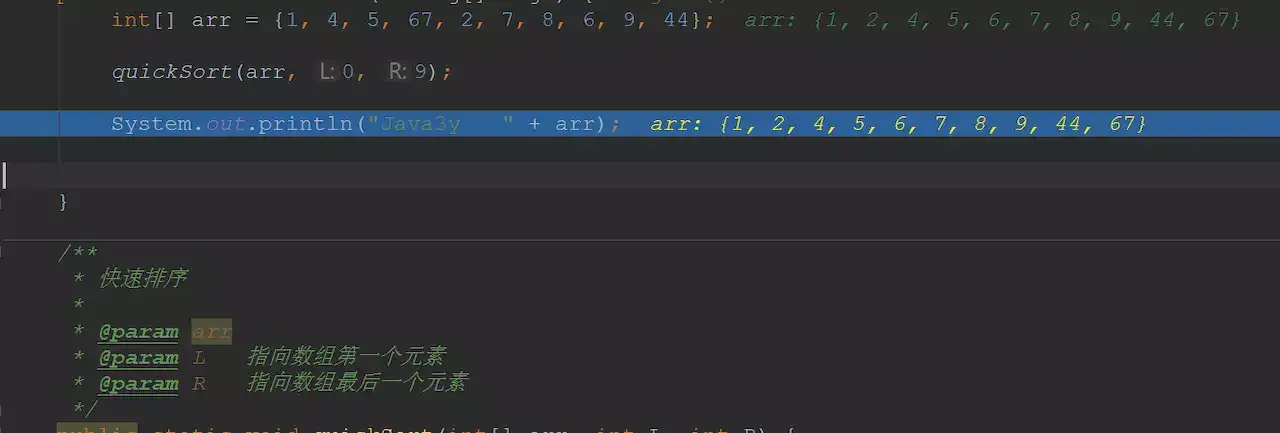
1 public static void main(String[] args) { 2 int[] arr = {1, 4, 5, 67, 2, 7, 8, 6, 9, 44}; 3 4 quickSort(arr, 0, 9); 5 6 System.out.println("Java3y " + arr); 7 8 9 } 10 11 /** 12 * 快速排序 13 * 14 * @param arr 15 * @param L 指向数组第一个元素 16 * @param R 指向数组最后一个元素 17 */ 18 public static void quickSort(int[] arr, int L, int R) { 19 int i = L; 20 int j = R; 21 22 //支点 23 int pivot = arr[(L + R) / 2]; 24 25 //左右两端进行扫描,只要两端还没有交替,就一直扫描 26 while (i <= j) { 27 28 //寻找直到比支点大的数 29 while (pivot > arr[i]) 30 i++; 31 32 //寻找直到比支点小的数 33 while (pivot < arr[j]) 34 j--; 35 36 //此时已经分别找到了比支点小的数(右边)、比支点大的数(左边),它们进行交换 37 if (i <= j) { 38 int temp = arr[i]; 39 arr[i] = arr[j]; 40 arr[j] = temp; 41 i++; 42 j--; 43 } 44 } 45 //上面一个while保证了第一趟排序支点的左边比支点小,支点的右边比支点大了。 46 47 48 //“左边”再做排序,直到左边剩下一个数(递归出口) 49 if (L < j) 50 quickSort(arr, L, j); 51 52 //“右边”再做排序,直到右边剩下一个数(递归出口) 53 if (i < R) 54 quickSort(arr, i, R); 55 } 56
标签:orm width @param 顺序 百度百科 部分 结果 static int
原文地址:https://www.cnblogs.com/xujiangxi/p/12374773.html