树状数组

标签：info   size   操作   答案   倒序   alt   http   style   log   

# 支持的操作

1）快速求前缀和 O(log n)

2) 修改某一个数 O(logn)

# 原理

原数组的长度为x的话，x的二进制为(下标从 1 开始)

x = 2ⁱ¹+2ⁱ²+2ⁱ³+.......+2^im 

那么按照x的二进制可以讲区间划分为 log x 个区间。分别为

[ x-2ⁱ¹⁺¹ +1 , x ] , 区间长度为2ⁱ¹

[ x-2ⁱ¹ -2ⁱ² +1 , x -2ⁱ¹ ] , 区间长度为2ⁱ²

[ x-2ⁱ¹ -2ⁱ² -2ⁱ³ +1 , x -2ⁱ¹ -2ⁱ²] , 区间长度为2ⁱ³

......

[ x-2ⁱ¹ -2ⁱ² -2ⁱ³ ......-2^im + 1 , x -2ⁱ¹ -2ⁱ² -......-2^i[m-1]] , 区间长度为2^im

a数组是原数组,c数组是求和后的数组，

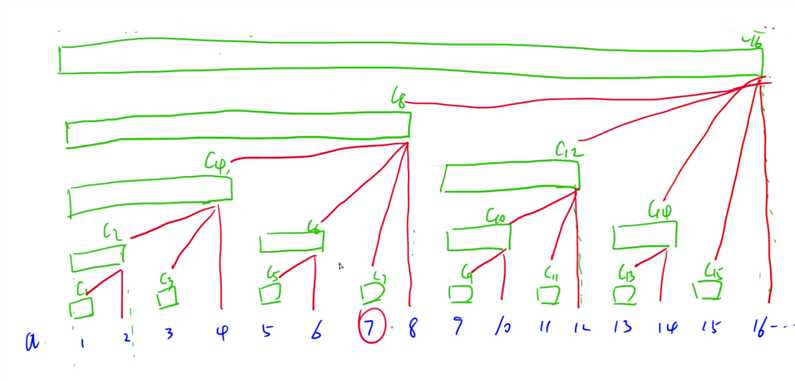
查询操作，如图，2的倍数的lowbit是其本身，其他的一直算即可

单点增加运算通过lowbit算其父节点，通过+lowbit（x）就能知道其父节点。

在执行所有操作之前需要对树状数组进行初始化  

# 树状数组求逆序对

在a的数值范围上面建立一个树状数组，树状数组统计的前缀和是点的个数。

步骤：
1）查询前缀和 [ 1 , a[i]-1 ]，并累加到答案中

2）执行单点增加操作，即将 a[i] 数值在树状数组中+1，维护前缀和，这表示数值 a[i] 出现了一次

3）ans就是所有的逆序对

因为是倒序扫描，已经出现的数就是在 a[i] 后面的数，所以查询的是在 i 后面，小于a[i]的数值个数有多少个

时间复杂度为O ( (N + M) log M) , M为数值范围的大小。

查询的复杂度为O（M * log M）

加入的复杂度为O（N * logM）

树状数组

标签：info   size   操作   答案   倒序   alt   http   style   log   

原文地址：https://www.cnblogs.com/hhyx/p/12375343.html