最小编辑距离python

标签：size   多少   range   png   步骤   return   image   com   问题   

1 什么是编辑距离
在计算文本的相似性时，经常会用到编辑距离（Levenshtein距离），其指两个字符串之间，由一个字符串转成另一个所需的最少编辑操作次数。在字符串形式上来说，编辑距离越小，那么两个文本的相似性越大，暂时不考虑语义上的问题。其中，编辑操作包括以下三种：

插入：将一个字符插入某个字符串
删除：将字符串中的某个字符删除
替换：将字符串中的某个字符串替换为另一个字符
为了更好地说明编辑距离的概念，我们看看一个例子，将字符串“batyu”变为“beauty”，编辑距离是多少呢？分析步骤如下：

将batyu插入字符e有：beatyu
将beatyu删除字符u有：beaty
将beaty插入字符u有：beauty
所以，字符串“batyu”与字符串“beauty”之间的编辑距离为：3.

2 数学化
先抛开具体编程语言实现，我们简单地分析一下如何计算两个字符串之间的编辑距离

当两个字符串都为空串的时候，那么编辑距离就是0
当其中一个字符串为空串时，那么编辑距离为另一个非空字符串的长度
当两个字符串A,B均为非空时(假设长度分别为i,j)，那么有如下三种情况，我们取这三种情况的最小值即可：
1). 已知字符串A中长为 i - 1(从字符串首开始，以下描述字符串长默认此种描述)和字符串B长为j的编辑距离，那么在此基础上加1即可
2).长度分别为i,h和j-1的编辑距离已知，那么加1即可
3).长度分别为i-1和j-1的编辑距离已知，这个时候需要考虑两种情况，若第i个字符和第j个字符不同，那么加1即可，如果相同，那么就不需要加1.
从上面的描述，很明显可以发现是动态规划的思想。
我们将上面的叙述数学化，则有：求长度为m和n的字符A、B串编辑距离，即函数：edit(i,j),它表示第一个长度为i(从字符首开始)的字符串与第二个长度为j的字符串之间的编辑距离。动态规划表达式则有如下写法，假设i,j表示字符串A,B的字串长度：

if i==0 且 j==0,edit(i,j)=0
if (i==0 且 j>0) 或者(i>0 且j ==0)，edit(i,j)=i + j
if i>= 1 且 j >= i, edit(i, j) = min(edit(i-1,j) + 1, edit(i, j-1) + 1, edit(i-1,j-1) + d(i,j);当第一个字符串的第i个字符不等于第二个字符串第j个字符时，d(i,j)=1，否则为0
字符串“batyu”与字符串“beauty”之间的编辑距离矩阵则有如下表示：

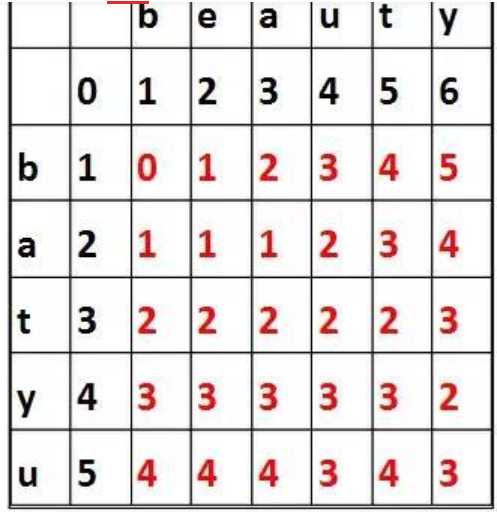
最终的编辑距离即为edit(m,n)。

3 编程实现
有了上面的思路，使用Python去实现计算两个字符串的编辑距离就简单多了。

def test(s1,s2):
    edit = [[i+j for j in range(len(s2)+1)] for i in range(len(s1)+1)]

    for i in range(1,len(s1)+1):
        for j in range(1,len(s2)+1):
            if s1[i-1]==s2[j-1]:
                d=0
            else:
                d=1
            edit[i][j] = min(edit[i-1][j]+1,edit[i][j-1]+1,edit[i-1][j-1]+d)
    return edit[len(s1)][len(s2)]
t = test(‘batyu‘,‘beauty‘)
print(t)

最小编辑距离python

标签：size   多少   range   png   步骤   return   image   com   问题   

原文地址：https://www.cnblogs.com/limingqi/p/12376729.html