标签:mod 这一 image 全连接 nump shape ram jpg 通道数
LeNet-5是一个简单的卷积神经网络,是用于手写字体的识别的一个经典CNN
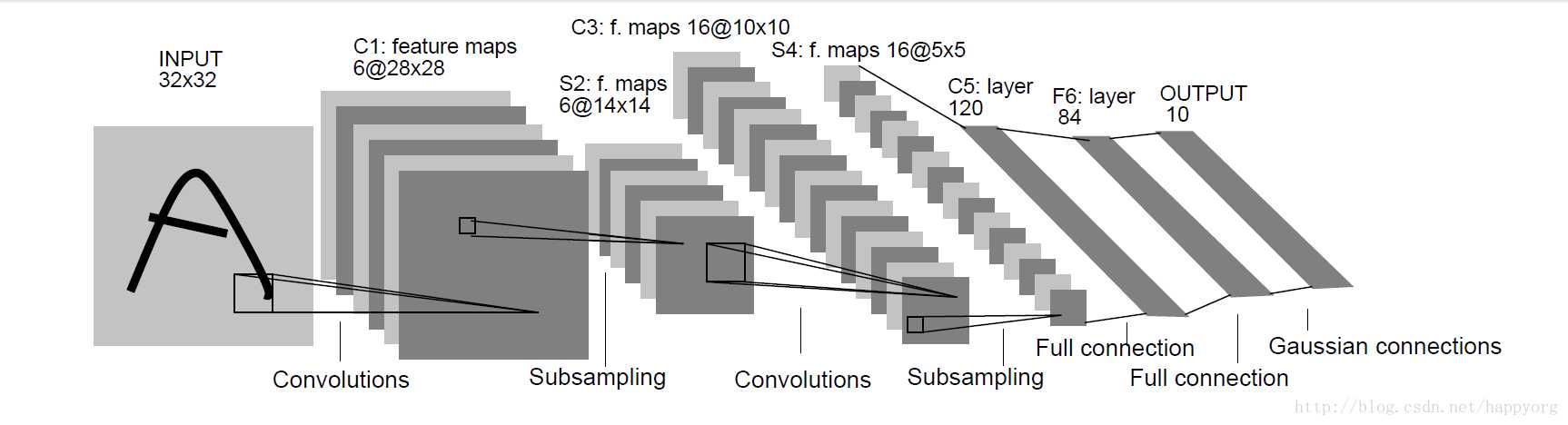
前向传播过程如下:
INPUT层
这是神经网络的输入,输入图像的尺寸统一为32×32。
C1层
输入图片:32×32
卷积核大小:5×5
卷积核种类:6
输出feature map大小:28×28
神经元数量:28×28×6
可训练参数:(5×5+1) × 6(每个滤波器5×5=25个参数和一个bias参数,一共6个滤波器)
S2层
输入:28×28
采样区域:2×2
采样种类:6
输出feature Map大小:14×14(28/2)
神经元数量:14×14×6
C3层
输入:14×14×6
卷积核大小:5×5
卷积核种类:16
输出feature Map大小:10×10 ((14-5+1)=10)
S4层
输入:10×10
采样区域:2×2
采样种类:16
输出feature Map大小:5×5(10/2)
神经元数量:5×5×16=400
C5层
输入:S4层的全部16个单元特征map(与s4全相连)
卷积核大小:5×5
卷积核种类:120
输出feature Map大小:1×1(5-5+1)
F6层
输入:c5 120维向量
计算方式:计算输入向量和权重向量之间的点积,再加上一个偏置,结果通过sigmoid函数输出。
有84个神经元
可训练参数:84×(120+1)=10164
OUTPUT层
Output层也是全连接层,共有10个神经元,分别代表数字0到9,且如果节点i的值为0,则网络识别的结果是数字i
import numpy as np import tensorflow as tf from tensorflow.python.framework import graph_util from PIL import Image import os ‘‘‘构建数据集‘‘‘ # 第一次遍历图片目录是为了获取图片总数 input_count = 0 for i in range(0, 10): dir = ‘./mnist_digits_images/%s/‘ % i # 这里可以改成你自己的图片目录,i为分类标签 for rt, dirs, files in os.walk(dir): for filename in files: input_count += 1 # 定义对应维数和各维长度的数组 input_images = np.array([[0] * 1024 for i in range(input_count)]) input_labels = np.array([[0] * 10 for i in range(input_count)]) # 第二次遍历图片目录是为了生成图片数据和标签 index = 0 for i in range(0, 10): dir = ‘./mnist_digits_images/%s/‘ % i # 这里可以改成你自己的图片目录,i为分类标签 for rt, dirs, files in os.walk(dir): for filename in files: filename = dir + filename img = Image.open(filename) width = img.size[0] height = img.size[1] for h in range(0, height): for w in range(0, width): # 通过这样的处理,使数字的线条变细,有利于提高识别准确率 if img.getpixel((w, h)) > 230: input_images[index][w + h * width] = 0 # 之前已经将图片转换成了一维 else: input_images[index][w + h * width] = 1 input_labels[index][i] = 1 index += 1 ‘‘‘定义占位符‘‘‘ # 定义输入节点,对应于图片像素值矩阵集合和图片标签(即所代表的数字) x = tf.placeholder(tf.float32, shape=[None, 1024]) y_ = tf.placeholder(tf.float32, shape=[None, 10]) x_image = tf.reshape(x, [-1, 32, 32, 1]) ‘‘‘定义权重和偏置‘‘‘ ‘‘‘ 输入矩阵格式:四个维度,依次为:样本数、图像高度、图像宽度、图像通道数 输出矩阵格式:与输出矩阵的维度顺序和含义相同,但是后三个维度(图像高度、图像宽度、图像通道数)的尺寸发生变化。 权重矩阵(卷积核)格式:同样是四个维度,但维度的含义与上面两者都不同,为:卷积核高度、卷积核宽度、输入通道数、输出通道数(卷积核个数) 输入矩阵、权重矩阵、输出矩阵这三者之间的相互决定关系 卷积核的输入通道数(in depth)由输入矩阵的通道数所决定。(红色标注) 输出矩阵的通道数(out depth)由卷积核的输出通道数所决定。(绿色标注) 输出矩阵的高度和宽度(height, width)这两个维度的尺寸由输入矩阵、卷积核、扫描方式所共同决定。计算公式如下。(蓝色标注) ‘‘‘ ‘‘‘构建网络‘‘‘ # 构建第1个卷积层 W_conv1 = tf.Variable(tf.truncated_normal([5, 5, 1, 6], stddev=0.1)) # 定义卷积核 b_conv1 = tf.Variable(tf.constant(0.1, shape=[6])) # 定义偏置 L1_conv = tf.nn.conv2d(x_image, W_conv1, strides=[1, 1, 1, 1], padding=‘VALID‘) # 进行卷积操作 L1_relu = tf.nn.relu(L1_conv + b_conv1) # 通过激活函数 L1_pool = tf.nn.max_pool(L1_relu, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding=‘VALID‘) # 进行池化操作 # 构建第2个卷积层 W_conv2 = tf.Variable(tf.truncated_normal([5, 5, 6, 16], stddev=0.1)) # 定义卷积核 b_conv2 = tf.Variable(tf.constant(0.1, shape=[16])) # 定义偏置 L2_conv = tf.nn.conv2d(L1_pool, W_conv2, strides=[1, 1, 1, 1], padding=‘VALID‘) # 进行卷积操作 L2_relu = tf.nn.relu(L2_conv + b_conv2) # 通过激活函数 L2_pool = tf.nn.max_pool(L2_relu, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding=‘VALID‘) # 进行池化操作 # 构建第1个全连接层 W_fc1 = tf.Variable(tf.truncated_normal([5 * 5 * 16, 120], stddev=0.1)) b_fc1 = tf.Variable(tf.constant(0.1, shape=[120])) h_pool2_flat = tf.reshape(L2_pool, [-1, 5 * 5 * 16]) h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1) # 构建第2个全连接层 W_fc2 = tf.Variable(tf.truncated_normal([120, 84], stddev=0.1)) b_fc2 = tf.Variable(tf.constant(0.1, shape=[84])) h_fc2 = tf.nn.relu(tf.matmul(h_fc1, W_fc2) + b_fc2) # 构建output层 W_out = tf.Variable(tf.truncated_normal([84, 10], stddev=0.1)) b_out = tf.Variable(tf.constant(0.1, shape=[10])) y_conv = tf.matmul(h_fc2, W_out) + b_out pred = tf.nn.softmax(y_conv, name=‘out_softmax‘) #[n, 10] # 定义损失函数 cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y_conv)) # 运用梯度下降算法减小损失,学习率设置为0.0001 train_step = tf.train.AdamOptimizer((1e-4)).minimize(cross_entropy) # 将预测值与真实值的比较结果存放在一个布尔型列表中, correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1)) # 计算这一批次的准确率 accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) with tf.Session() as sess: # 初始化所有变量 sess.run(tf.global_variables_initializer()) print("一共读取了 %s 个输入图像, %s 个标签" % (input_count, input_count)) # 设置每次训练op的输入个数和迭代次数,这里为了支持任意图片总数,定义了一个余数remainder,譬如,如果每次训练op的输入个数为60,图片总数为150张,则前面两次各输入60张,最后一次输入30张(余数30) batch_size = 60 iterations = 500 batches_count = int(input_count / batch_size) remainder = input_count % batch_size print("数据集分成 %s 批, 前面每批 %s 个数据,最后一批 %s 个数据" % (batches_count + 1, batch_size, remainder)) # 执行训练迭代 for it in range(iterations): # 这里的关键是要把输入数组转为np.array for n in range(batches_count): aa = input_images[n * batch_size:(n + 1) * batch_size] train_step.run(feed_dict={x: input_images[n * batch_size:(n + 1) * batch_size], y_: input_labels[n * batch_size:(n + 1) * batch_size]}) if remainder > 0: start_index = batches_count * batch_size; train_step.run( feed_dict={x: input_images[start_index:input_count - 1], y_: input_labels[start_index:input_count - 1]}) # 保存模型 constant_graph = graph_util.convert_variables_to_constants(sess, sess.graph_def, ["out_softmax"]) # out_softmax with tf.gfile.FastGFile("model.pb", mode=‘wb‘) as f: f.write(constant_graph.SerializeToString()) # 每完成五次迭代,判断准确度是否已达到100%,达到则退出迭代循环 iterate_accuracy = 0 if it % 5 == 0: iterate_accuracy = accuracy.eval(feed_dict={x: input_images, y_: input_labels}) print(‘iteration %d: accuracy %s‘ % (it, iterate_accuracy)) if iterate_accuracy >= 1: break; print(‘完成训练!‘)
注意:如果想要用opencv进行调用pb模型,输入参数只能有一个,也就是placeholder的输入只能有一个,一般keep_prob的参数也需要是placeholder,试了一下产出的模型,opencv不能进行调用,暂时还没找到解决办法,只好将placeholder只保留一个。
import cv2 import numpy as np inference_pb = "model.pb" net = cv2.dnn.readNetFromTensorflow(inference_pb) frame = cv2.imread("0.jpg", 0) net.setInput(cv2.dnn.blobFromImage(frame, size=(32, 32), swapRB=True, crop=False)) cvOut = net.forward() print(cvOut) cvOut = np.argmax(cvOut[0]) print(cvOut) cv2.imshow("a", frame) cv2.waitKey(-1)
Tensorflow实现LeNet5网络并保存pb模型,实现自定义的手写数字识别(附opencv-python调用代码)
标签:mod 这一 image 全连接 nump shape ram jpg 通道数
原文地址:https://www.cnblogs.com/answerThe/p/12398209.html